Verifikationsbeispiele
Die Statik-Software von Dlubal liefert nachvollziehbare statische Berechnungen. Sie hat keinen "Black Box"-Charakter. Die hier zugänglichen Verifikationsbeispiele verdeutlichen dies und legen die Berechnungsmethoden offen.
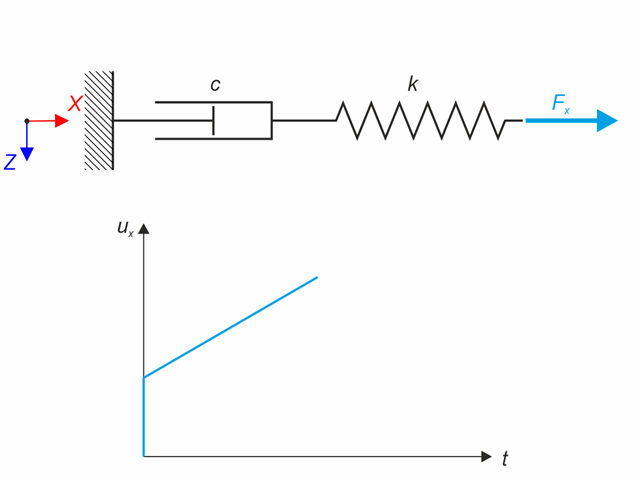
Das Maxwell-Materialmodell besteht aus einer in Reihe geschalteten linearen Feder und eines viskosen Dämpfers. In diesem Verifikationsbeispiel wird das Zeitverhalten dieses Modells getestet. Das Maxwell-Materialmodell wird durch eine konstante Kraft Fx belastet. Diese Kraft bewirkt dank der Feder eine Anfangsverformung, die dann aufgrund des Dämpfers mit der Zeit wächst. Die Verformung wird zum Zeitpunkt der Belastung (20 s) und am Ende der Analyse (120 s) untersucht. Zeitverlaufsanalyse mit der linearen impliziten Newmark-Methode.
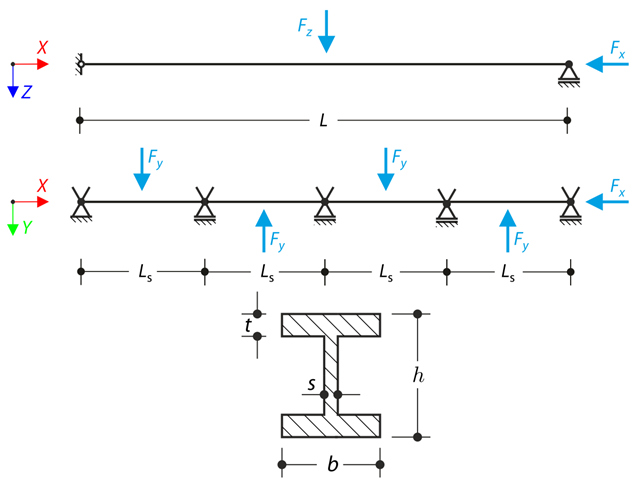
Durchlaufträger mit vier Feldern wird durch Normal- und Biegekräfte (Ersatz von Imperfektionen) belastet. Alle Auflager sind gabelgelagert - Wölbung ist frei. Es sollen die Verschiebungen uy und uz, Momente My, Mz, Mω und MTpri und die Verdrehung φx bestimmt werden. Dieses Verifikationsbeispiel basiert auf dem von Gensichen und Lumpe vorgestellten Beispiel.
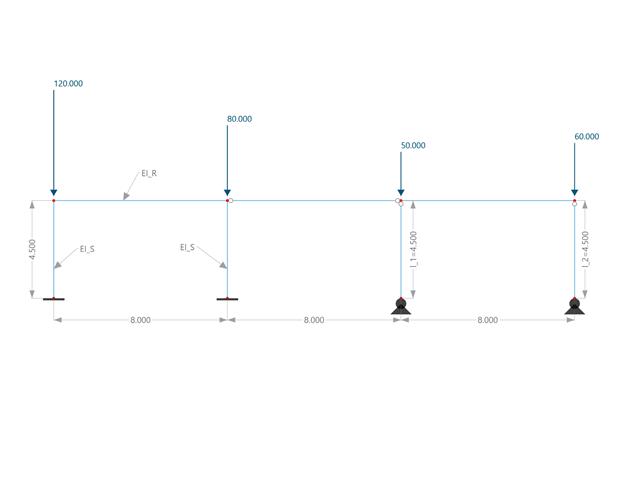
In diesem Beispiel werden die Knicklängen und der Verzweigungslastfaktor, welche in RFEM 6 mithilfe des Add-Ons Strukturstabilität berechnet werden können, mit einer Handrechnung verglichen. Als statisches System wird ein eingespannter Rahmen mit zwei zusätzlichen Pendelstützen betrachtet. Dieser ist durch vertikale Einzellasten belastet.
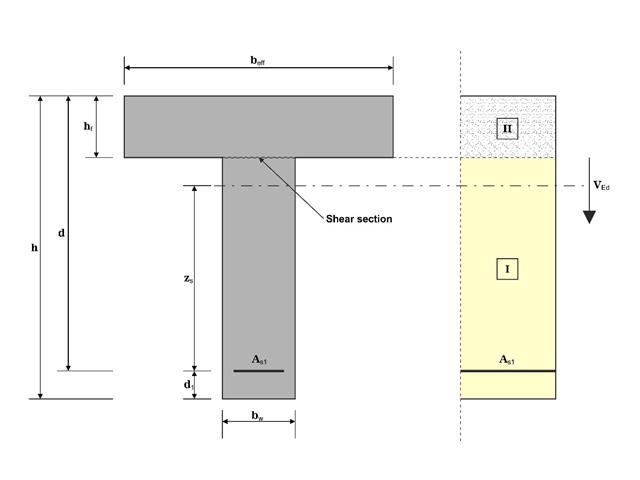
In diesem Beispiel werden die Schubkräfte an der Schnittstelle zwischen Beton zu unterschiedlichen Zeitpunkten und der zugehörigen Bewehrung nach DIN EN 1992-1-1 ermittelt. Die mit RFEM 6 erhaltenen Ergebnisse werden im Folgenden mit der Handberechnung verglichen.
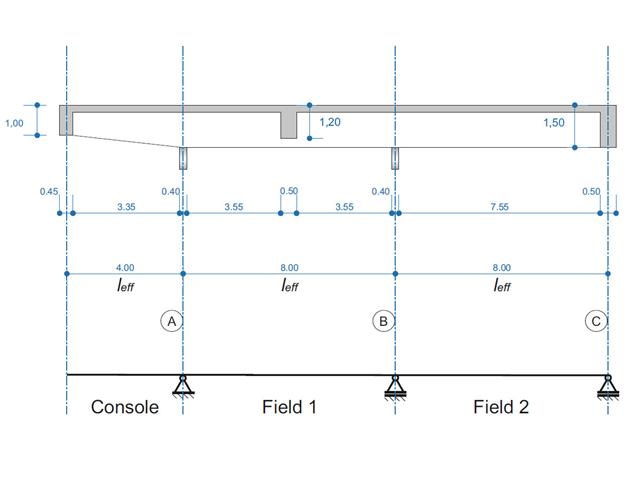
Ein Stahlbetonträger wird als Zweifeldträger mit Kragarm ausgeführt. Der Querschnitt variiert über die Länge des Kragarms (gevouteter Querschnitt). Es werden die Schnittgrößen, die erforderliche Längs- und Bügelbewehrung für den Grenzzustand der Tragfähigkeit berechnet.
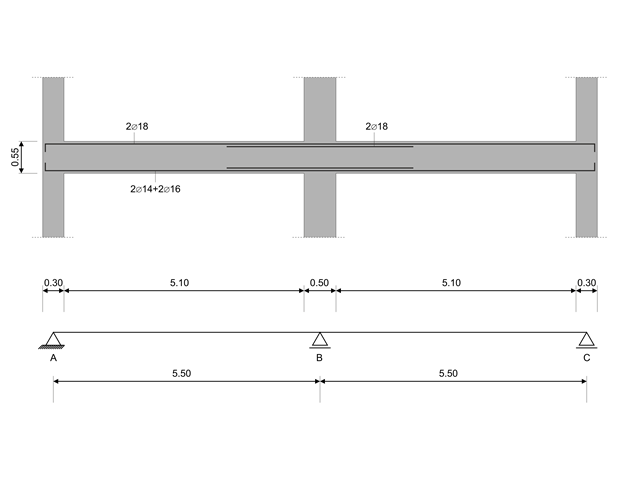
In diesem Verifikationsbeispiel werden die Kapazitätsbemessungswerte von Querkräften in Balken gemäß EN 1998-1, 5.4.2.2 und 5.5.2.1 sowie die Kapazitätsbemessungswerte von Stützen bei Biegung gemäß 5.2.3.3(2) berechnet. Das System besteht aus einem zweifeldrigen Stahlbetonträger mit einer Spannweite von 5,50 m. Der Träger ist Teil eines Rahmensystems. Die erhaltenen Ergebnisse werden mit denen in [1] verglichen.
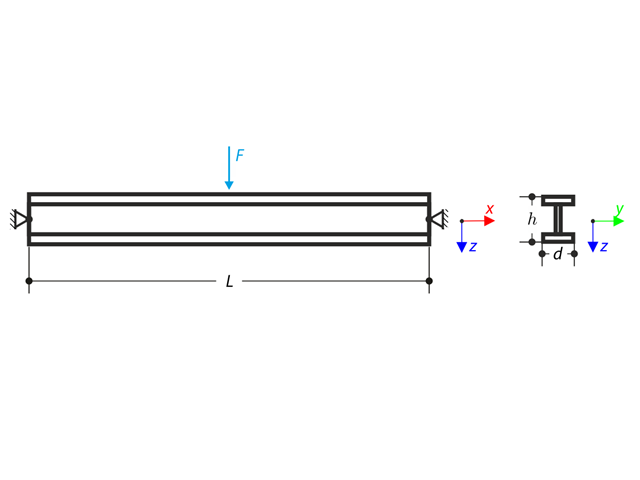
Die axiale Drehung des I-Profils wird an beiden Enden mittels der Gabellagerungen eingeschränkt (Verwölbung wird nicht behindert). Das Tragwerk wird in seiner Mitte durch zwei Querkräfte belastet. Das Eigengewicht wird in diesem Beispiel nicht berücksichtigt. Es sollen die maximalen Durchbiegungen des Tragwerks uy,max und uz,max, die maximale Verdrehung φx,max, die maximalen Biegemomente My,max und Mz,max und die maximalen Torsionsmomente MT,max, MTpri,max bestimmt werden. MTsec,max und Mω,max. Dieses Verifikationsbeispiel basiert auf dem von Gensichen und Lumpe vorgestellten Beispiel.
Ein Stab mit den festgelegten Randbedingungen wird durch Torsionsmoment und Normalkraft belastet. Unter Vernachlässigung seines Eigengewichts bestimmen Sie die maximale Torsionsverformung des Trägers' sowie sein inneres Torsionsmoment, das als Summe eines primären Torsionsmoments und eines durch die Normalkraft verursachten Torsionsmoments definiert ist. Vergleichen Sie diese Werte, während Sie den Einfluss der Normalkraft annehmen oder nicht berücksichtigen. Dieses Verifikationsbeispiel basiert auf dem von Gensichen und Lumpe vorgestellten Beispiel.
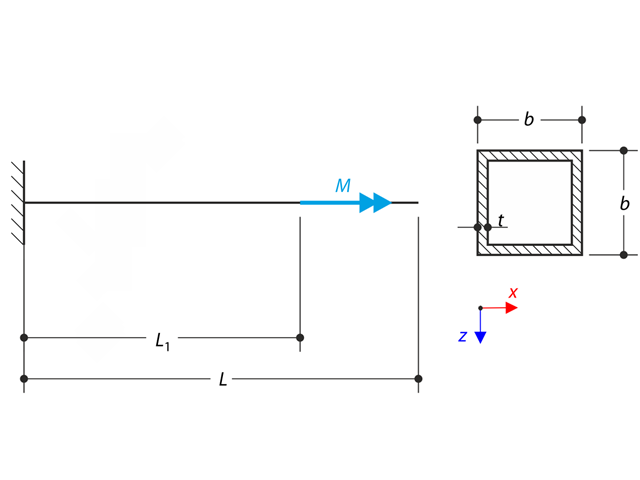
Ein Kragarm wird an seinem freien Ende durch ein Moment belastet. Unter Verwendung der geometrisch-linearen Analyse und der Theorie III. Ordnung und unter Vernachlässigung des Eigengewichts des Trägers' sind die maximalen Durchbiegungen am freien Ende zu bestimmen. Dieses Verifikationsbeispiel basiert auf dem von Gensichen und Lumpe vorgestellten Beispiel.
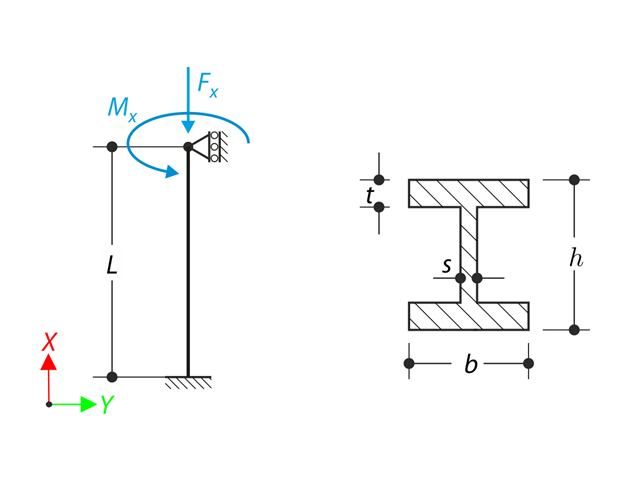
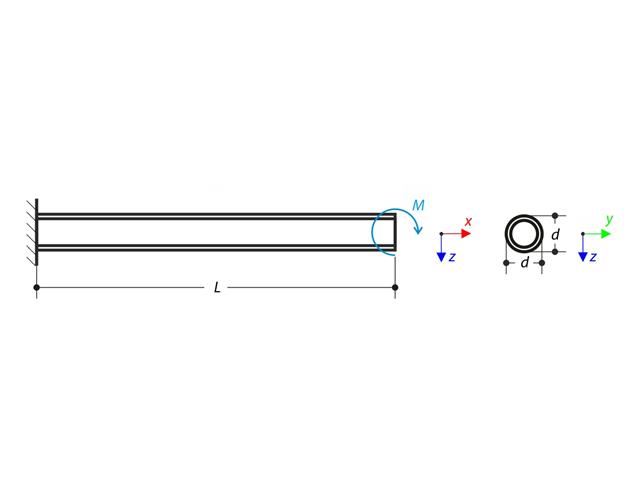
Ein dünnwandiger Kragträger aus einem QRO-Profil ist am linken Ende vollständig befestigt und wölbfrei. Der Kragarm wird einem Drehmoment ausgesetzt. Es werden kleine Verformungen berücksichtigt und das Eigengewicht wird vernachlässigt. Bestimmen Sie die maximale Verdrehung, primäres Moment, sekundäres Moment sowie Wölbmoment. Dieses Verifikationsbeispiel basiert auf dem von Gensichen und Lumpe vorgestellten Beispiel.
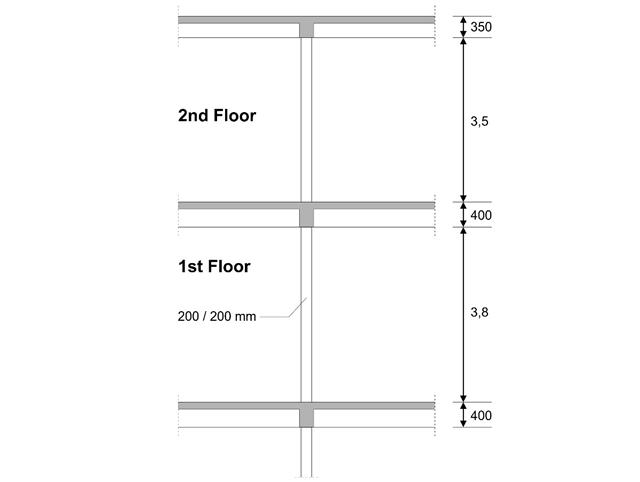
Bemessen wird eine Innenstütze im Erdgeschoss eines dreigeschossigen Gebäudes. Die Stütze ist monolithisch mit dem oberen und unteren Träger verbunden. Das vereinfachte Brandbemessungsverfahren A für Stützen nach EC2-1-2 wird dann geprüft und die Ergebnisse mit [1] verglichen.
Ein Träger ist am linken Ende vollständig fixiert (behinderte Wölbung) und am rechten Ende durch eine Gabelstütze (freie Wölbung) gelagert. Der Träger wird einem Drehmoment, einer Längskraft und einer Querkraft ausgesetzt. Bestimmen Sie das Verhalten des primären Torsionsmomentes, sekundären Torsionsmomentes und des Wölbmomentes. Das Verifikationsbeispiel basiert auf dem von Gensichen und Lumpe vorgestellten Beispiel (siehe Referenz).
Ein Kragträger mit I-Profil ist am linken Ende gelagert und wird durch das Drehmoment M belastet. Ziel dieses Beispiels ist es, das feste Lager mit dem Gabellager zu vergleichen und das Verhalten einiger repräsentativer Größen zu untersuchen. Der Vergleich mit der Lösung mittels Platten wird ebenfalls durchgeführt. Dieses Verifikationsbeispiel basiert auf dem von Gensichen und Lumpe vorgestellten Beispiel.
Eine Struktur aus Stäben mit I-Profilen wird an beiden Enden durch gleitende Federstützen gelagert und durch Transversalkräfte belastet. Das Eigengewicht wird in diesem Beispiel nicht berücksichtigt. Es soll die Durchbiegung des Systems, das Biegemoment, die Normalkraft in den festgelegten Prüfpunkten sowie die horizontale Auslenkung der Federlager bestimmt werden.
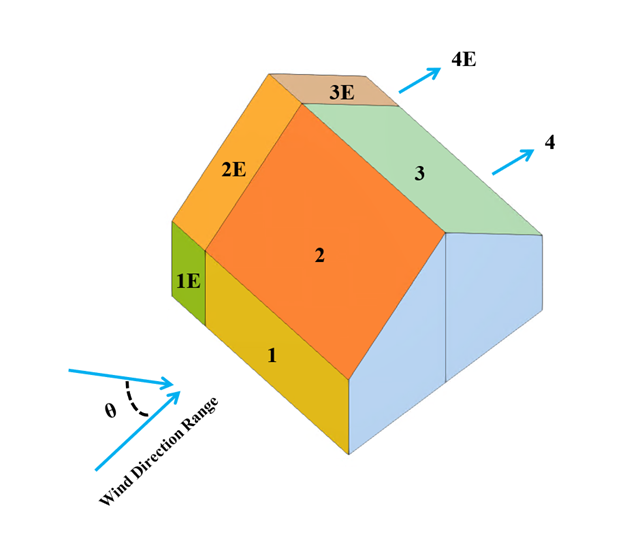
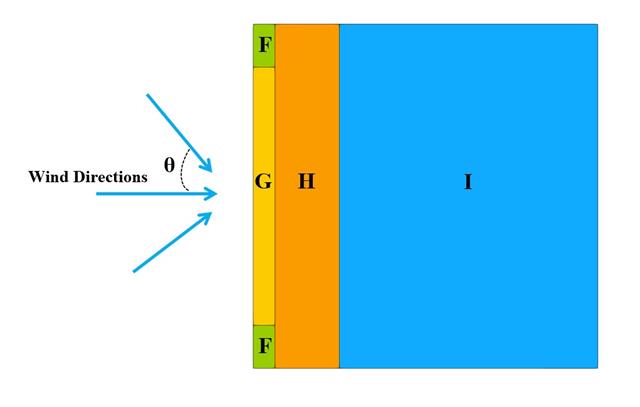
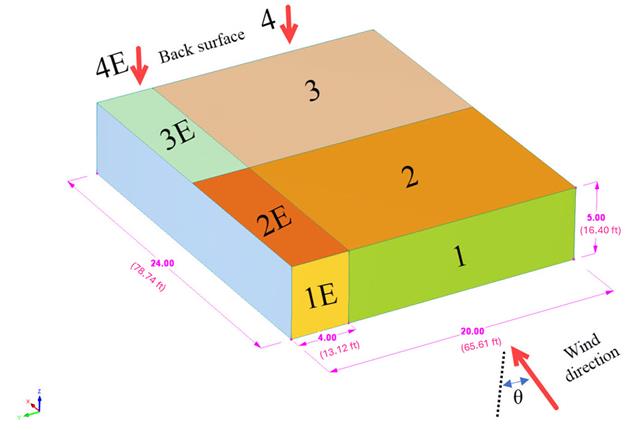
Im aktuellen Validierungsbeispiel wird der Winddruckbeiwert (Cp) sowohl für Hauptbauteile (Cp,ave ) als auch für Nebenbauteile wie Verkleidungen oder Fassadensysteme (Cp,lokal ) basierend auf NBC 2020 Siehe [1] and Japanische Windkanal-Datenbank für niedrige Gebäude mit einer Neigung von 45 Grad. Die empfohlene Einstellung für ein dreidimensionales Flachdach mit spitz zulaufender Traufe wird im nächsten Teil beschrieben.
Eine Struktur aus I-Profil ist am linken Ende vollständig fixiert und am rechten Ende in die Gleitlagerung eingebettet. Die Struktur besteht aus zwei Segmenten. Das Eigengewicht wird in diesem Beispiel nicht berücksichtigt. Es soll die maximale Durchbiegung des Tragwerks uz,max, das Biegemoment My am festen Ende, die Verdrehung σ2,y des Segments 2 und die Reaktionskraft RBz mittels Theorie I. Ordnung und Theorie II. Ordnung bestimmt. Dieses Verifikationsbeispiel basiert auf dem von Gensichen und Lumpe vorgestellten Beispiel.
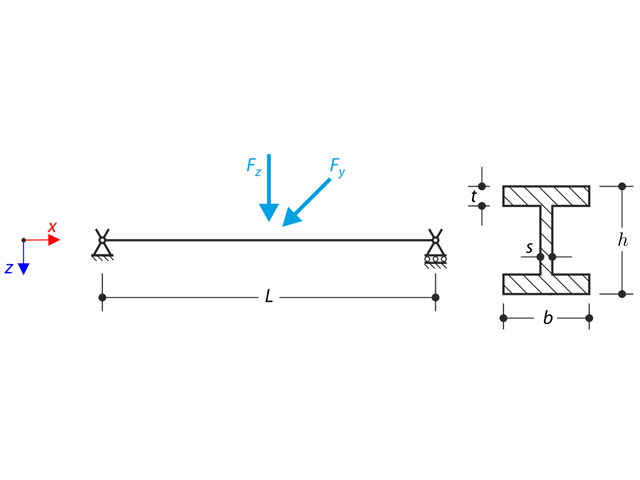
Der an beiden Enden gelenkige Träger wird in der Mitte mit der Querkraft belastet. Unter Vernachlässigung des Eigengewichts und der Schubsteifigkeit bestimmen Sie die maximale Durchbiegung, Normalkraft und das maximale Moment in Feldmitte unter Annahme der Theorie II. und III. Ordnung. Das Verifikationsbeispiel basiert auf dem von Gensichen und Lumpe vorgestellten Beispiel (siehe Referenz).
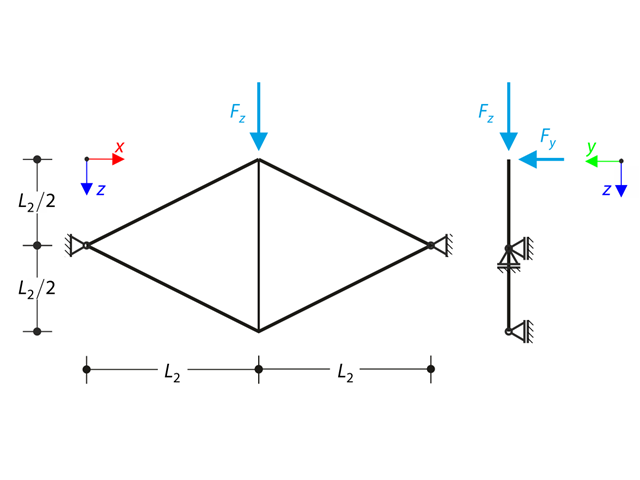
Der ebene Fachwerkträger aus vier geneigten Stäben und einem vertikalen Stab wird am oberen Knoten mit der Vertikalkraft Fz und einer außerhalb der Ebene liegenden Kraft Fy belastet. Bei Theorie III. Ordnung und unter Vernachlässigung des Eigengewichts sind die Normalkräfte der Stäbe und die Verschiebung des oberen Knotens uy aus der Ebene zu bestimmen. Das Verifikationsbeispiel basiert auf dem Beispiel von Gensichen und Lumpe.
Im aktuellen Validierungsbeispiel wird der Winddruckwert sowohl für die allgemeine Tragwerksplanung (Cp,10 ) als auch für örtliche Tragwerksnachweise, wie z. B. Verkleidungs- oder Fassadensysteme (Cp,1 ) basierend auf dem Flachdachbeispiel [1] and Japanische Windkanal-Datenbank . Die empfohlene Einstellung für ein dreidimensionales Flachdach mit spitz zulaufender Traufe wird im nächsten Teil beschrieben.
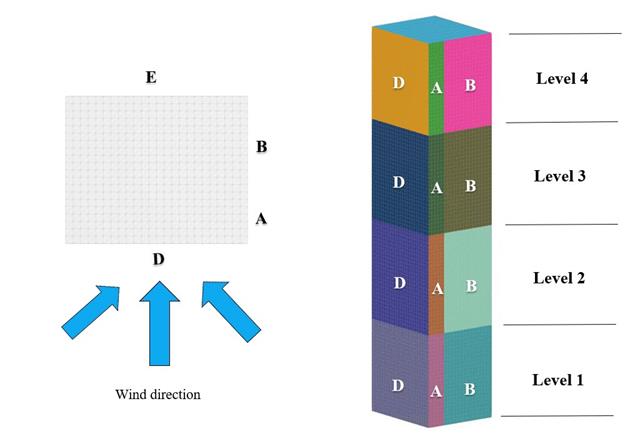
Im aktuellen Validierungsbeispiel untersuchen wir den Winddruckbeiwert (Cp) von Flachdächern und -wänden mit ASCE7-22 [1]. In den Abschnitten 28.3 (Windlasten - Hauptwindkraftaufnahmesystem) und Bild 28.3-1 (Lastfall 1) ist der Cp-Wert für verschiedene Dachneigungen tabellarisch dargestellt.
Das Modell basiert auf dem Beispiel 4 aus [1]: Punktgestützte Platte.
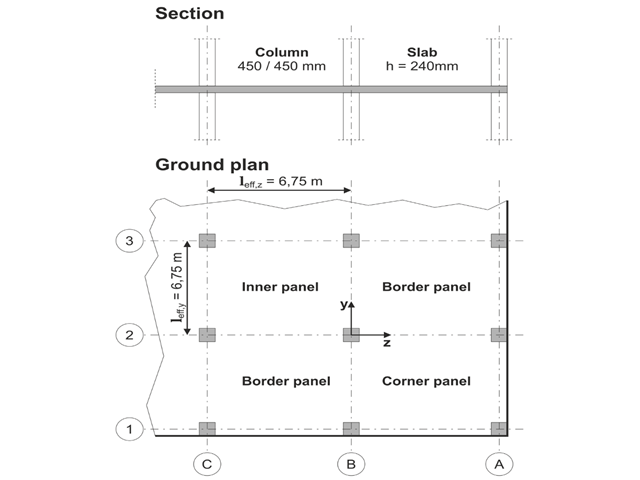
Die Flachdecke eines Bürogebäudes mit rissempfindlichen Leichtbauwänden soll bemessen werden. Es sind Innen-, Rand- und Eckfelder zu untersuchen. Die Stützen und die Flachdecke werden monolithisch gefügt. Rand- und Eckstützen werden bündig mit dem Deckenrand platziert. Die Achsen der Stützen bilden ein quadratisches Raster. Es handelt sich um ein biegesteifes System (Gebäude mit Schubwänden ausgesteift).
Das Bürogebäude hat 5 Stockwerke mit einer Stockwerkshöhe von 3,000 m. Die anzunehmenden Umgebungsbedingungen werden als "geschlossene Innenräume" definiert. Es gibt überwiegend statisch wirkende Einwirkungen.
Der Fokus in diesem Beispiel liegt auf der Ermittlung der Plattenmomente und der erforderlichen Bewehrung über den Stützen unter Volllast.
Das Modell basiert auf dem Beispiel 4 von [1]: Punktgestützte Platte. Die Schnittgrößen und die erforderliche Längsbewehrung sind dem Nachweisbeispiel 1022 zu entnehmen. In diesem Beispiel wird das Durchstanzen in der Achse B/2 untersucht.
Das Architectural Institute of Japan (AIJ) hat eine Reihe an bekannten Benchmark-Szenarien für Windsimulation vorgestellt.
Der Nachfolgende Beitrag dreht sich dabei um den "Case E - a building complex in an actual urban area with dense concentration of low-rise buildings in Niigata City".
Im Folgenden wird das beschriebene Szenario in RWIND2 nachgebildet und die Ergebnisse mit den simulierten und der experimentellen Resultate des AIJ verglichen.
Im aktuellen Validierungsbeispiel untersuchen wir den Winddruckwert sowohl für allgemeine statische Nachweise (Cp,10 ) als auch für Bekleidungs- bzw. Fassadenbemessung (Cp,1 ) von Gebäuden mit rechteckigem Grundriss mit EN 1991-1-4 [1]]]. Es gibt dreidimensionale Fälle, auf die wir im nächsten Teil näher eingehen werden.
Das Architectural Institute of Japan (AIJ) hat eine Reihe an bekannten Benchmark-Szenarien für Windsimulation vorgestellt.
Der Nache Beitrag dreht sich dabei um den "Fall A - Hochhaus mit 2:1:1 Form".
Im Folgenden wird das beschriebene Szenario in RWIND2 nachgebildet und die Ergebnisse mit den simulierten und experimentellen Ergebnissen des AIJvergleich.
Das Architectural Institute of Japan (AIJ) hat eine Reihe an bekannten Benchmark-Szenarien für Windsimulation vorgestellt.
Der Nachfolgende Beitrag dreht sich dabei um den "Case D - high-rise building among city blocks".
Im Folgenden wird das beschriebene Szenario in RWIND2 nachgebildet und die Ergebnisse mit den simulierten und der experimentellen Resultate des AIJ verglichen.
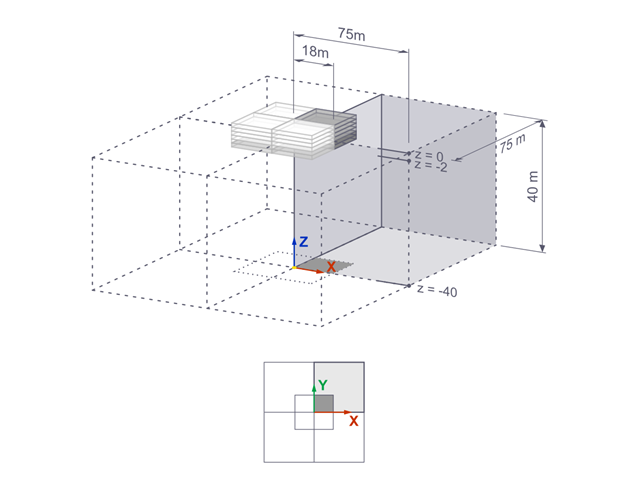
Die Setzungen eines starren quadratischen Fundaments gegründet auf Seeton [1] werden mit RFEM berechnet. Ein Viertel des Fundaments wird modelliert. Das Fundament hat an beiden Seiten eine Breite von 75,0 m. Zur Generierung der Ergebnisse werden Bauzustände verwendet.
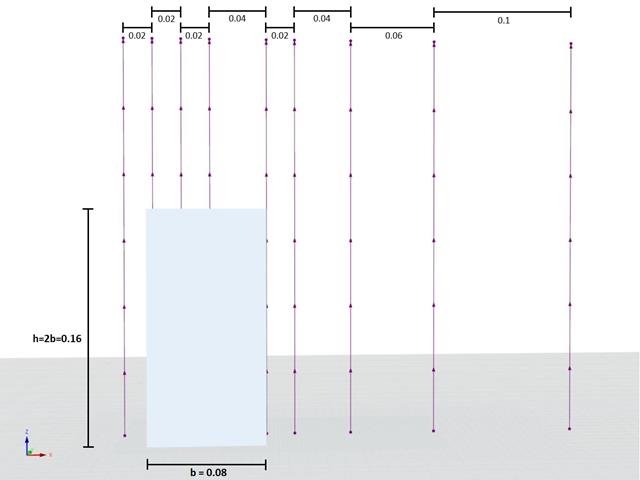
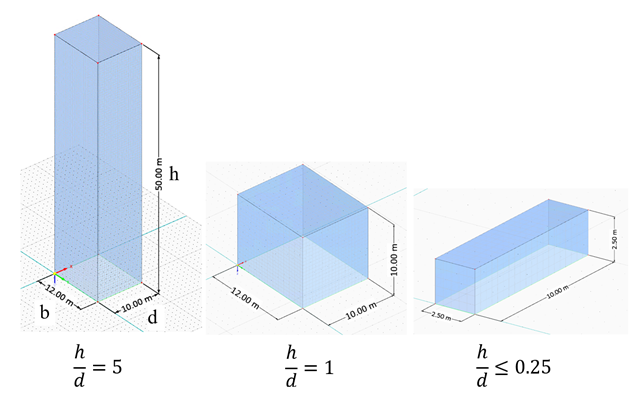
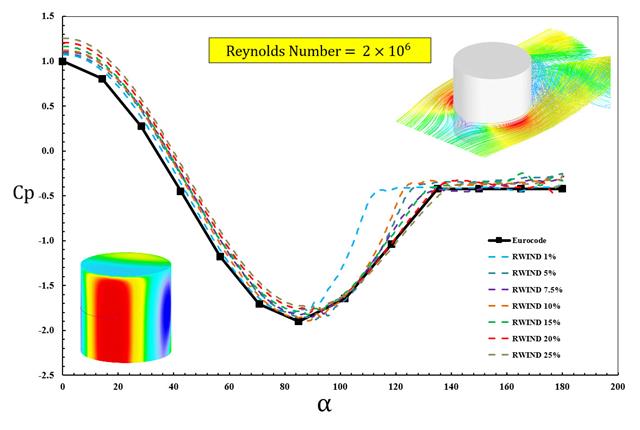
Im aktuellen Validierungsbeispiel untersuchen wir den Windkraftbeiwert (Cf ) von Würfelformen mit EN 1991-1-4 [1]. Es gibt dreidimensionale Fälle, auf die wir im nächsten Teil näher eingehen werden.
In den verfügbaren Normen wie EN 1991-1-4 [1], ASCE/SEI 7-16 und NBC 2015 sind Windlastparameter wie der Winddruckbeiwert (Cp) für Grundformen aufgeführt. Wichtig dabei ist, wie Windlastparameter schneller und genauer berechnet werden können, anstatt mit zeitraubenden und teilweise komplizierten Formeln in Normen zu arbeiten.
Es sollen mittels LRFD und ASD die erforderlichen Festigkeiten und Knicklängenbeiwerte der Stützen gemäß ASTM A992 eines biegesteifen Rahmens (Bild 1) bestimmt werden, wobei die maximale Auflastkombination zu berücksichtigen ist.