Bei der CFD-Simulation (Computational Fluid Dynamics) handelt es sich um ein wertvolles Werkzeug für verschiedene Bereiche des Ingenieurwesens, des Designs und der Forschung. Wir stellen Ihnen nachfolgend einige der bedeutendsten Vorteile von CFD-Simulationen genauer vor.
Kosteneffizienz
Der Einsatz von CFD-Simulationen in großen oder komplexen Systemen gestaltet sich wesentlich kostengünstiger als die Durchführung physikalischer Experimente. Durch die digitale Windsimulation entfallen beispielsweise Kosten für die Herstellung von Prototypen, die Sicherung von Testeinrichtungen und die Verwendung von Spezialgeräten.
Zeitersparnis bei CFD-Simulationen
Auch im Analyseprozess können Sie mit einer CFD-Simulation einiges an Zeit einsparen. Die schnelle Einrichtung und Ausführung ist mit wenigen Klicks erledigt und somit wesentlich zeitsparender als der Aufbau eines physikalischen Tests. Dadurch profitieren Sie als Ingenieur von iterativeren Analyseprozessen. Testen Sie Ihre Entwürfe in einer virtuellen Umgebung und perfektionieren Sie alle Aspekte digital, bevor Sie sich letztendlich für einen passenden physischen Prototypen entscheiden.
Detaillierte Visualisierung
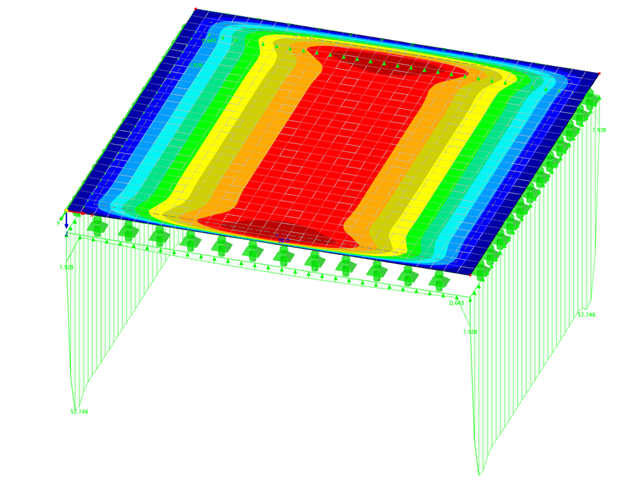
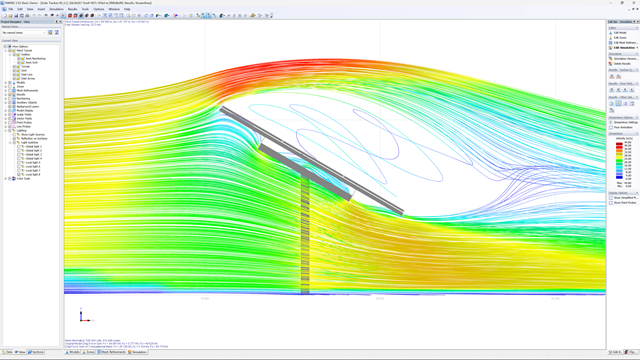
Sie erhalten durch CFD beispielsweise Strömungsmuster, Druckverteilungen und andere relevante physikalische Phänomene, die Sie experimentell nur schwer oder gar nicht nachweisen könnten. Durch diese weiteren Informationen erhalten Sie eine noch bessere Einsicht in die technischen Daten Ihres Projekts.
Skalierbarkeit bei CFD-Simulationen
Ein weiterer Vorteil von CFD-Simulationen ist die beliebige Skalierbarkeit ohne großen Aufwand. Sie wollen verschiedene Größen oder Konfigurationen einer Analyse untersuchen? Im digitalen Strömungskanal ist dies ohne physische Änderungen oder neue Prototypen problemlos möglich. Durch eine CFD-Simulation steht Ihnen eine breitere Palette von Szenarien und Analyseparametern zur Verfügung.
Nachhaltigkeit durch CFD-Simulationen
Indem Sie durch CFD-Simulation weniger physische Prototypen bauen und Experimente durchführen müssen, zeigt sich ein weiterer der Vorteile einer CFD-Simulation. Ein geringerer Energieverbrauch und eine geringere Abfallproduktion eignen sich hervorragend zur Umsetzung von Nachhaltigkeitszielen wie verringerten Materialkosten und Umweltaspekten.
Komplexität und Präzision
Durch einen digitalen Windkanal eröffnet sich Ihnen die Möglichkeit, komplexe Geometrien und Fluidwechselwirkungen genau zu modellieren. In einem Versuchsaufbau wäre dies nur schwer zu replizieren. Die Präzision von CFD ermöglicht Ihnen die Analyse subtiler Effekte und Wechselwirkungen in einer kontrollierten Umgebung. Gleichzeitig liefert Ihnen das Programm komplexe Einblicke, die das Verständnis und die Optimierung von Systemen verbessern.
CFD-Simulationen sind dann besonders nützlich, wenn Sie über ein umfassendes Verständnis der zugrunde liegenden Modelle und Annahmen verfügen. In den meisten Fällen arbeiten Sie für ein allumfassendes Ergebnis am besten mit einer Kombination aus CFD-Simulationen und experimentellen Tests. Auf diese Weise bietet sich Ihnen die Möglichkeit, das Verhalten Ihrer Strukturen in Strömungssituationen vollumfänglich zu erfassen.
Sie suchen nach einer Möglichkeit, CFD-Simulationen für Ihre Projekte durchzuführen? Das leistungsfähige RWIND ist ein eigenständig lauffähiges Programm, das Ihnen Strömungssimulationen in verschiedensten Situationen ermöglicht. Hier finden Sie weitere Informationen zur neuesten Software-Generation:
RWIND 2
.
Mehr anzeigen