The topic can be illustrated easily on a single-span beam. For this, three structural systems are described below. These models are documented in the attached file.
System 1
Statically determined system (no foundation), dT = 80° on the top side
The member is curved upwards, but is free of stress in itself.
System 2a
Like System 1, but with an additional member elastic foundation. The member elastic foundation is entered without a possible failure (nonlinearity).
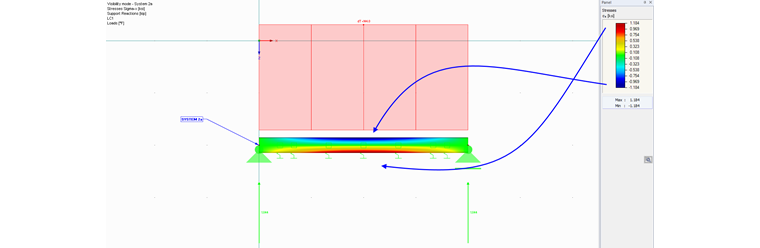
If you display the stresses sigma_x of the member for System 2a, you obtain compression on the top side of the member and tension on the bottom side of the member (see Image 01).
Due to the curvature of the member and the existing member elastic foundation, a contact force p‑z occurs to impede the upward curvature of the member (see Image 02).
These contact forces p‑z (Image 02) are caused by the curvature of the member due to the temperature and applied member elastic foundation. The illustrated contact forces can be replaced by a member load opposite the curvature. This is shown in System 2b in the example file.
System 2b
The member elastic foundation is removed and a variable member load is entered in the Z-direction.
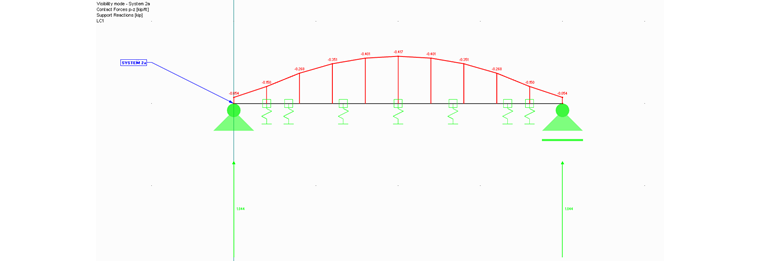
When comparing the results (for example, the deformations u‑z) on both systems 2a and 2b, you obtain the equivalent results (see Image 03).
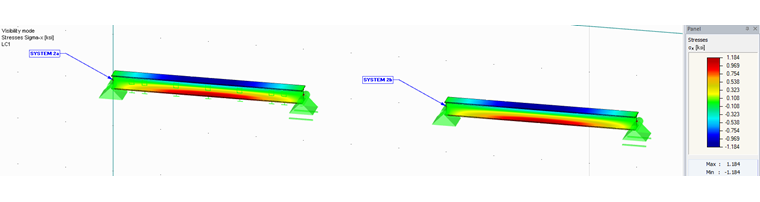
Moreover, you can also display the stresses sigma_x for both System 2a and System 2b. These also have the same value (see Image 04).
System 3 should only document the stresses due to the temperature difference on a statically determined system (without foundation).
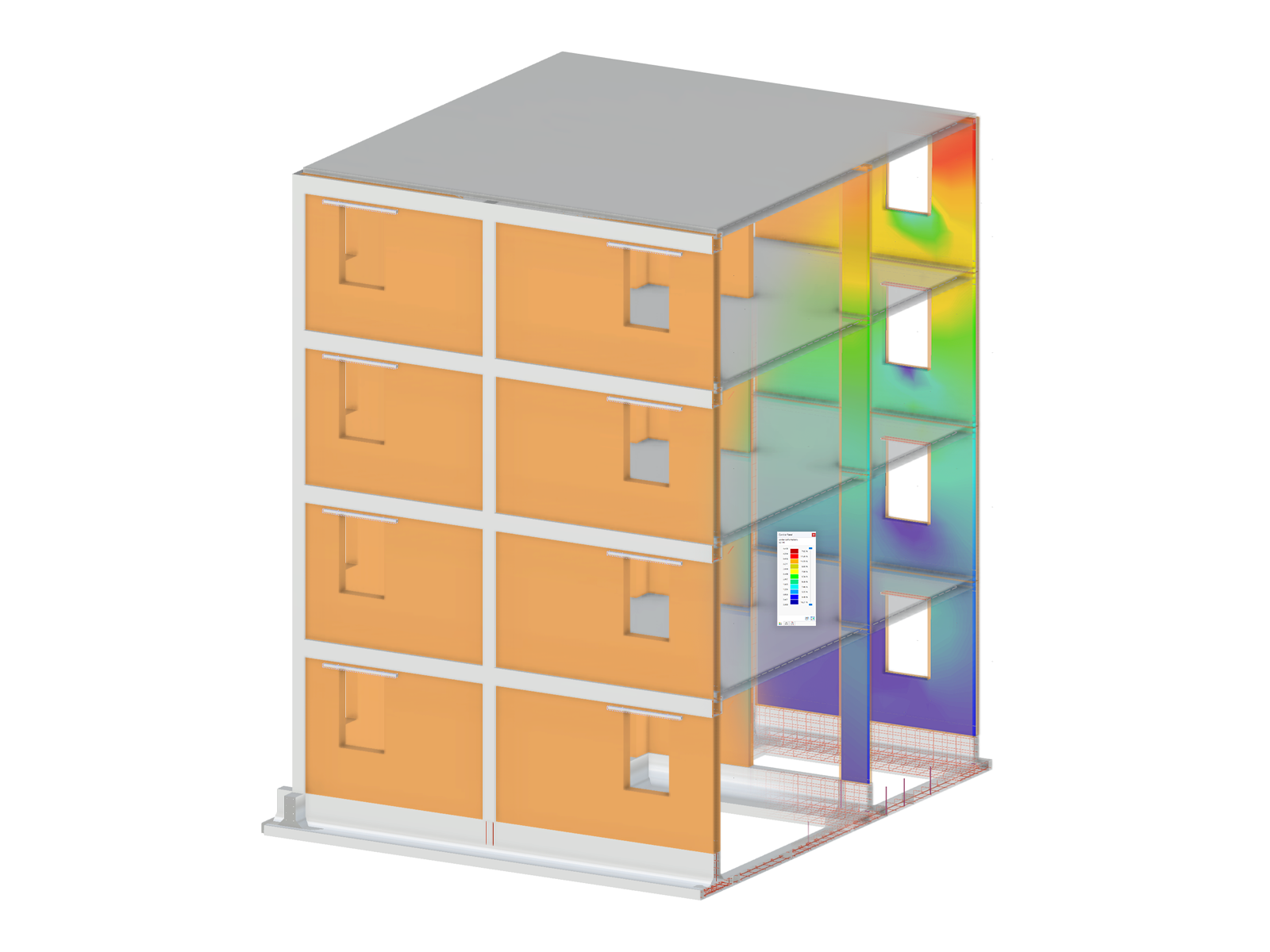
The results documented in the "single-span beam" example can also be transferred to surfaces with elastic foundations.















































.png?mw=600&hash=49b6a289915d28aa461360f7308b092631b1446e)