3144x

2017-01-04

Modeling of Point-Supported Glass Systems 1

Durch die Transparenz des Werkstoffes Glas darf dieser in keinem Bauwerk fehlen. Neben den typischen Einsatzfeldern von zum Beispiel Fenstern wird der Baustoff zunehmend auch in den Gewerken der Fassade, bei Vordächern oder auch als Ausfachung bei Treppen verwendet. Dabei wird natürlich von den planenden Architekten oftmals ein sehr hohes Maß an Transparenz an die Befestigung der Glasscheiben gestellt. Hierzu werden die sogenannten Punkthalter für Glasscheiben benötigt.

Design Background

In addition to the general technical approvals of the individual producers, the design of point-supported fittings is regulated in DIN 18008 [1]. This German standard specifies two different ways:

Annex B - Verification/Validation of finite element models
Annex C - Simplified method

In addition to the various design options, there are constructional provisions - especially for plate fittings - specifying the geometrical arrangement on a glass pane or the formation in the edge area.

Initial Data Used for Analysis

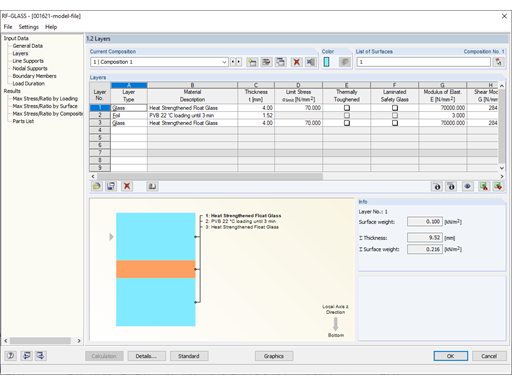
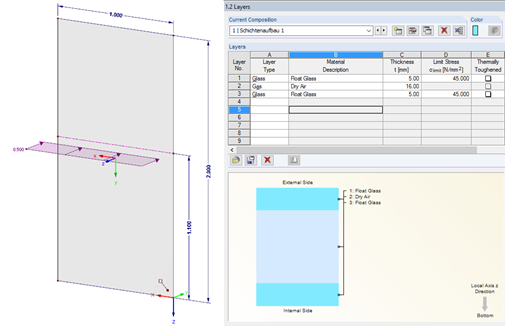
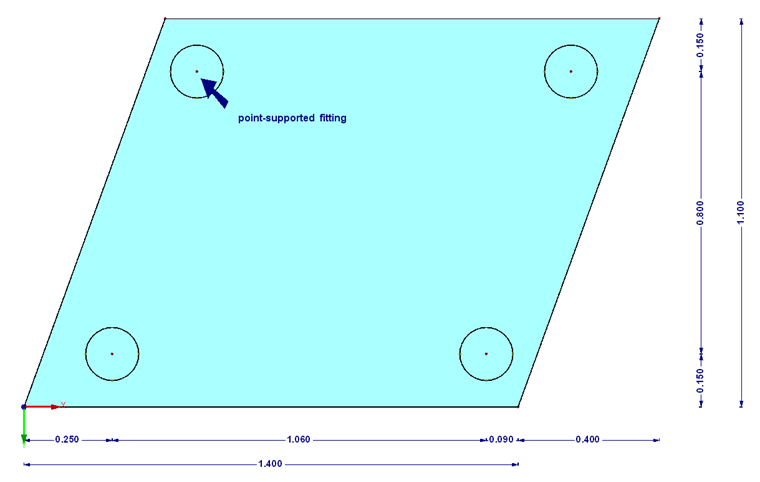
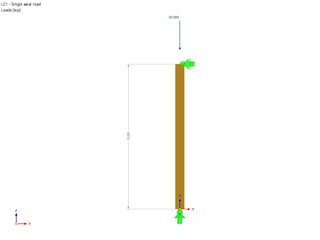
Laminated safety glass from heat-strengthened float glass 2 x 8 mm
Point fixing PH 793 by Glassline GmbH (approval Z-70.2-99 [3]), cylindrical head Ø 52 mm, drilling Ø 25 mm
Design load q_d = 4.5 kN/m²

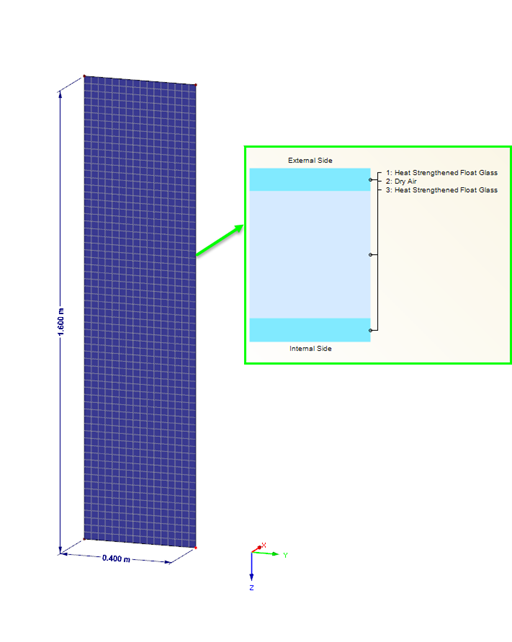
System with Dimensions

Modeling in RFEM According to Simplified Method

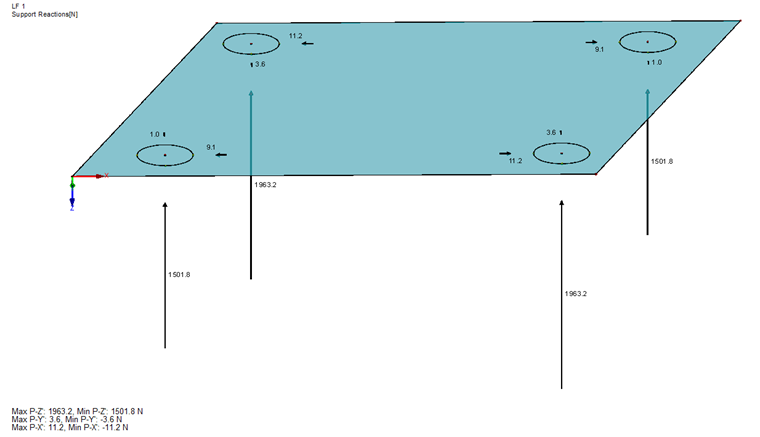
In the case of glass pane design according to the simplified method described in DIN 18008, Annex C [1], the pane may be analyzed without the drilling holes. The existing glass fittings are represented by springs. The existing spring stiffness is specified in the technical approval. In our example, it gives the following result:

C_Z,max = 1/24,372 + 1/3,015 = 2,683 N/mm
C_Z,min = 1/15,386 + 1/1,592 = 1,443 N/mm
C_Z,sel = 2,000 N/mm
C_V;x,y = 344 N/mm

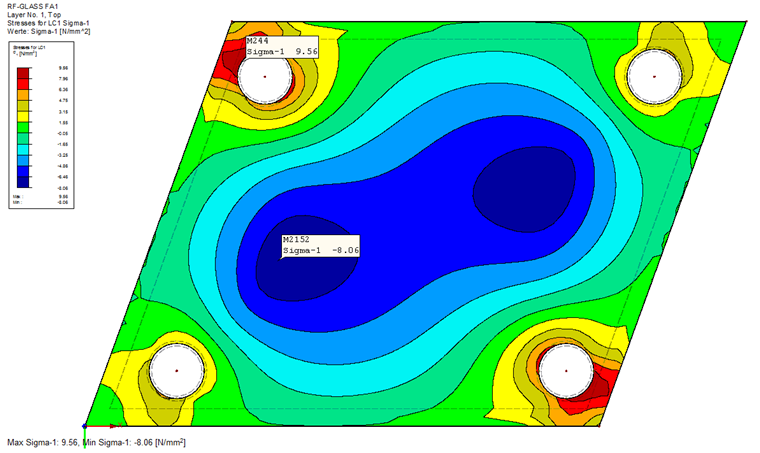
The following result values are calculated on the basis of the mentioned parameters.

Support Reactions - Local Results

Stresses - Local Results

All relevant stress ratios can now be calculated using the formulas and parameters provided by DIN 18008, Annex C [1].

Stress component F_Z:

σ_{Fz} = \frac{b_{Fz}}{d ²} \cdot \frac{t_{ref}^{2}}{t_{i}^{2}} \cdot F_{Z} \cdot δ_{Z} = \frac{15, 8}{25 ²} \cdot \frac{102}{82} \cdot 1.964 \cdot 0, 5 = 38, 8 N / mm ²

Formula 1

Stress component F_res:

\begin{array}{l} F_{res} = \sqrt{F_{x}^{2} F_{y}^{2}} = \sqrt{11 ² 4 ²} = 12 N \\ σ_{F, res} = \frac{b_{F, res}}{d ²} \cdot \frac{t_{ref}}{t_{i}} \cdot F_{res} \cdot δ_{F, res} = \frac{3, 92}{25 ²} \cdot \frac{10}{8} \cdot 12 \cdot 0, 5 = 0, 1 N / mm ² \end{array}

Formula 2

Stress component M_res:
Due to the hinged support around axes x, y, and z, there is no additional moment M_res.

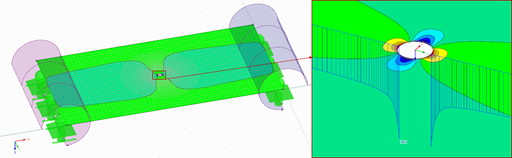
Stress concentration in the drilling hole area:
σ_g = σ_g(3d) ∙ δ_g ∙ k = 9.6 ∙ 8 / 10.8 ∙ 1.6 = 11.4 N/mm²

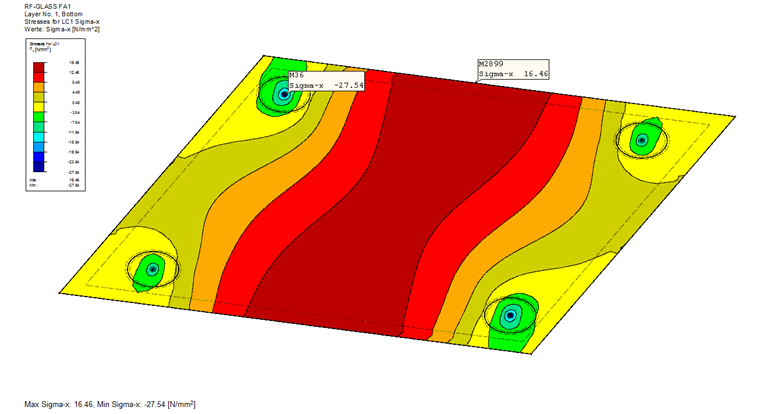
The governing design stress value in the fitting area then results from the sum of the individual components.
E_d = 38.8 + 0.1 + 11.4 = 50.3 N/mm²

As the final step, the moment in the span must be considered. In this case, the moment has to be determined on a statically defined system.

Stress Analysis in Span Area

The governing stress in the span area is E_d = 16.5 N/mm².

The allowable stress for laminated safety glass is calculated as

R_{d} = 1.1 \cdot \frac{f_{k, TVG}}{γ_{M}} = 1.1 \cdot \frac{70}{1.5} = 51.3 N / mm ²

Formula 3

and thus gives the result of the total design ratio of the glass η = 0.98.

In addition to the general stress analysis performed here, you can perform additional designs for the exact dimensions of the glass pane. For this, you can follow the standard.

Summary

Annex C of the German standard DIN 18008 provides very simple tools for designing point-supported glass fittings. By using the table values, you can very quickly estimate the structural behavior of the glass pane and determine the design ratio. Another option is specified in Annex B of the standard. This design method based on a finite element model will be explained in the next part of this article.

Literature

[1]	DIN 18008-3:2013-07
[2]	Weller, B.; Engelmann, M.; Nicklisch, F.; Weimar, T.: Glasbau-Praxis: Konstruktion und Bemessung Band 2: Beispiele nach DIN 18008, 3rd ed.). Berlin, Beuth.
[3]	General Technical Approval Z-70.2-99, dated 4th of September, 2014

Author

Mr. Lex is responsible for developing products for glass structures and for quality assurance of the RFEM program. He also provides technical support for our customers.

Links

Structural Analysis and Design Software for Glass Structures

Downloads

RFEM Model File

8.12 MB

Do you have any questions?

Events

2024-04-24

Online Training

RFEM 6 | Students | Introduction to FEM

2024-04-25

Stiffening Design in RFEM 6 Using Building Model

Webinar

Stiffening Design in RFEM 6 Using Building Model

2024-04-25

AISC 360-22 Steel Connection Design in RFEM 6

Webinar

AISC 360-22 Steel Connection Design in RFEM 6 (USA)

2024-04-30

Online Training

RFEM 6 | Students | Introduction to Timber Design

2024-05-02

Construction Stages in Membrane Structures with RFEM 6

Webinar

Construction Stages in Membrane Structures with RFEM 6

2024-05-08

Online Training

RFEM 6 | Students | Introduction to Reinforced Concrete Design

2024-05-09

$Cross-Section Modeling and \n Stress Analysis in RSECTION 1$

Webinar

Cross-Section Modeling and Stress Analysis in RSECTION 1

2024-05-15

Online Training

RFEM 6 | Students | Introduction to Steel Design

2024-05-16

Consideration of Construction Stages in RFEM 6

Webinar

Consideration of Construction Stages in RFEM 6

2024-05-23

Most Frequently Asked Questions Answered by Dlubal Support Team

Webinar

Most Frequently Asked Questions Answered by Dlubal Support Team | May 2024

2024-05-29

$Steel Structures in RFEM 6 \n Part 1: Modeling, Load Input$

Webinar

Modeling and Design of Steel Structures in RFEM 6 | Part 1: Modeling, Load Input

2024-06-06

$Steel Structures in RFEM 6 \n Part 2: Combinations, Design, Documentation$

Webinar

Modeling and Design of Steel Structures in RFEM 6 | Part 2: Combinations, Design, Documentation

Videos

Knowledge Base

KB 001621 | Calculation and Use of Laminated Glass

Length: 00:00:31 min

Event

Webinar | Construction Stage Analysis in RFEM 6

Length: 00:48:53 min

Event

Glass Design with Dlubal Software

Length: 00:00:00 min

Event

Glass Design with Dlubal Software

Length: 00:36:44 min

Knowledge Base

KB 000949 | FE Mesh Settings

Length: 00:00:50 min

Knowledge Base

KB 000850 | Saving User-Defined Layer Structures

Length: 00:00:30 min

Knowledge Base

KB 000871 | Force Load Distribution of Individual Load Cases on Different Insulating Glass Layers

Length: 00:00:33 min

Knowledge Base

KB 000783 | Calculation Option 2D/3D for Laminated Glass

Length: 00:00:21 min

Knowledge Base

KB 000759 | 3D Rendering for Display of Support Definitions

Length: 00:00:24 min

Playlist

Models to Download

813x

60x

Curved Vertical Glazing

1110x

47x

Suspension Bridge

1252x

92x

Structural Facade

215x

FTS004 | Roof Planes with Different Inclination, Centrally Supported

191x

FTS003 | Horizontal Roof Planes with Central Supports

3D Model of Facade Structure in RSTAB (© Huana Engineering Consulting (Beijing) Co., Ltd. (SuP Ingenieure GmbH))

712x

Steel Facade Structure

3D Model of Steel-Glass Façade in RSTAB (© SuP Ingenieure GmbH)

485x

Steel and Glass Facade

424x

Verification Example 0024 | 3

546x

Verification Example 0024 | 5

Knowledge Base Articles

Different glass types and layer structures are available for glass structures used for different purposes. The following types are usually used: float glass, partly tempered glass, and toughened safety glass.

The proportion of glass used when planning a building is increasing. Open, light-flooded buildings represent the modern art of architecture. However, specialized engineers have to face new challenges during planning. One such example is ceiling-high glass facades loaded by a handrail. The influence of this loading, as well as the calculation of the deformation, are shown in this article.

Loading panes of insulating glass due to climatic effects are clearly regulated in DIN 18008. In the case of the corresponding pane geometry, this load type can also govern for the ultimate limit state design. The FE design on the entire structure with the space between panes represented as the volume of a gas provides exact results for the analysis. However, a plausibility check is also becoming increasingly important. This article shows various options for performing these checks.

As mentioned in Part 1, according to the current standard DIN 18008-3, it is allowed in glass construction to represent point supports for glass components by means of FEM in order to design the adequate ultimate limit state. The rules are described in Annex B of the standard [1].

Product Features

The global calculation assigns the stiffness determined by means of the selected composition and the glass geometry to each surface. Then, the calculation proceeds using the plate theory. It is possible to select whether the shear coupling of layers should be considered.

In the case of the local calculation, you can further specify 2D or 3D calculation. Two-dimensional calculation means that the single-layer or laminated glass is modeled as a surface, whose thickness is calculated on the basis of the selected structure and glass geometry (using the plate theory). Similarly to the global calculation, you can optionally consider shear coupling of layers.

The 3D calculation uses solids in the model to substitute each composition layer. This way, the results are more accurate, but the calculation may take more time.

It is possible to model insulating glass only if local calculation is selected. The gas layer is always modeled as a solid element, so it is necessary to design individual insulating glass parts independently of the surrounding structure. The ideal gas law (thermal equation of state of ideal gases) is considered for the calculation and the third-order analysis.

In the add-on module, select the surfaces to be designed (for example, by using the Select function). The geometry of the glass pane, as well as the loads, is imported from the RFEM model.

Then, you have to decide if the calculation should be performed without the influence of the surrounding structure (local calculation) or with consideration of this influence (global calculation). If you select the local calculation, each surface selected for the design is detached from the model and calculated separately.

The global calculation considers the entire structure, including entered glass panes. All glass composition data and glass properties of individual layers are to be defined in RF-GLASS input windows. You can select layers of type glass, foil, and gas. The desired material can be imported directly from the library, which contains a large number of materials.

All parameters of individual layers, including their thicknesses, are editable. In addition, you can create a number of compositions in RF-GLASS, allowing you to design different types of glass together.

For insulating glass, you can consider external loads as well as loads due to temperature, atmospheric pressure, and altitude changes for the analysis. The module calculates these loads automatically on the basis of climatic load parameters. If you select the local calculation type, it is necessary to define line supports, nodal supports, and boundary members of the surfaces in RF-GLASS. These supports and members are considered in RF-GLASS only and have no influence on the model created in RFEM.

After the calculation, the results are displayed in clearly arranged result windows. Thus, you can easily find the maximum stress ratio. The stress diagram by composition is displayed as well.

Furthermore, RF-GLASS displays a parts list and, for insulating glass, the gas pressure. It is possible to display the results graphically in the RFEM model.

Both input and result tables of RF-GLASS, including graphics, can be added to the RFEM printout report. In addition, it is possible to export all tables to MS Excel.

RF-GLASS Add-on Module for RFEM | Analysis and Design of Glass Surfaces

Design of single-layer or laminated glass as well as gas layer insulating glass
design of curved glass
Option to select either local calculation without regard to the influence of a surrounding structure, or global calculation with regard to the influence of an entire structure
Calculation of limit stresses according to DIN 18008:2010-12 or TRLV:2006-08
Assignment of loads to load duration classes
Extensive material library including all common glass, foil, and gas types in compliance with the DIN 18008:2010-12, E DIN EN 13474 standards, and the TRLV:2006-08 regulation
Optional consideration of shear coupling of layers
Consideration of climatic loads
Calculation according to the linear static analysis or nonlinear analysis according to the large deformation analysis. analysis
Stress analysis, ultimate limit state design, serviceability limit state design
Graphical representation of all results in RFEM
Possibility to filter results and color scales in result tables
Direct data export to MS Excel