20377x

2017-02-01

Actions on Silos According to EN 1991-4

Silos are used as large containers for storage of bulk materials such as agricultural products or source materials as well as intermediates of industrial production. The structural engineering of such structures requires a precise knowledge of the stresses due to particulate solids in the building structure. The standard EN 1991‑4 "Actions on Silos and Tanks" [1] provides the general principles and requirements for determining these actions.

Application Area

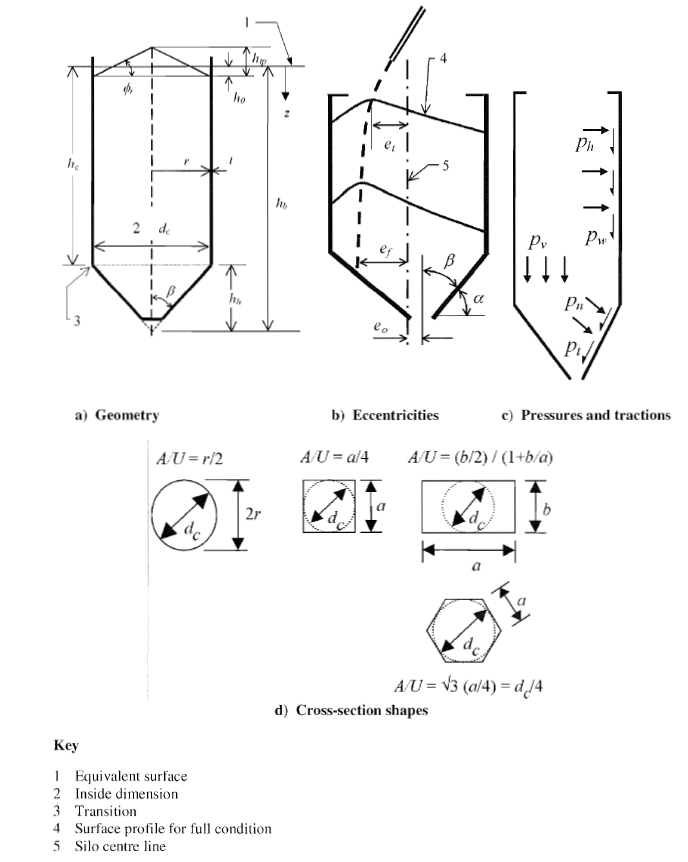
The application of the design rules for silos and tanks is subjected to geometrical limitations. In [1], the geometric dimensions are limited to h_b / d_c < 10 with h_b < 100 m and d_c < 60 m. In addition, the application limits depend on the cross-section shape of the silo and on the stored solids.

Display of Silo Cells with Names of Geometric Parameters and Loads, Source: DIN EN 1991-4

Properties of Particulate Solids

Annex E of [1] specifies the parameters of the most common solids stored in silos, showing the range of particulate solid properties. Furthermore, Section 4 and Annex C of [1] describe the test methods for determining the properties of the stored solids.

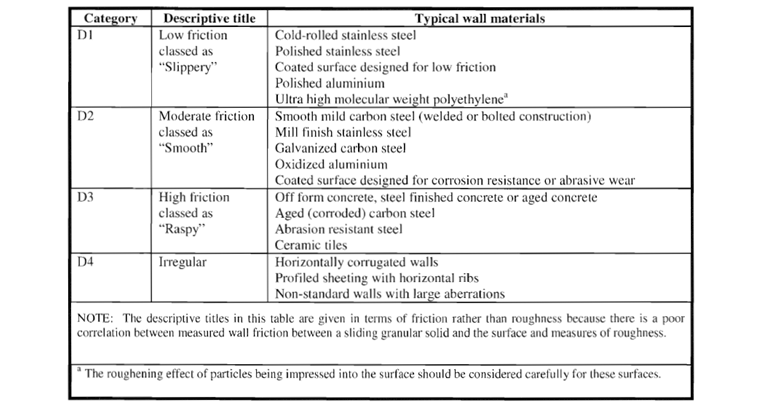
Wall frictional properties of the particulate solids take into account the roughness of wall surfaces where the solids slide along. Table 4.1 of [1] describes the various categories of wall surfaces. The categories of the wall surfaces are shown in the table below. Annex D.2 of [1] also provides information for the evaluation of the wall friction coefficient for the D4 category.

Wall Surface Categories, Source: DIN EN 1991-4

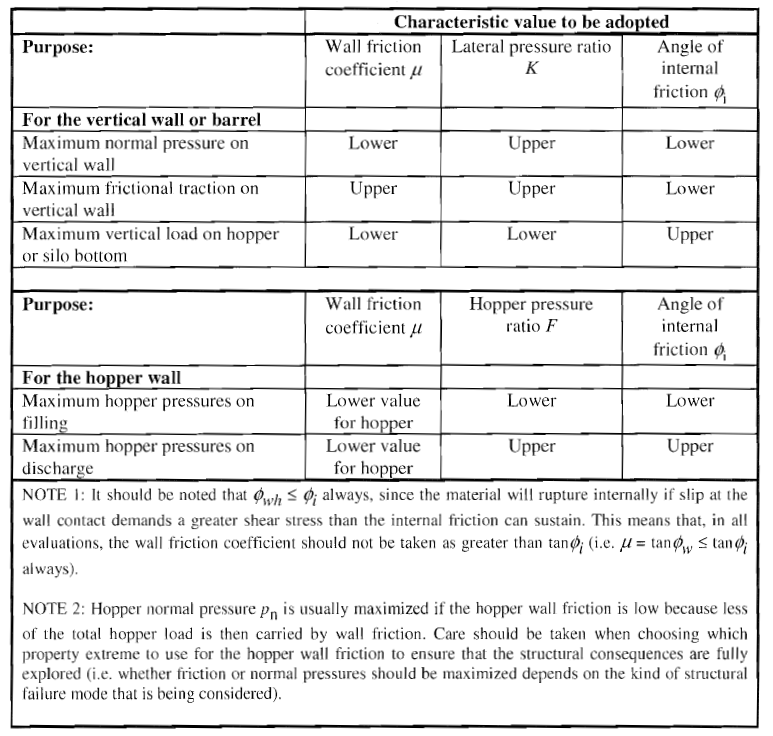
You should always determine the loads of a load case for a particular combination of the relevant solid properties. For each of these load cases, the extreme values are reached when the solid properties take different extreme values within the discharge flow of the particulate solids. The extreme values of the bulk material parameters to be used for each of the load cases to be analyzed are given in Table 3.1 of [1]. The relevant parameters for various load applications are included in the following table.

Relevant Parameters for Different Load Applications, Source: DIN EN 1991-4

Structural Class

Silo cells are divided into three action assessment classes according to their storage capacity and eccentricity in compliance with Table 2.1 of [1].

Classification of Design Situations, Source: DIN EN 1991-4

Various differentiated or simplified loading assessments are adopted according to the respective action assessment class.

Loads on Vertical Walls of Silos

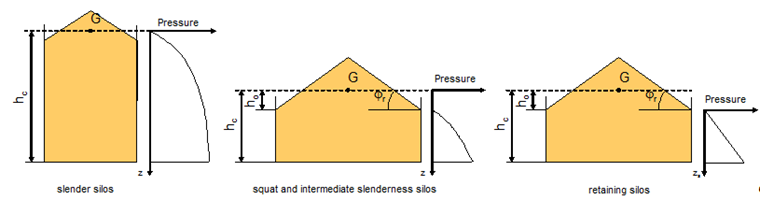
Loads on the vertical walls of silos are subjected to a differentiated calculation considering the silo slenderness. A distinction is made between:

slender silos (h_c / d_c ≥ 2.0),
silos with medium slenderness (1.0 < h_c / d_c < 2.0),
low silos (0.4 < h_c / d_c ≤ 1.0), and
retaining wall silos (h_c / d_c ≤ 0.4 and horizontal silo floor)

Silo Pressure Distribution Depending on Slenderness of Silo

Symmetrical Loads
Symmetrical loads are fixed loads that are uniformly distributed over the silo circumference. Discharge loads arise when the uniform loads in full condition are increased by a load-magnifying factor.

Asymmetrical Loads
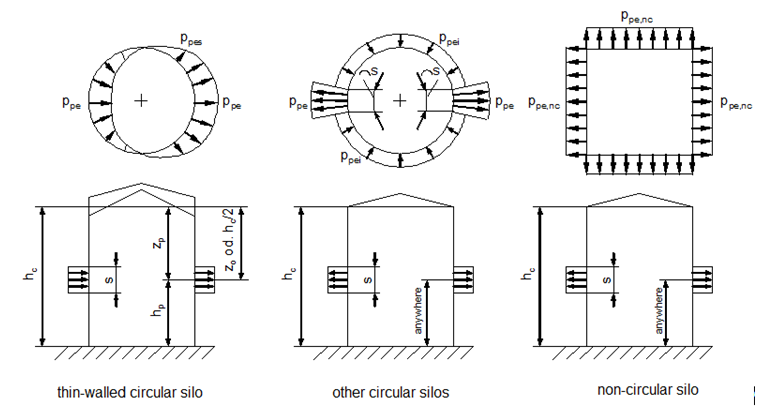
Besides the fixed loads, additional free loads are usually to be applied. Distributions of unsymmetrical loads (patch loads) in a silo are caused by actions due to imperfections or eccentricities during filling and discharge of solids.
For thick-walled circular silos, the patch load shall be applied to a square area with the side length s on opposite sides. In the case of non-circular silos, the patch loads can be taken into account by increasing the symmetrical loads. The outward patch pressure should be taken to act on a horizontal band on the silo wall at any level, over a vertical height s.

Application of Partial Surface Loads, Source: DIN EN 1991-4

Generally, it is unnecessary to apply the patch loads in the case of squat and intermediate slenderness silos.
For silos in Action Assessment Class 2, the patch load method may be approximately used by uniformly increasing horizontal pressures.

Discharge Loads with Large Eccentricities
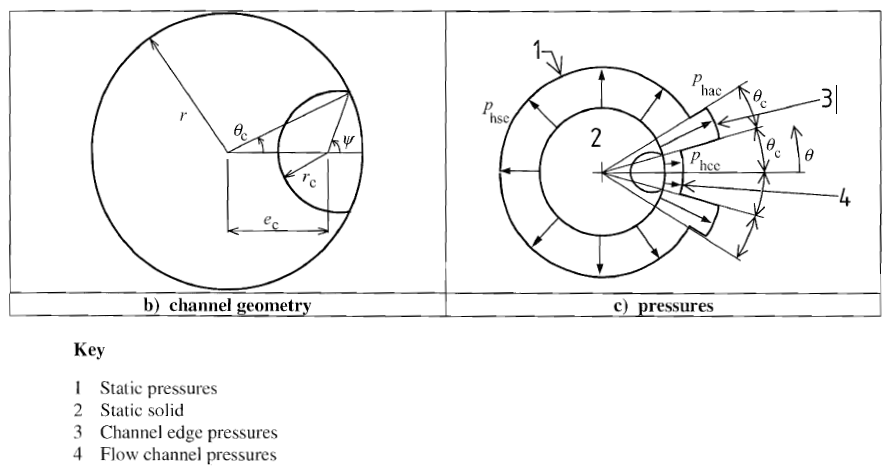
According to [1], loads due to large discharge eccentricities should be used as a separate load case. The development of this loading assessment is based on the premise that a flow channel may occur near the wall as a result of large eccentric discharge. A circular flow channel is assumed, which is constant due to the height of the silo wall, and intersects the silo wall at an opening angle θ_c.

Flow Channel and Pressure Distribution for Silos with Large Discharge Eccentricities, Source: DIN EN 1991-4

However, a theoretical prediction of the geometric shape of a discharge hopper is hardly possible with the tools currently available. Therefore, the flow channel must be specified. The calculation is performed with at least three different flow channel radii rc in order to determine the apparent variations of the flow channel.

Lower horizontal pressures occur outside the flow channel in the contact areas of the flowing solid and the silo wall. The loads of the filling load case apply in the latter area. The pressure is increased directly next to the flow channel up to the opening angle of 2 θ_c.

Large Eccentricity Filling Loads
Loads due to eccentric filling must be considered for squat or intermediate slenderness silos.

EN 1991‑4 [1] explains the determination of the additional vertical force (compressive) in the wall per unit length of circumference at any depth z_s below the point of highest wall contact. This force per unit circumference should be added to the force arising from wall friction.

Filling Pressures for Eccentrically Filled Low or Medium-Slender Silos, Source: DIN EN 1991-4

Loads on Silo Hoppers and Silo Bottoms

The loads on the walls of silo hoppers should be determined with regard to the steepness of the hopper walls according to [1].

Filling and Discharge Pressures in One Hopper, Source: DIN EN 1991-4

The standard distinguishes between flat bottoms as well as steep and shallow hoppers. In the case of steep hoppers, there is an additional distinction between the load cases of filling and discharge. Kick load at the transition from the vertical walled section to the hopper is already included in the load distributions.

Annex G of [1] provides alternative rules for pressures in hoppers.

Example

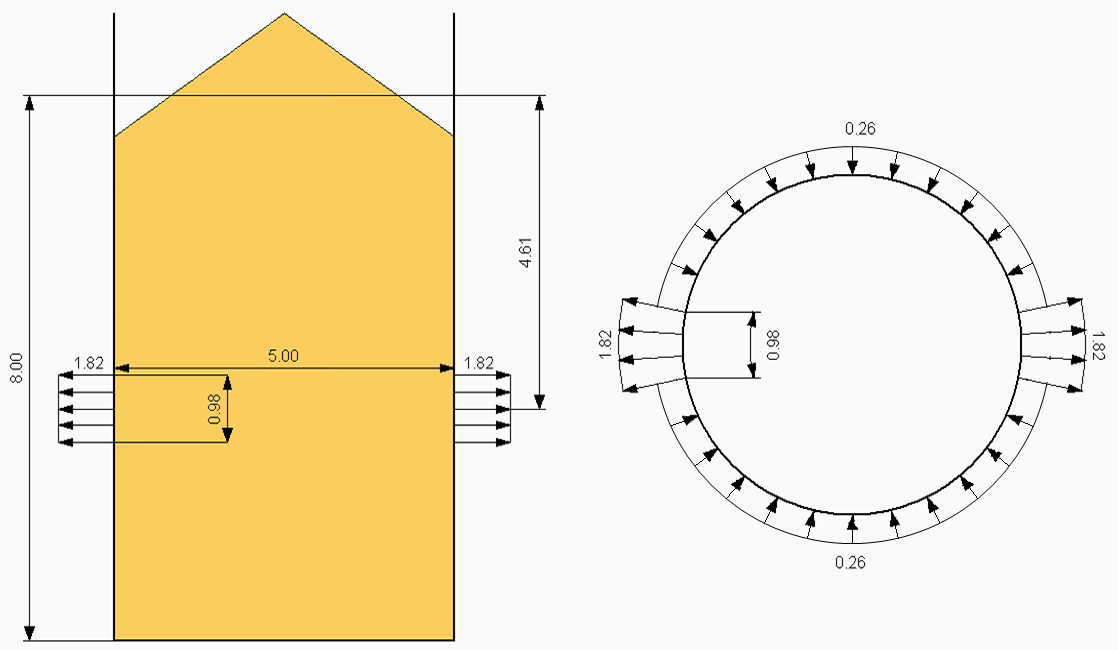
The example presents a free-standing cylindrical silo for cement with a diameter of 5.00 m and a maximum bulk unit depth of 8.00 m. The silo is made of reinforced concrete with a wall thickness of 0.30 m.

System and Component Dimensions of Cement Silo

Bulk Material
The following parameters for bulk solids were taken from Table E.1 of [1].

unit weight (upper) γ_u = 16.00 kN/m³
angle of repose Φ_r = 36.00°
angle of internal friction (mean) Φ_im = 30.00°
conversion factor a_φ = 1.22
lateral pressure ratio (mean) Κ_m = 0.54
conversion factor a_Κ = 1.20
wall friction coefficient (wall type D3) μ_m = 0.51 (for concrete)
conversion factor a_μ = 1.07
characteristic value for patch load C_op = 0.50

Characteristic Properties of Bulk Solids
In order to determine the characteristic values of the lateral pressure ratio, wall friction coefficient, and angle of internal friction, the listed mean values of the particulate solids must be scaled using the conversion factors. The conversion factors a_x are specified in Table E.1 of [1] for the available particulate solids.

Upper and lower characteristic values of the lateral pressure ratio
Κ_u = a_Κ ∙ Κ_m = 1.20 ∙ 0.54 = 0.648
Κ_l = Κ_m / a_Κ = 0.54 / 1.20 = 0.450

Upper and lower characteristic values of the wall friction coefficient
μ_u = a_μ ∙ μ_m = 1.07 ∙ 0.51 = 0.546
μ_l = μ_m / a_μ= 0.51 / 1.07 = 0.477

Upper and lower characteristic values of the angle of internal friction
Φ_iu = a_Φ ∙ Φ_im = 1.22 ∙ 30.00° = 36.60°
Φ_iu = Φ_im / a_Φ = 30.00° / 1.22 = 24.59°

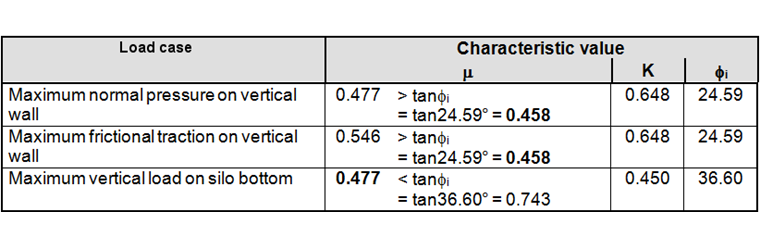
Governing characteristic values for different load applications
The evaluation of each load case should be made using a single set of consistent values of the solids properties, so that each limit state corresponds to a single defined stored solid condition. The extreme values of solids properties that should be adopted for each load case is given in the following table.

Relevant Parameters for Different Load Applications

The angle of wall friction must always be less than or equal to the angle of internal friction of the stored solid; that is, Φ_wh ≤ Φ_i. Otherwise, the material will rupture internally if slip at the wall contact demands a greater shear stress than the internal friction can sustain. This means that, in all cases, the wall friction coefficient should not be taken as greater than tanΦ_i (μ = tanΦ_w ≤ tanΦ_i). This is considered in the table above, where the relevant values are in bold.

Actions
The actions are determined on the basis of DIN EN 1991-4 1. Only the filling loads on vertical walls and the vertical pressures on the flat bottoms of the silo should be calculated here.

Silo Classification
The classification of the silo is based on the slenderness and the action assessment class.

Slenderness
1.0 < h_c / d_c = 8.00 / 5.00 = 1.6 < 2.0
The silo is classified as an intermediate slenderness silo in accordance with 1.5.21 of [1].

Action Assessment Class
Capacity = V ∙ γ_u = 157.08 ∙ 16.00 = 2513.27 ≙ 2513.27 / 9.80665 = 256.28 t
According to Table 2.1 of [1], at least Action Assessment Class 2 must be selected.

Construction Form
d_c / t = 5.00 / 0.30 = 16.7 < 200
The silo is classified as a thick‑walled silo in accordance with 1.5.43 of EN 1991‑4 [1].

Symmetrical Filling Loads on Vertical Silo Walls

Horizontal Pressure
Janssen characteristic depth z_o

z_{o} = \frac{1}{K \cdot μ} \cdot \frac{A}{U} = \frac{1}{0.648 \cdot 0.458} \cdot \frac{19.63}{15.71} = 4.22 m (5.75)

Formula 1

Vertical Distance h_o
For a symmetrically filled circular silo, the vertical distance h_o between the equivalent surface of the solid and the highest solid‑wall contact is calculated as follows:

h_{o} = \frac{d_{c} \cdot {tanΦ}_{r}}{6} = \frac{5.00 \cdot \tan 36.00 °}{6} = 0.61 m (5.77)

Formula 2

Parameter n

n = - (1 {tanΦ}_{r}) \cdot (1 - \frac{h_{o}}{z_{o}}) = - (1 \tan 36.00 °) \cdot (1 - \frac{0.61}{4.22}) = - 1.48 (5.76)

Formula 3

Asymptotic Horizontal Pressure at Great Depth Due to Stored Bulk Solids p_ho
p_ho = γ ∙ K ∙ z_o = 16.00 ∙ 0.648 ∙ 4.22 = 43.70 kN/m² (5.73)

Horizontal Pressure p_hf(z)

p_{hf} (z) = p_{ho} \cdot Y_{R} (z) = p_{ho} \cdot (1 - {(\frac{z - h_{o}}{z_{o} - h_{o}} 1)}^{n}) (5.71)

Formula 4

p_hf(0.61) = 0 kN/m²
p_hf(1.61) = 13.26 kN/m²
p_hf(2.61) = 20.93 kN/m²
p_hf(3.61) = 25.83 kN/m²
p_hf(4.61) = 29.19 kN/m²
p_hf(5.61) = 31.62 kN/m²
p_hf(6.61) = 33.43 kN/m²
p_hf(7.61) = 34.83 kN/m²
p_hf(8.00) = 35.29 kN/m²

Wall Frictional Traction
Janssen characteristic depth z_o

z_{o} = \frac{1}{K \cdot μ} \cdot \frac{A}{U} = \frac{1}{0.648 \cdot 0.458} \cdot \frac{19.63}{15.71} = 4.22 m (5.75)

Formula 1

Vertical distance h_o
For a symmetrically filled circular silo, the vertical distance h_o between the equivalent surface of the solid and the highest solid‑wall contact is calculated as follows:

h_{o} = \frac{d_{c} \cdot {tanΦ}_{r}}{6} = \frac{5.00 \cdot \tan 36.00 °}{6} = 0.61 m (5.77)

Formula 2

Parameter n

n = - (1 \tan Φ_{r}) \cdot (1 - \frac{ho}{zo}) = - (1 \tan 36.00 °) \cdot (1 - \frac{0.61}{4.22}) = - 1.48 (5.76)

Formula 5

Asymptotic horizontal pressure at a great depth from stored bulk material p_ho
p_ho = γ ∙ K ∙ z_o = 16.00 ∙ 0.648 ∙ 4.22 = 43.70 kN/m² (5.73)

Wall frictional traction p_wf(z)

p_{wf} (z) = μ \cdot p_{ho} \cdot Y_{R} (z) = μ \cdot p_{ho} \cdot (1 - {(\frac{z - h_{o}}{z_{o} - h_{o}} 1)}^{n}) (5.72)

Formula 6

p_wf(0.61) = 0 kN/m²
p_wf(1.61) = 6.07 kN/m²
p_wf(2.61) = 9.58 kN/m²
p_wf(3.61) = 11.82 kN/m²
p_wf(4.61) = 13.36 kN/m²
p_wf(5.61) = 14.47 kN/m²
p_wf(6.61) = 15.30 kN/m²
p_wf(7.61) = 15.94 kN/m²
p_wf(8.00) = 16.15 kN/m²

Vertical Pressure
Janssen characteristic depth z_o

z_{o} = \frac{1}{K \cdot μ} \cdot \frac{A}{U} = \frac{1}{0.450 \cdot 0.477} \cdot \frac{19.63}{15.71} = 5.83 m (5.75)

Formula 7

Parameter n

n = - (1 \tan Φ_{r}) \cdot (1 - \frac{h_{o}}{zo}) = - (1 \tan 36.00 °) \cdot (1 - \frac{0.61}{5.83}) = - 1.55 (5.76)

Formula 8

Vertical pressure p_vf(z)

p_{vf} (z) = γ \cdot z_{v} (z) = γ \cdot (h_{o} - \frac{1}{n 1} \cdot (z_{o} - h_{o} - \frac{(z z_{o} - 2 \cdot h_{o})^{n 1}}{(z_{o} - h_{o})^{n}})) (5.79)

Formula 9

p_vf(0.61) = 9.69 kN/m²
p_vf(1.61) = 23.65 kN/m²
p_vf(2.61) = 34.51 kN/m²
p_vf(3.61) = 43.27 kN/m²
p_vf(4.61) = 50.52 kN/m²
p_vf(5.61) = 56.65 kN/m²
p_vf(6.61) = 61.92 kN/m²
p_vf(7.61) = 66.50 kN/m²
p_vf(8.00) = 68.15 kN/m²

Vertical forces (compressive) in the wall n_zSk(z)
n_zSk(z) = μ ∙ p_ho(z) ∙ (z - z_v) (5.81)
n_zSk(0.61) = 0.00 kN/m
n_zSk(1.61) = 2.55 kN/m
n_zSk(2.61) = 8.97 kN/m
n_zSk(3.61) = 18.02 kN/m
n_zSk(4.61) = 28.96 kN/m
n_zSk(5.61) = 41.30 kN/m
n_zSk(6.61) = 54.72 kN/m
n_zSk(7.61) = 68.98 kN/m
n_zSk(8.00) = 74.81 kN/m

Asymmetric Filling Loads on Vertical Silo Walls

Dimension of the patch load zone

s = \frac{π \cdot d_{c}}{16} = \frac{π \cdot 5.00}{16} = 0.98 m (5.12)

Formula 10

Characteristic depth z_o according to the Janssen theory

z_{o} = \frac{1}{K \cdot μ} \cdot \frac{A}{U} = \frac{1}{0.648 \cdot 0.458} \cdot \frac{19.63}{15.71} = 4.22 m (5.75)

Formula 1

h_{o} = \frac{d_{c} \cdot {tanΦ}_{r}}{6} = \frac{5.00 \cdot \tan 36.00 °}{6} = 0.61 m (5.77)

Formula 2

Parameter n

n = - (1 \tan Φ_{r}) \cdot (1 - \frac{h_{o}}{z_{o}}) = - (1 \tan 36.00 °) \cdot (1 - \frac{0.61}{4.22}) = - 1.48 (5.76)

Formula 11

Asymptotic Horizontal Pressure at Great Depth Due to Stored Bulk Solids p_ho
p_ho = γ ∙ K ∙ z_o = 16.00 ∙ 0.648 ∙ 4.22 = 43.70 kN/m² (5.73)

Load increase factor C_pf of the partial area load for the filling load case

\begin{array}{l} E = 2 \cdot \frac{e_{f}}{d_{c}} = 2 \cdot \frac{0.00}{5.00} = 0.00 (5.10) \\ C_{pf} = 0.21 \cdot C_{op} \cdot (1 2 \cdot E ²) \cdot (1 - e^{- 1.5 \cdot (\frac{h_{c}}{d_{c}} - 1)}) = 0.21 \cdot 0.50 \cdot (1 2 \cdot 0.002) \cdot (1 - e^{- 1.5 \cdot (\frac{8.00}{5.00} - 1)}) = 0.06 \geq 0 (5.9) \end{array}

Formula 12

Patch load for the filling load case

p_{pf} (z) = C_{pf} \cdot p_{hf} (z) = C_{pf} \cdot p_{ho} \cdot Y_{R} (z) = C_{pf} \cdot p_{ho} \cdot (1 - {(\frac{z - h_{o}}{z_{o} - h_{o}} 1)}^{n}) (5.8)

Formula 13

p_pf(0.61) = 0 kN/m²
p_pf(1.61) = 0.83 kN/m²
p_pf(2.61) = 1.30 kN/m²
p_pf(3.61) = 1.61 kN/m²
p_pf(4.61) = 1.82 kN/m²
p_pf(5.61) = 1.97 kN/m²
p_pf(6.61) = 2.08 kN/m²
p_pf(7.61) = 2.17 kN/m²
p_pf(8.00) = 2.20 kN/m²

p_{pfi} (z) = \frac{p_{pf} (z)}{7} (5.13)

Formula 14

p_pfi(0.61) = 0 kN/m²
p_pfi(1.61) = 0.12 kN/m²
p_pfi(2.61) = 0.19 kN/m²
p_pfi(3.61) = 0.23 kN/m²
p_pfi(4.61) = 0.26 kN/m²
p_pfi(5.61) = 0.28 kN/m²
p_pfi(6.61) = 0.30 kN/m²
p_pfi(7.61) = 0.31 kN/m²
p_pfi(8.00) = 0.31 kN/m²

Loads on horizontal silo floors

Vertical pressure acting on flat bottoms of intermediate slenderness silos cannot be taken as uniform, and the calculation is based on the following load assessments:

\begin{array}{l} C_{b} = 1.0 (6.3) \\ p_{vb} = C_{b} \cdot p_{vf} (hc) = 1.0 \cdot 68.15 = 68.15 kN / m ² (6.2) \\ h_{tp} = \tan Φ_{r} \cdot \frac{d_{c}}{2} = \tan 36.00 ° \cdot \frac{5.00}{2} = 1.82 m (Figure 6.3) \\ p_{vtp} = γ \cdot h_{tp} = 16.00 \cdot 1.82 = 29.06 kN / m ² (6.15) \\ p_{vho} = γ \cdot z_{v} = 16.00 \cdot 0.61 = 9.69 kN / m ² (5.79) \\ {Δp}_{sq} = p_{vtp} - p_{vho} = 29.06 - 9.69 = 19.37 kN / m ² (6.14) \\ p_{vsq} = p_{vb} {Δp}_{sq} \cdot \frac{2.0 - \frac{h_{c}}{d_{c}}}{2.0 - \frac{h_{tp}}{d_{c}}} = 68.15 19.37 \cdot \frac{2.0 - \frac{8.00}{5.00}}{2.0 - \frac{1.82}{5.00}} = 72.89 kN / m ² (6.13) \end{array}

Formula 15

The bottom load magnifying factor Cb applies to silos of Action Assessment Class 2 under the condition that the stored solids do not tend toward dynamic behavior during the discharge process.
The vertical pressure p_vsq on the bottom of a silo may be taken to act both after filling and during discharge.

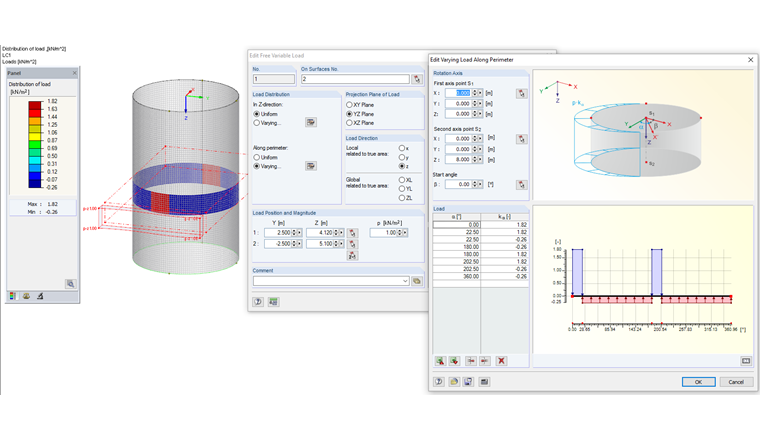
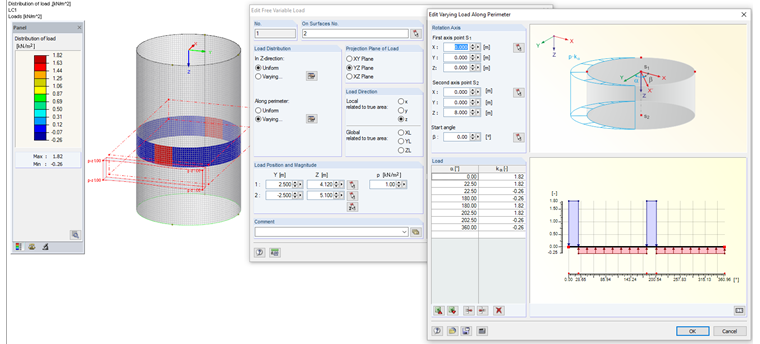
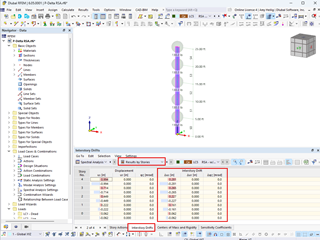
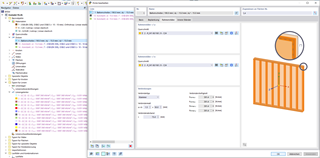
Entering Loads in RFEM

The defined load can be entered in RFEM. Figure 13 shows the exemplary filling patch load for z = 4.61 m. This load can be entered in RFEM as a free variable load. The load input is displayed in Figure 14.

Partial Surface Load for Load Case Filling (z = 4.61 m)

Load Input in RFEM for Partial Surface Load for Load Case Filling (z = 4.61 m)

Literature

[1] Eurocode 1: Actions on Structures - Part 4: Silos and Tanks; EN 1991‑4:2010‑12

Author

Ms. von Bloh provides technical support for our customers and is responsible for the development of the SHAPE‑THIN program as well as steel and aluminum structures.

Links

Analysis & Design Software for Silos and Storage Tanks

Downloads

RFEM Model File

356 KB

Do you have any questions?

Events

2024-04-24

Online Training

RFEM 6 | Students | Introduction to FEM

2024-04-25

Stiffening Design in RFEM 6 Using Building Model

Webinar

Stiffening Design in RFEM 6 Using Building Model

2024-04-25

AISC 360-22 Steel Connection Design in RFEM 6

Webinar

AISC 360-22 Steel Connection Design in RFEM 6 (USA)

2024-04-30

Online Training

RFEM 6 | Students | Introduction to Timber Design

2024-05-02

Construction Stages in Membrane Structures with RFEM 6

Webinar

Construction Stages in Membrane Structures with RFEM 6

2024-05-08

Online Training

RFEM 6 | Students | Introduction to Reinforced Concrete Design

2024-05-08

$Cross-Section Modeling and \n Stress Analysis in RSECTION 1$

Webinar

Cross-Section Modeling and Stress Analysis in RSECTION 1

2024-05-15

Online Training

RFEM 6 | Students | Introduction to Steel Design

2024-05-16

Consideration of Construction Stages in RFEM 6

Webinar

Consideration of Construction Stages in RFEM 6

2024-05-23

Most Frequently Asked Questions Answered by Dlubal Support Team

Webinar

Most Frequently Asked Questions Answered by Dlubal Support Team | May 2024

2024-05-29

$Steel Structures in RFEM 6 \n Part 1: Modeling, Load Input$

Webinar

Modeling and Design of Steel Structures in RFEM 6 | Part 1: Modeling, Load Input

2024-06-06

$Steel Structures in RFEM 6 \n Part 2: Combinations, Design, Documentation$

Webinar

Modeling and Design of Steel Structures in RFEM 6 | Part 2: Combinations, Design, Documentation

Videos

Knowledge Base

KB 000896 | Consideration of Eaves Area Formation when Generating Wind Load

Length: 00:01:00 min

General

Wind Loads on Buildings

Length: 00:03:27 min

General

What are Actions?

Length: 00:02:32 min

Knowledge Base

KB 000819 | Combinations of Crane Loads: EN 1990 + EN 1991-3; Cranes

Length: 00:00:38 min

Knowledge Base

KB 000771 | Considering Snow Drift

Length: 00:00:54 min

Knowledge Base

KB 000675 | Wind Load for Flat Roofs on Duopitch Roof

Length: 00:01:16 min

FAQ

[EN] FAQ 002008 | How can I apply wind load distribution to a cylinder according to EN 1991‑4, Section ...

Length: 00:01:00 min

Knowledge Base

KB 001667 | Combination of Actions for Road Bridges According to EN 1991-2

Length: 00:00:00 min

Knowledge Base

KB 001453 | Determination of Internal Pressure Coefficient (cpi)

Length: 00:00:25 min

Playlist

Models to Download

Model 004711 | Amphitheater of Theater in Most, Czech Republic

132x

Membrane roofing of the amphitheater

Concrete Building with Wind Load on Eaves Area

1144x

71x

Concrete Building with Wind Load on Eaves Area

890x

157x

Steel Hall

1333x

172x

Road Bridge with Two Lanes

1015x

Building in Nashville

1209x

31x

Building in New York

Model 004859 | Steel Structure | AISC 360/341-22

182x

22x

Steel Structure | AISC 360/341-22

69x

Steel Member RSA | ASCE 7 and NBC

3176x

209x

Steel Structure Column Base

Knowledge Base Articles

Consideration of Eaves Area Formation when Generating Wind Load

In addition to the geometry and shape of a flat roof, you can also take into account the formation of an eaves area when generating the loading.

Combinations of Crane Loads: EN 1990 + EN 1991-3; Cranes

The automatic creation of combinations in RFEM and RSTAB with the "EN 1990 + EN 1991‑3; Cranes" option allows you to design crane runway beams as well as support loads on the rest of the structure.

In RFEM and RSTAB, snow drift is considered according to 5.3.4(3) of DIN EN 1991‑1‑3 for saw-tooth roofs.

The Eurocode for DIN EN 1991‑1‑4:2010‑12 describes wind loads acting on structural systems.

Screenshots

Display of Silo Cells with Names of Geometric Parameters and Loads, Source: DIN EN 1991-4

Wall Surface Categories, Source: DIN EN 1991-4

Relevant Parameters for Different Load Applications, Source: DIN EN 1991-4

Classification of Design Situations, Source: DIN EN 1991-4

Silo Pressure Distribution Depending on Slenderness of Silo

Application of Partial Surface Loads, Source: DIN EN 1991-4

Flow Channel and Pressure Distribution for Silos with Large Discharge Eccentricities, Source: DIN EN 1991-4

Load Approaches for Silos with Large Discharge Eccentricities, Source: DIN EN 1991-4

Filling Pressures for Eccentrically Filled Low or Medium-Slender Silos, Source: DIN EN 1991-4

Product Features

Snow Load Generation According to EN 1991-1-3

There are load generators available for beam structures, creating snow loads according to ASCE/SEI 7-10. The load cases are generated depending on the roof shape. Another generator creates coating loads (ice). You can save recurring load combinations as templates.

Generate Snow Load According to Eurocode

The snow load generator can generate snow loads as member loads or surface loads.

Additional snow loads such as drifted snow loads, snow overhangs, and snow guards can be taken into account as well.

The following standards are available:

EN 1991-1-3 (incl. National Annexes)
DIN 1055-5
CTE DB-SE-AE
ASCE/SEI 7-16

More Information

Wind loads can be automatically generated as member loads or area loads on the following structural components (optional with internal pressure for open buildings):

Vertical walls
Flat roofs
Monopitch roofs
Duopitch/troughed roofs
Vertical walls with roof

The following standards are available:

EN 1991-1-3 (incl. National Annexes)
DIN 1055-4
CTE DB-SE-AE
ASCE/SEI 7-16

More Information

Use the "Independent mesh preferred" option in the FE mesh settings to create an independent FE mesh for the integrated objects. This allows you to generate a significantly more detailed and precise FE mesh for individual objects that are integrated into one another.

Frequently Asked Questions (FAQ)

The online service "Snow Load, Wind Speed, and Seismic Load Maps" displays the snow load zones 1*, 1a*, 2*, and 3* for Germany. Where are these snow load zones defined?

How can I apply wind load distribution to a cylinder according to EN 1991‑4, Section 7.9?

I noticed deviations from my sources in the online service "Snow Load, Wind Speed, and Seismic Load Maps". Where can I find information about the sources of your online service?

I noticed deviations from the map of DIN EN 1998‑1 or DIN 4149 in the online service "Geo-Zone Tool: Snow Load, Wind Speed, and Seismic Load Maps". Can you tell me which map is current and thus governing?

Are the models and presentations from Info Day 2020 freely available, and can you send them to me?

Which load direction should I select for members and surfaces in the case of a wind load?

Customer Projects