Settlement Calculation of Single Foundations According to DIN 4019 in RF-/FOUNDATION Pro

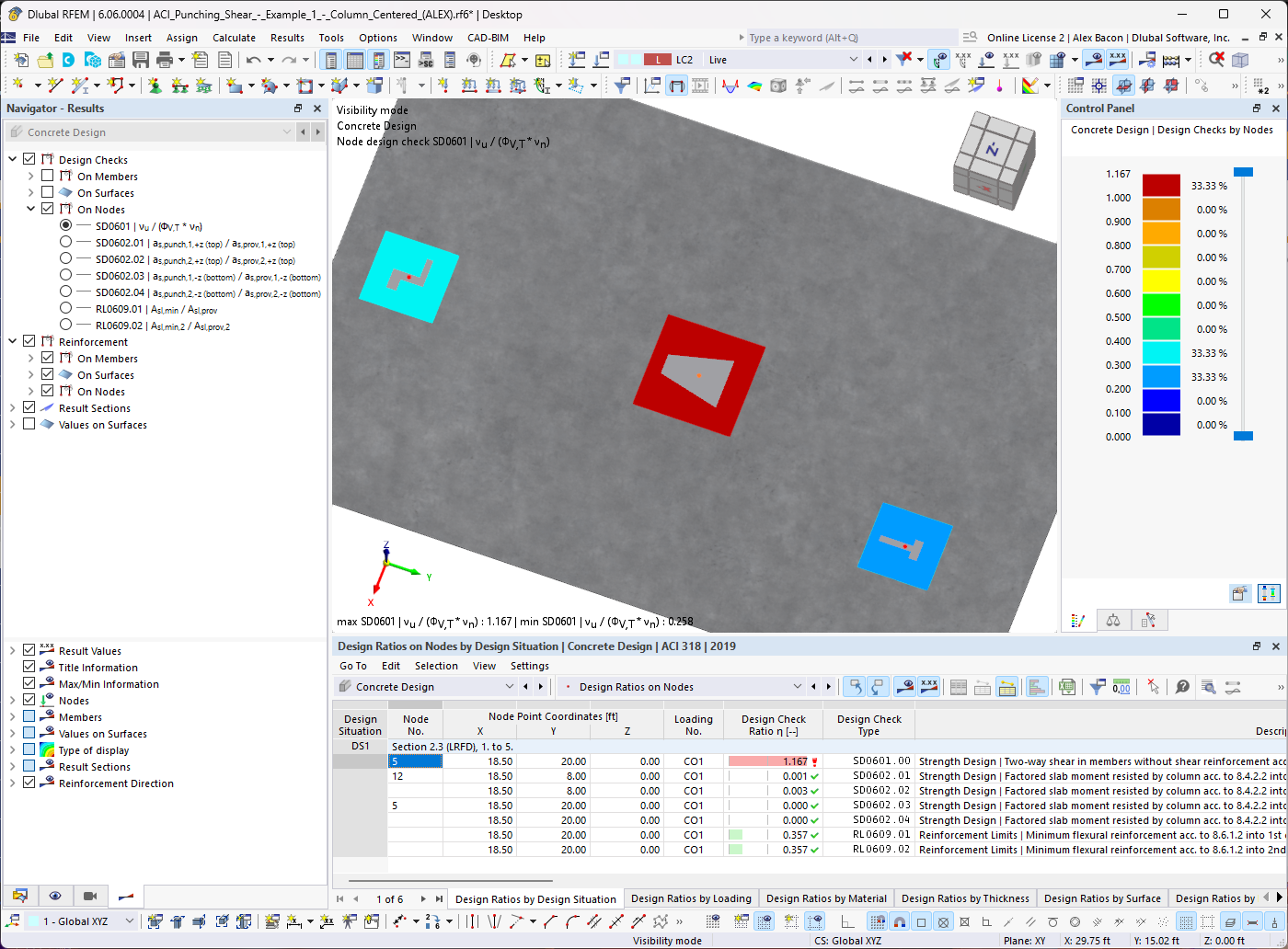
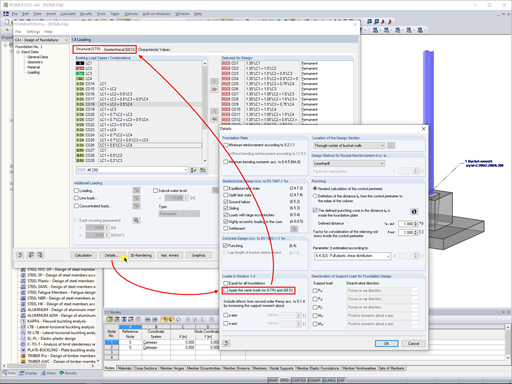
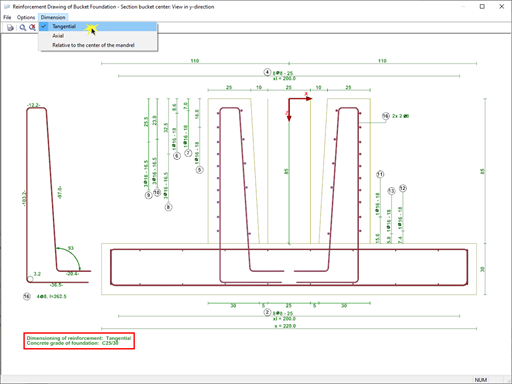
General

The total settlement s_tot on soil caused by structural loads consists of the components of the immediate settlement s₀, consolidation settlement s₁, and the time-dependent creep settlement s₂.

s_tot = s₀ + s₁ + s₂ = s + s₂

According to DIN 4019 [2], the method described below includes a specific setting "s" consisting of both settlement components – settlement caused by consolidation and settlement caused by creep (secondary settlement). Image 01 shows the time-dependent settlement components graphically. In this case, the time t₀ represents the period until complete consolidation occurs.

Time-Dependent Settlement Components [2]

Settlement Calculation Using Vertical Stresses on Soil

The settlement calculation method described below is based on the model of an elastic, isotropic, homogeneous half-space. This calculation approach can also be applied for the settlement of foundation soil with several layers.

To determine the settlement, it is necessary to divide the soil into strips and define the vertical soil stresses beneath the foundation base. Based on the elasticity analysis, the specific settlements s_i are determined for each strip; these are then added together to obtain the total settlement s.

Determination of Vertical Soil Stresses

First, the settlement calculation requires the determination of vertical soil stresses. The stress and settlement calculation is based on a model of the elastic isotropic half-space. The respective stresses can be distinguished according to their cause as follows:
σ_or is the soil stress caused by the soil self-weight
σ_z is the stress caused by a structural load
σ_z,i is the stress caused by the structural load in strip i

The vertical soil stresses σ_z due to the additional load at depth z can be calculated on the basis of the Boussinesq approach [3] and the superposition principle.

According to Boussinesq, the vertical stress on soil caused by the vertical concentrated load V is calculated on the half-space surface as shown in Image 02.

Vertical Soil Stress According to Boussinesq [2]

The vertical soil stresses at depth z under the corner point of a uniform "elastic" rectangle stress σ_z can be determined according to Image 03.

Vertical Soil Stress Under Corner Point of Uniform Rectangular Load [2]

The stress influence coefficient i_R can be deduced from the corresponding nomograms, for example from DIN 4019 [2].

By applying the approach mentioned above, you obtain the result of the vertical soil stress distribution on the soil under the foundation, which is symbolically represented in Image 04.

Distribution of Vertical Soil Stresses and Related Settlement Under Uniformly Distributed Load from [2]

Settlement Depth

In the settlement calculation, it is necessary to consider additional stresses due to the foundation load up to the influence depth of the settlement, also called limit depth. According to EN 1997-1 [1] and DIN 4019 [2], the settlement influence depth may be taken as the depth z, at which the effective vertical stresses due to the foundation load are 20% of the effective initial vertical stresses in the soil.