Example
The following load cases are available:
LC1 - Self-weight
LC2 - Snow
LC3 - Imposed load - alternative 1
LC4 - Imposed load - alternative 2
We are looking for the envelope of internal forces for ULS according to EN 1990. The imposed load cases may be taken into account in the combination.
Combination via Result Combinations
According to EN 1990, Eq. 6.10, the actions should be provided with partial safety factors and combination coefficients. However, you can only specify one factor when defining a result combination. Therefore, if it is not clear which variable action is the governing one, you should create several action combinations.
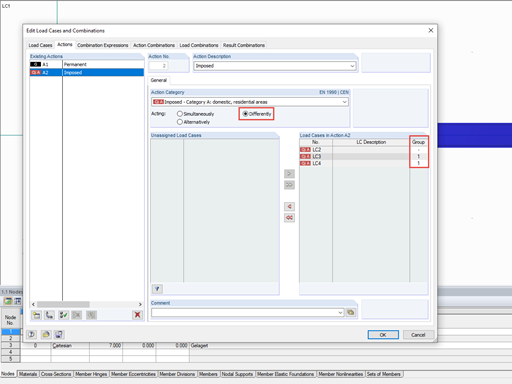
After assigning the factors, you should define a criterion and a group. The internal forces of the "self‑weight" should always apply and they are thus defined as "permanent". Other load cases may occur, but not necessarily. Therefore, the "Variable" criterion is assigned in this case. The specifics of the alternatively acting imposed load cases are controlled by the group. Both imposed load cases have the same number. Therefore, only one imposed load load case is used for the combination.
The final enveloping result combination is generated as follows:
RC3 (ULS) = RC1/s or RC2/s
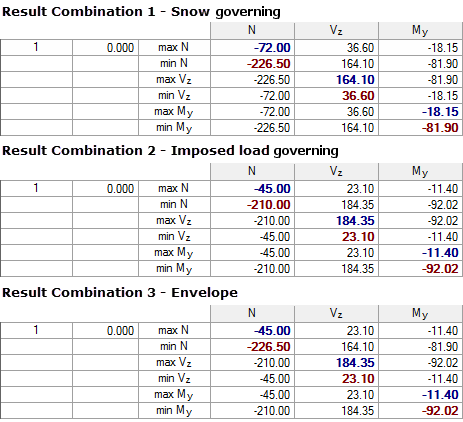
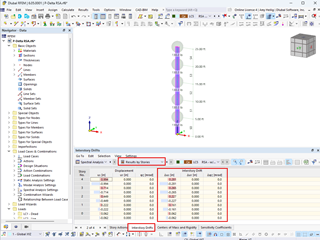
Based on this theoretical example, there are the following internal forces for RC1 and RC2 as well as the resulting internal forces for RC3:
Combination via Load Combinations
The same four load cases will now be superimposed using load combinations. In order to ensure that the most unfavourable internal forces are found, all possible combinations are created. These are also generated with regard to the predominantly variable loads as well as the alternative effects of the imposed loads. The basic requirement for the subsequent comparison with the result combinations is a linear system and the calculation of the load combinations according to the linear static analysis.
A total of eight load combinations are required. In order to compare the results with those of the result combinations, another enveloping RC is created, which includes the results of the load combinations:
RC4 = CO1/p or CO2/p or CO3/p or CO4/p or CO5/p or CO6/p or CO7/p or CO8/p
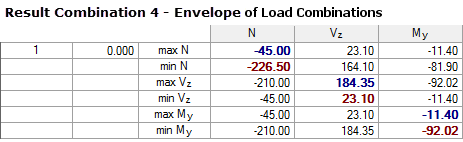
Based on the same system, we get the following internal forces:
Comparison of Results
If you compare the internal forces of RC3 and RC4, there are no differences found in this example. It is noteworthy, however, that it is necessary to create a total of nine combinations (8 LCs + 1 RC) in the case of the solution using load combinations, whereas the solution using result combination requires only three combinations. This saving effect has a positive influence on the calculation time, as well as on the overview in the program and especially in the report.
Summary
In geometrically linear models, which can be calculated according to the linear static analysis, result combinations represent an effective tool of combining load cases. It may be especially useful when analyzing a structure with a great number of load cases (motion loads, for example), which would otherwise lead to a high number of load combinations and thus make the documentation unclear.