Definition of Stress Losses from Relaxation for Prestressed Concrete Design

General

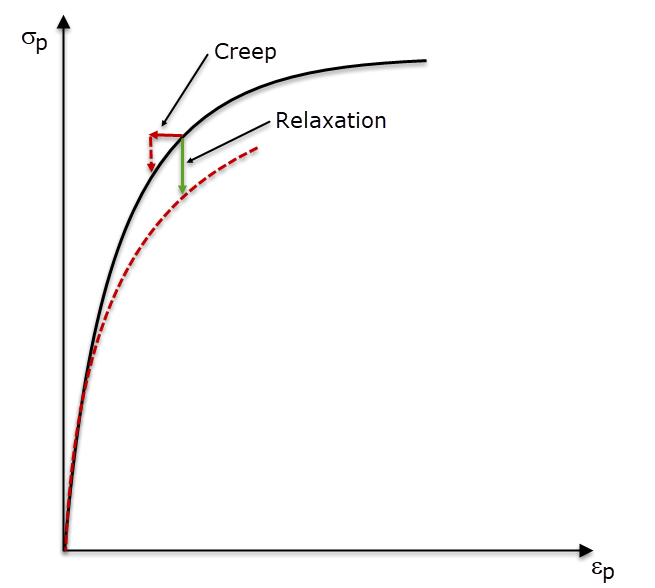
Creeping and shrinkage are time-dependent properties of concrete. While losses from concrete shrinkage are independent of loading, the applied pressure load plays a considerable role for creeping. Creeping represents an additional negative strain (compression) of the concrete at a constant compressive stress. Creeping and shrinkage cause a reduction of the applied tensile strain in the tendon due to the negative strain of the concrete cross-section.

Relaxation is a material property of prestressing steel and behaves inversely to concrete creeping. The term "relaxation" describes the reduction of the existing stress at a constantly applied material strain. Figure 01 graphically shows the influence of creeping and relaxation on the stress-strain diagrams of the prestressing steel.

Relaxation Losses According to EN 1992-1-1 [1]

The relaxation behavior of prestressing steels is determined according to the specifications of EN 15630 at a constant permanent temperature of 20 °C. Concerning the time- and stress-dependent relaxation behavior, the prestressing steels are classified in different classes. Cold-drawn wires and strands are currently manufactured with appropriate thermo treatment with low and very low relaxation. Prestressing bars are hot-rolled and hardened in most cases, and normally have higher relaxation losses.

The extent to which the stress losses from relaxation in prestressed concrete design have to be applied depends on the relevant valid design standard of the respective country. It may happen that a prestressing steel from a manufacturer in the European countries of Germany, Austria, or Switzerland has to be designed with different relaxation losses [4]. Eurocode 2 [1] classifies the prestressing steels in three different relaxation classes:

• Class 1: prestressing wires and strands with high relaxation
• Class 2: prestressing wires and strands with low relaxation
• Class 3: hot-rolled or hardened prestressing steel bars

In Chapter 3.3.2, calculation approaches are mentioned in EN 1992-1-1 [1], which allow determining relaxation-related prestressing steel losses dependent on the time after prestressing, the applied stress in the prestressing steel, and the reference value ρ₁₀₀₀. The reference value ρ₁₀₀₀ defines the relaxation losses after 1,000 hours of tension at an average temperature of 20 °C and a prestress of 0.7 ∙ f_p. f_p is here the actual, experimentally determined tensile strength of the prestressing steel. The reference values ρ₁₀₀₀ to be applied have to be taken either from the test report of the prestressing steel used or can be estimated with the values specified in [1]. Figure 02 shows the graphical distribution of the relaxation losses according to EN 1992-1-1, Section 3.3.2 for the three possible relaxation classes at a prestress of 0.7 ∙ f_pk.

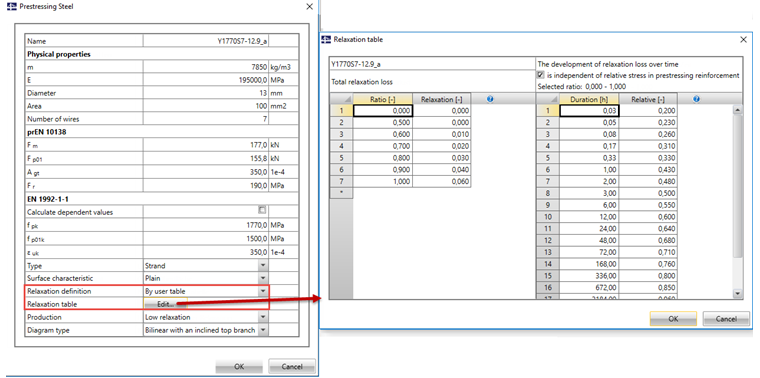
If a prestressing steel from the material library is selected in RF-TENDON, "By code" is preset at "Relaxation definition". This means that the calculation of the relaxation losses is based on the defined relaxation class according to EN 1992-1-1 [1] with Equations 3.28 to 3.30 and with the reference values ρ₁₀₀₀ estimated in [1] for the relaxation losses after 1,000 hours. In the left dialog box, Figure 03 shows a strand selected from the RF-TENDON material library with low relaxation. The preset relaxation class (Class 2) and the reference value ρ₁₀₀₀ = 2.5 are in line with the specifications in Chapter 3.3.2, Sections (6) to (7), from [1]. In the right dialog box of Figure 03, "By user ρ₁₀₀₀" has been selected for the relaxation definition. It is thus possible to define the relaxation class and the reference value ρ₁₀₀₀ from the approval of the prestressing steel. The time course of the relaxation losses is also defined in this input case according to Equations 3.28 to 3.30 from [1].

Relaxation Losses After Technical Approval of Prestressing Steel

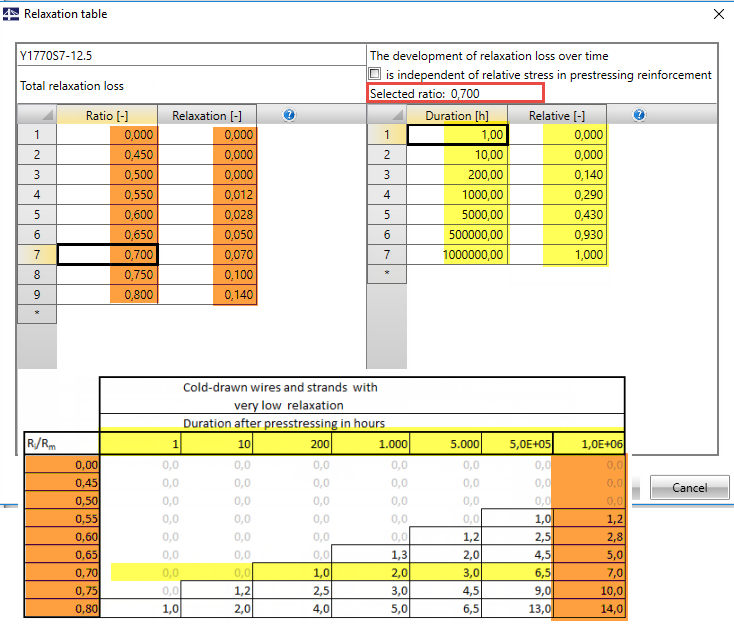
The German National Annex [2] to EN 1992-1-1 determines that losses from relaxation have to be taken from the technical approval of the prestressing steel. There are several options to specify the relaxation losses.

A common method in Europe to specify the stress losses from relaxation is the indication of two tables. The first table indicates the maximum relaxation losses at the point in time infinite (according to 3.3.2 [9] from [1], defining the final value for the point in time t = 500,000 hours is allowed), depending on the applied stress. A second table defines the time course of the relaxation losses as a ratio to the maximum stress loss from the first table. This split definition of relaxation losses also appears in RF-TENDON if the option "By user table" is selected at the input option for the relaxation definition. Here, the user has the option to define the time course as a global definition for all stress ratios (= a time table for the entire table of the total relaxation losses) or to define it separately as local input for each stress ratio (= a time table for each line of the table of the total relaxation losses). Figure 04 shows exemplarily the user-defined definition of the stress losses for a prestressing steel strand with low relaxation.

In Germany, it is also common to define the relaxation losses from the approvals of the prestressing steels in a matrix. The stress losses are indicated dependent on the applied prestressing steel stress and the durability. Figure 05 shows an extract of the German technical approval concerning prestressing steel Z-12.3-107.

To enter the matrix of the relaxation losses shown in Figure 05 into the two-part table of RF-TENDON, it is necessary to take the total stress losses from the last table of the matrix. In RF-TENDON, the time course of the relaxation losses has to be defined as a ratio to the maximum value. This means that the intermediate time values of the matrix have to be converted to relative values, related to the maximum value. Figure 05 shows the assignment of the matrix values in the single input tables of RF-TENDON.

At the end of this article, an Excel file is available for download that allows transforming the approval matrix to the two-part table automatically. The single tables can be exported to RF-TENDON using the clipboard. This tool simplifies the conversion of the relaxation matrix to the two-part table input.