Cross-Section Class Design
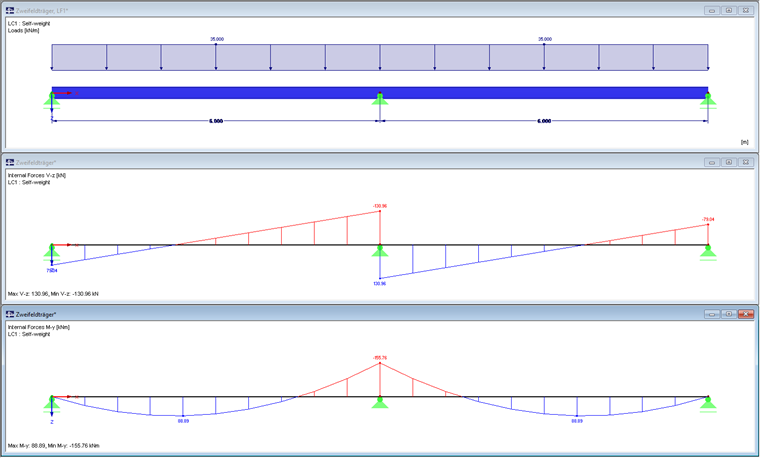
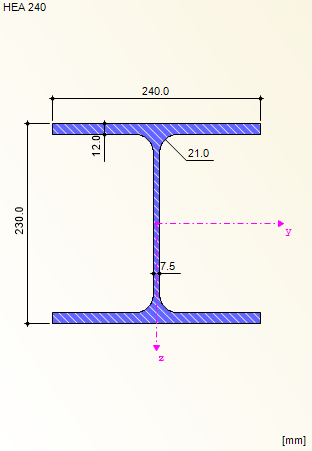
The area of the inner support of the two-span beam governs for designing the cross-section class and performing the cross-section design.
Design for the web (ψ = -1)
[1] Table 5.2, cross-section parts supported on two sides
The web thus fulfills the requirements of cross-section class 1.
Design for the bottom chord (ψ = 1)
[1] Table 5.2, cross-section parts supported on one side
The chords thus fulfill the requirements of cross-section class 2. The cross-section has to be assigned to cross-section class 2, because the class of the cross-section part that is evaluated as the most unfavorable will govern for the entire cross-section.
Shear Buckling of Web
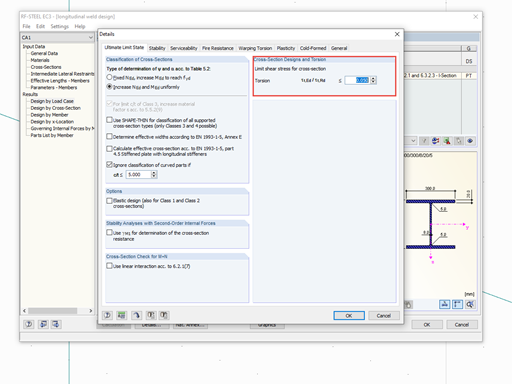
A check must be performed to learn if the shear buckling of the web has to be evaluated, regardless of the assignment of the cross-section class according to 6.2.6, Section (6) in [1]. The value η in Equation 6.22 in [1] is applied with 1.20.
According to EN 1993-1-5, Section 5, no shear buckling design is required.
Shear Designs
The cross-section design is carried out for a cross-section of class 2. Above the inner support, the beam is subjected to bending and shear force; at the location of the maximum sagging moment, only to bending. The influence of the M-V interaction is checked before determining the ultimate limit state of the structure. If VEd is not more than 0.5 ⋅ Vpl,Rd, reducing the moment resistance according to [1] Section 6.2.8 (2) is not required.
It is not necessary to reduce the moment resistance.
The following design has to be fulfilled for the design value of the acting bending moments MEd:
The design value of the bending stress of a cross-section, loaded with uniaxial bending, is determined as follows for cross-sections of class 2:








































.png?mw=600&hash=49b6a289915d28aa461360f7308b092631b1446e)