Theoretical Background
The vibrational motion of an initially undisturbed, then harmonically excited mechanical system consists of a damped natural vibration with decreasing amplitude and a forced vibration with constant amplitude. The transient process and the steady state are described in the following formula.
| t | Time |
| ω | Angular frequency of excitation |
| ωD | Angular frequency |
| ζ | Damping |
| A | Constant |
| B | Constant |
| C | Constant |
| D | Constant |
| η | Frequency ratio |
| γM0 | Partial safety factor for cross -section resistance |
| ωD | Angular frequency |
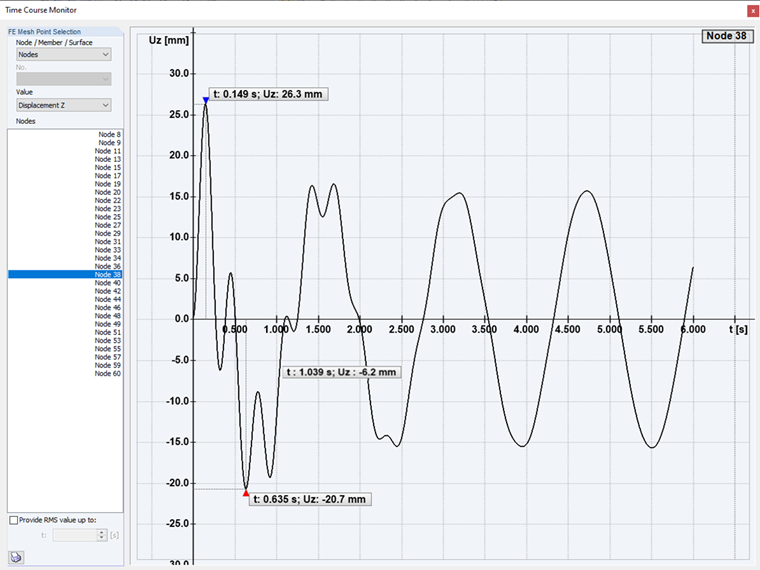
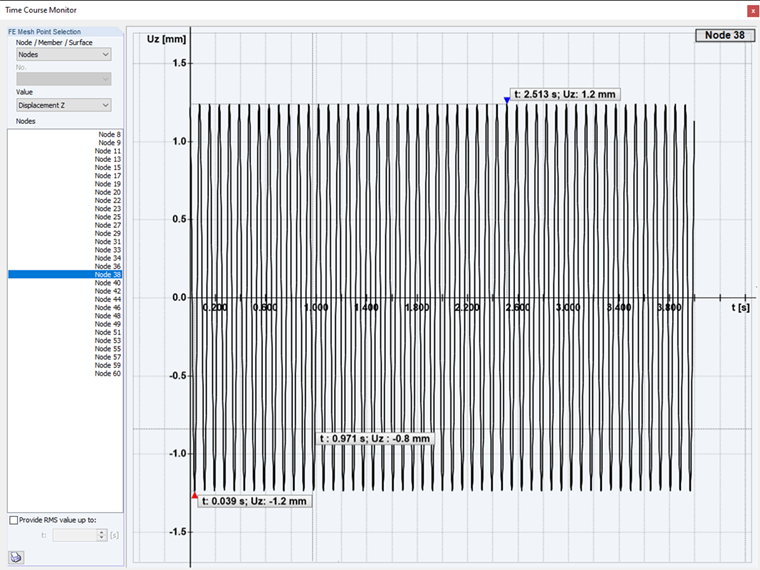
If this frequency ratio is η < 1, which is referred to as subcritical excitation, the forced vibration is slower than the damped natural vibration, and a transient process occurs. After a few fast periods of damped natural vibration, the system is tuned to the slower, forced vibration, which ultimately remains the only vibration component.
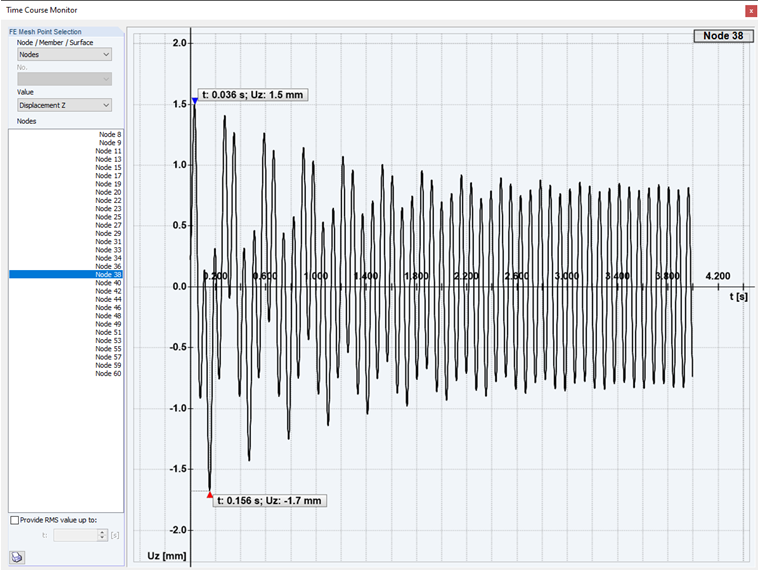
If the case is η > 1, now called supercritical excitation, the forced vibration is higher in frequency than the damped natural vibration. Now, fast harmonic oscillation takes place around the slower, damped natural oscillation until it has completely faded, and again only the vibration component forced by the excitation remains.
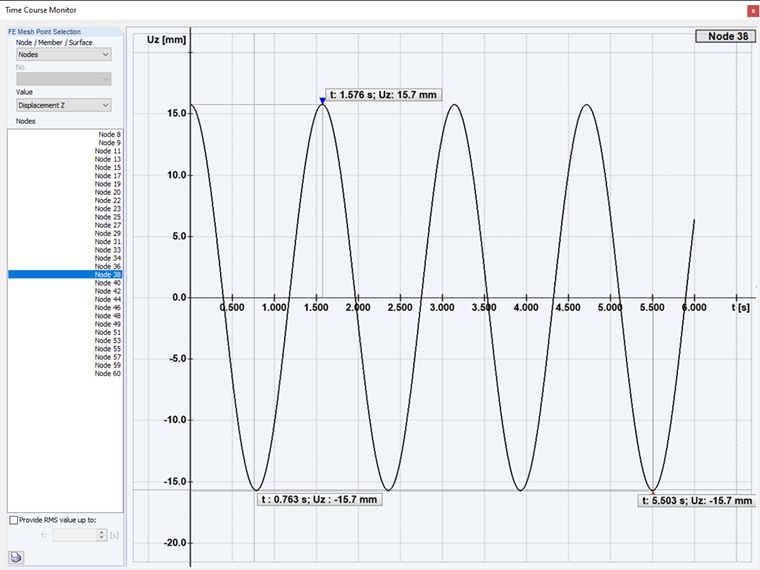
Since there is damping in all practically occurring cases, which leads to the natural vibration fading, it is only of interest, regardless of the frequency ratio, to consider and further analyze the respectively remaining forced vibration motion (steady-state part). This vibrational motion is called (quasi-) stationary vibration, and the corresponding state of the system is called steady state.
The natural vibration has the angular frequency ωD of the damped system, while the vibration component forced by excitation has the angular frequency ω of the harmonic excitation. Thus the overall vibration, which results from superpositioning these two partial vibrations, runs a course of which the appearance depends strongly on the ratio ω/ωD; that is, on the frequency ratio η.
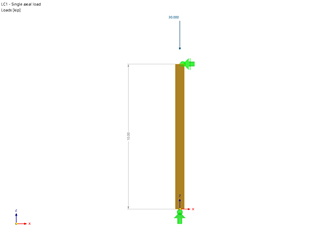
Example
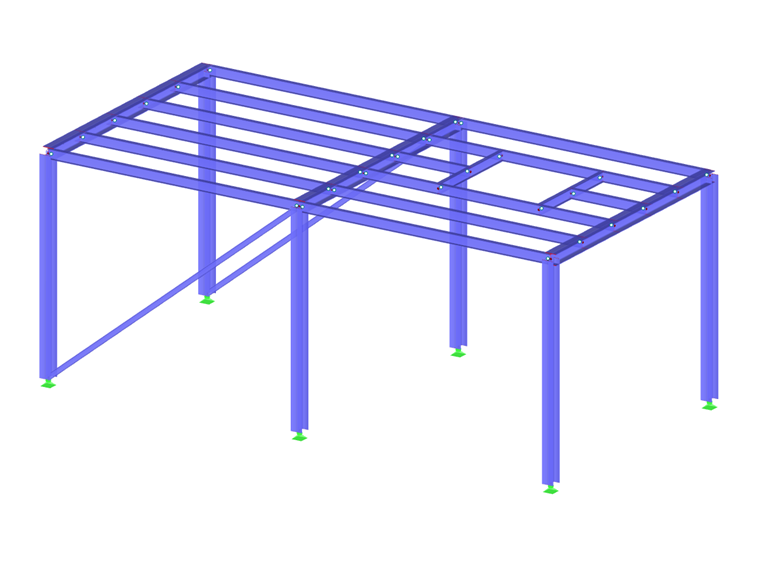
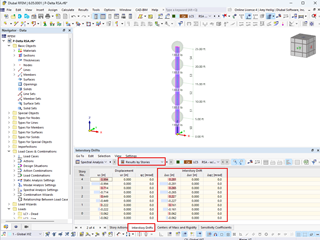
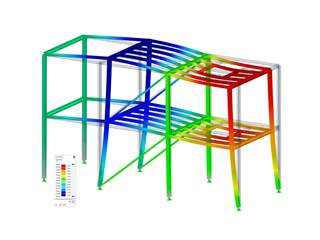
The transient behavior is described in the following text, using a steel structure. It is assumed that this structure is harmonically excited. In the structure, harmonic excitations are generated to show the different transient processes. In order to better attune the harmonic excitation's frequency to the structure, a natural vibration case is first created by means of the DYNAM Pro - Natural Vibrations add-on module. As a simplification, only mode shapes in the global Z-direction are considered in the natural vibration cases.
Subcritical excitation: In the first case of the time history analysis, a subcritical excitation of the structure is performed. With an excitation frequency lower than the mode shape.
Supercritical excitation: In the second case of the time history analysis, a supercritical excitation of the structure is performed. With an excitation frequency higher than the mode shape.
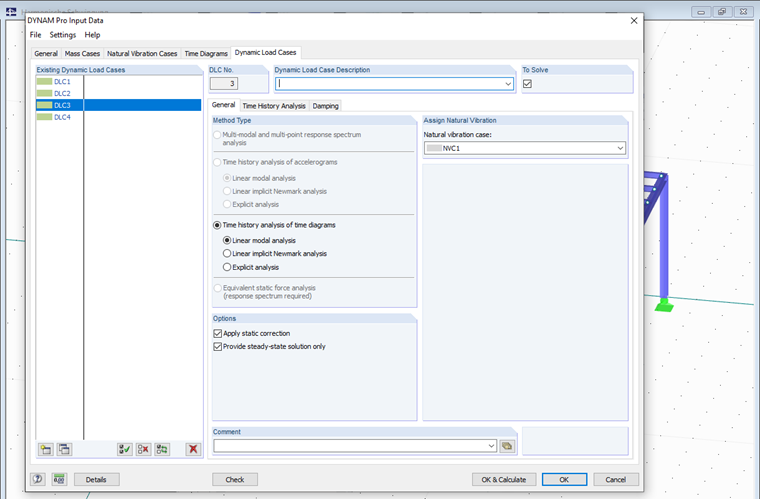
In the third and fourth cases, we use the add-on module option for a steady-state solution for both previously created excitation cases. In doing so, the stationary state is set directly. It is also generally referred to as steady state.





















_LI.jpg?mw=350&hash=3d52d6017982f88052836929c5d9b0ba0ab8104f)
_LI.jpg?mw=350&hash=3d52d6017982f88052836929c5d9b0ba0ab8104f)
_LI.jpg?mw=350&hash=3d52d6017982f88052836929c5d9b0ba0ab8104f)