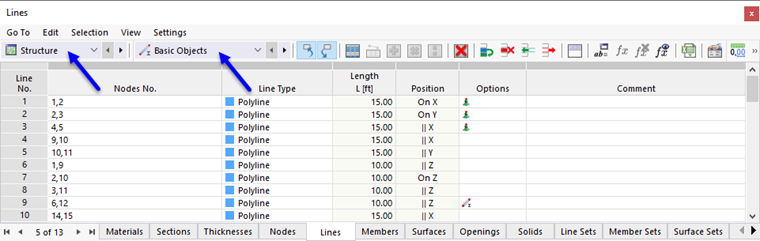
You find the tables at the bottom of the work window. They manage the model, load, and result data in numerical form.
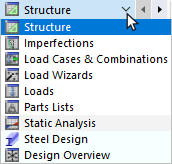
The table content can be controlled by means of categories, including individual sub-categories. First, define the category on the left in the table toolbar. The list provides various entries for structural, load, and result data.
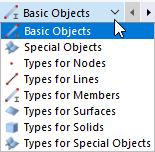
Then, select the sub-category in the list to the right. Each category is divided into specific entries.
You can now navigate to the individual tables using the tabs.
When you "grab" the tables with the pointer in their title bar, you can move them into the workspace. Double-clicking the title bar or moving it to the edge docks it back to the window frame.