No, it is not possible to deactivate the Mia assistant. However, if the avatar is in a distracting position, you can simply move it by using the mouse.
Our AI assistant is continuously being developed. In the future, Mia will become much more integrated in RFEM and it is learning new things every day. Our goal is to make your work with RFEM even more intuitive and easier.
Mia provides you with the opportunity to use the capabilities of large language models (LLM) for the structural analysis and program operation of RFEM 6 and RSTAB 9.
Mia already offers a number of advantages:
Support 24/7, including weekends
Perhaps you know this situation, too: a project that still needs to be finished. Shortly before the end, problems arise for which you urgently need support, and the phone support has already closed.
Mia can help you to find a solution to your problem in this situation.
Better work efficiency
You will get the answers to your problems directly. You don't need to interrupt your work until the support has responded to your question.
Communication in almost any language
Mia has an integrated translation function. Communicate in the language that is easiest for you.
Easy access to information
You don't need to search through long articles to finally get the information you are looking for. Instead, you get exactly the information that is relevant to your question.
Easy to use
Simply describe your problem in natural language. It's no longer necessary to formulate complicated Google search queries and to search in countless documents for the results.
User friendliness
The AI function of Mia is directly integrated into the program interface of RFEM 6 and RSTAB 9; that is, exactly where the questions arise. It is no longer necessary to switch to the browser and open a specific website.
Free access
With Mia, you get free, fast access to the support team.
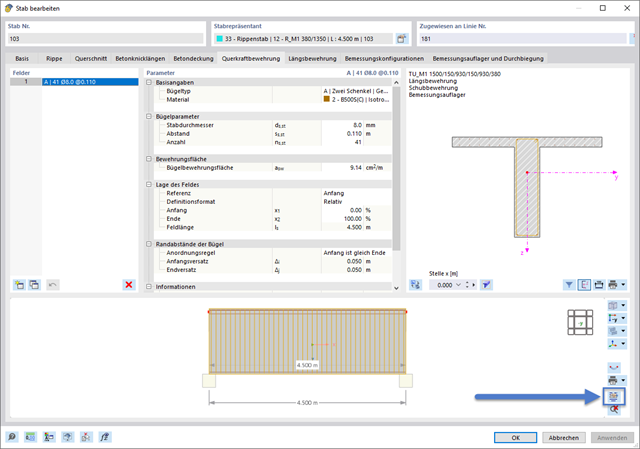
In the shortcut menu, you can find some important functions that support you when working with RFEM 6 and RSTAB 9.
Test Mia yourself. The answers are not always perfect, but are often amazingly good and effective. By the way, Mia also has a sense of humor.
More Information About Mia:
Show more