13929x

2018-06-27

Leggi dei materiali ortotropi

Le leggi dei materiali ortotropi sono utilizzate ovunque i materiali siano disposti in base al loro carico. Gli esempi includono plastica fibrorinforzata, lamiere trapezoidali, cemento armato e legno.

La legge di Hooke è solitamente inclusa per i materiali ortotropi

ν = \frac{E}{2 G} - 1 \leq 0, 5

Formula 1

- 1 < ν < 0, 5

Formula 2

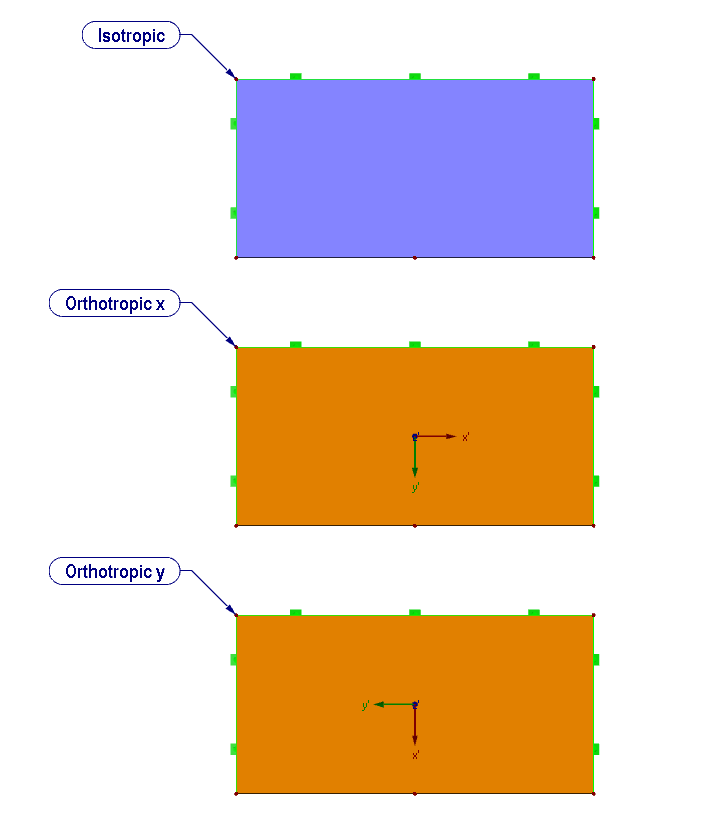
non è più valido.

deformazione trasversale

I seguenti parametri del materiale si riferiscono alle rigidezze bidimensionali e, se non diversamente indicato, al materiale del legno. La base è un sistema di assi locale, come mostrato nella Figura 01.

E_x = rigidezza nella direzione x locale della superficie
E y = rigidezza nella direzione locale y della superficie
G_xz = rigidezza a taglio nella direzione x locale della superficie (direzione dello spessore della piastra)
G_yz = rigidezza a taglio nella direzione locale y della superficie (direzione dello spessore della piastra)
G_xy = area nel piano di rigidezza a taglio
ν_xy = deformazione trasversale in direzione x
ν_yx = deformazione trasversale in direzione y

Le tensioni nella Figura 02 sono relative alle rigidezze qui menzionate.

tensioni tangenziali

La legge materiale è soggetta alle seguenti regole.

Equazione 1:

\frac{ν_{yx}}{E_{y}} = \frac{ν_{xy}}{E_{x}}

Formula 3

Equazione 2:

ν_{xy} ⩾ ν_{yx}

Formula 4

Equazione 3:

ν_{xy} = - \frac{ε_{y}}{ε_{x}} = \frac{E_{x}}{E_{y}} \cdot ν_{yx}

Formula 5

Equazione 4 (rigidezze nell'area nel piano):

[\begin{matrix} ε_{x} \\ ε_{y} \\ γ_{xy} \end{matrix}) = [\begin{matrix} \frac{1}{E_{x}} & - \frac{ν_{xy}}{E_{x}} & 0 \\ - \frac{ν_{xy}}{E_{x}} & \frac{1}{E_{y}} & 0 \\ 0 & 0 & G_{xy} \end{matrix}) \cdot [\begin{matrix} σ_{x} \\ σ_{y} \\ τ_{xy} \end{matrix})]]]

Formula 6

Il rapporto delle deformazioni nelle equazioni sopra menzionate sottolinea le relazioni nella Figura 01.

Le rigidezze nell'area nel piano sono calcolate come segue.

Equazione 5:

d_{i} = [\begin{matrix} d_{11, i} & d_{12, i} & 0 \\ d_{22, i} & 0 \\ sym & d_{33, i} \end{matrix}) = [\begin{matrix} \frac{E_{x, i}}{1 - ν_{xy, i}^{2} \frac{E_{y, i}}{E_{x, i}}} & \frac{ν_{xy, i} E_{y, i}}{1 - ν_{xy, i}^{2} \frac{E_{y, i}}{E_{x, i}}} & 0 \\ \frac{E_{y, i}}{1 - ν_{xy, i}^{2} \frac{E_{y, i}}{E_{x, i}}} & 0 \\ sym & G_{xy, i} \end{matrix})]]

Formula 7

Deformazione trasversale ν

Come spiegato nella Figura 01, le deformazioni e le tensioni modificate in questa direzione risultano dal comportamento più liscio del materiale nella rispettiva direzione.

Rapporto delle deformazioni:

Equazione 6:

ν_{xy} = - \frac{ε_{y}}{ε_{x}} \to ε_{y} = - ν_{x} \cdot ε_{x}

Formula 8

Equazione 7:

ν_{yx} = - \frac{ε_{x}}{ε_{y}} \to ε_{x} = - ν_{y} \cdot ε_{y}

Formula 9

Per

σ_{x} \neq 0, σ_{y} = 0, σ_{xy} = 0

Formula 10

le seguenti equazioni risultano con la legge di Hooke.

Equazione 8:

ε_{x} = \frac{σ_{x}}{E_{x}}

Formula 11

Equazione 9:

ε_{y} = \frac{σ_{y}}{E_{y}}

Formula 12

Equazione 10:

σ_{y} = ε_{y} \cdot E_{y} mit E_{y} = \frac{ν_{yx} \cdot E_{x}}{ν_{xy}} \to σ_{y} = ε_{y} \cdot \frac{ν_{yx} \cdot E_{x}}{ν_{xy}}

Formula 13

Equazione 11:

\to σ_{y} = ε_{y} \cdot \frac{ν_{yx} \cdot \frac{σ_{x}}{ε_{x}}}{ν_{xy}}

Formula 14

Equazione 12:

\to ε_{y} = \frac{ε_{y} \cdot \frac{ν_{yx} \cdot \frac{σ_{x}}{ε_{x}}}{ν_{xy}}}{E_{y}} mit ν_{xy} = - \frac{ε_{y}}{ε_{x}}

Formula 15

Equazione 13:

\to ε_{y} = \frac{ε_{y} \cdot ν_{yx} \cdot σ_{x}}{ε_{x} \cdot (- \frac{ε_{y}}{ε_{x}}) \cdot E_{y}} = - \frac{ν_{yx} \cdot σ_{x}}{E_{y}}

Formula 16

Matrice di rigidezza

Calcolo della matrice di rigidezza globale della piastra.

Equazione 14:

D = [\begin{matrix} D_{11} & D_{12} & 0 & 0 & 0 & 0 & 0 & 0 \\ D_{22} & 0 & 0 & 0 & 0 & 0 & 0 \\ D_{33} & 0 & 0 & 0 & 0 & 0 \\ D_{44} & 0 & 0 & 0 & 0 \\ D_{55} & 0 & 0 & 0 \\ sym & D_{66} & 0 & 0 \\ D_{77} & 0 \\ D_{88} \end{matrix})]

Formula 17

Componenti piegati:

Equazione 15:

D_{11} = \frac{d^{3}}{12} \cdot d_{11} \hat{=} \frac{E_{x} d^{3}}{12 (1 - ν_{xy} ν_{yx})}

Formula 18

Equazione 16:

D_{12} = \frac{d^{3}}{12} \cdot d_{12} \hat{=} sgn (ν_{xy}) \sqrt{ν_{xy} ν_{yx} D_{11} D_{22}}

Formula 19

Equazione 17:

D_{22} = \frac{d^{3}}{12} \cdot d_{22} \hat{=} \frac{E_{y} d^{3}}{12 (1 - ν_{xy} ν_{yx})}

Formula 20

Equazione 18:

D_{33} = \frac{d^{3}}{12} \cdot d_{33} \hat{=} G_{xy} \frac{d^{3}}{12}

Formula 21

Componenti della membrana:

Equazione 19:

D_{66} = d \cdot d_{11} \hat{=} \frac{E_{x} d}{1 - ν_{xy} ν_{yx}}

Formula 22

Equazione 20:

D_{67} = d \cdot d_{12} \hat{=} sgn (ν_{xy}) \sqrt{ν_{xy} ν_{yx} D_{66} D_{77}}

Formula 23

Equazione 21:

D_{77} = d \cdot d_{22} \hat{=} \frac{E_{y} d}{1 - ν_{xy} ν_{yx}}

Formula 24

Equazione 22:

D_{88} = d \cdot d_{33} \hat{=} G_{xy} d

Formula 25

Componenti di taglio:

Equazione 23:

D_{44} = \frac{5}{6} G_{xz} \cdot d

Formula 26

Equazione 24:

D_{55} = \frac{5}{6} G_{yz} \cdot d

Formula 27

Un prerequisito per queste equazioni è che la matrice di rigidezza sia definita positiva, cioè che tutti gli autovalori della matrice siano positivi.

Per questo motivo, RFEM verifica, tra le altre cose, la definizione della deformazione trasversale secondo la seguente equazione.

Equazione 25:

ν_{xy} \leq 0, 999 \cdot \sqrt{\frac{E_{x}}{E_{y}}}

Formula 28

Esempio

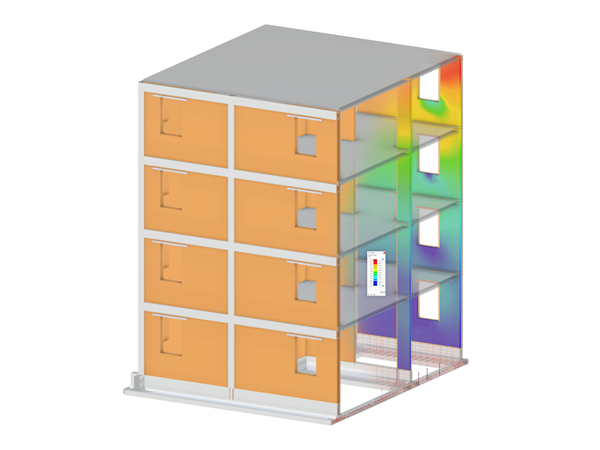
Il comportamento del materiale ortotropo sarà spiegato con il seguente esempio (Figura 03). Un materiale ortotropo sarà confrontato con un materiale isotropo. Inoltre, la rigidezza della piastra ortotropa sarà definita con l'elevata rigidezza nella direzione x e nella direzione y.

Sistema

Struttura:

Spessore piastra 200 mm
Materiale C 24
Rigidezze ortotrope

$\begin{array}{l} E_{x} = 1.100, 0 kN / {cm}^{2} \\ E_{y} = 37, 0 kN / {cm}^{2} \\ G_{y} = 6, 9 kN / {cm}^{2} \\ G_{x} = 69, 0 kN / {cm}^{2} \\ G_{xy} = 69, 0 kN / {cm}^{2} \\ ν_{xy} = 2, 52 \\ ν_{yx} = 0, 085 \end{array}$

Formula 29
Rigidezze isotrope

$\begin{array}{l} E = 1.100 kN / {cm}^{2} \\ G = 500 kN / {cm}^{2} \\ ν = 0, 1 \end{array}$

Formula 30
Dimensione w = 2,0 m, l = 4,0 m
Carico 20 kN/m²
Dimensione della maglia EF 50 cm

La struttura è vincolata rigidamente in direzione z verticale. Le condizioni del vincolo esterno nelle direzioni x e y sono state selezionate in modo tale che non si verifichino effetti dovuti al vincolo.

Il calcolo viene eseguito secondo l'analisi statica lineare con il comportamento elastico lineare del materiale e le condizioni del vincolo esterno.

La seguente deformazione trasversale risulta dalla legge di Hooke, insieme ai valori dati.

Equazione 26:

ν = (\sqrt{E_{x} \cdot E_{y}}) / (2 G) - 1 = 6, 97

Formula 31

Questa elevata deformazione trasversale è impossibile con il modello di materiale selezionato. Con le equazioni da [1] , i valori possono, tuttavia, essere modificati.

Equazione 27:

ν_{xy} \approx (\frac{\sqrt{E_{x} E_{y}}}{2 G_{xy}} - 1) \cdot \sqrt{\frac{E_{x}}{E_{y}}}

Formula 32

Equazione 28:

ν_{yx} \approx (\frac{\sqrt{E_{x} E_{y}}}{2 G_{xy}} - 1) \cdot \sqrt{\frac{E_{y}}{E_{x}}}

Formula 33

Equazione 29:

ν_{xy} = (\frac{\sqrt{1.100 \cdot 37}}{2 \cdot 69} - 1) \sqrt{\frac{1.100}{37}} = 2, 52

Formula 34

Equazione 30:

ν_{xy} = (\frac{\sqrt{1.100 \cdot 37}}{2 \cdot 69} - 1) \sqrt{\frac{37}{1.100}} = 0, 085

Formula 35

Superfici con rigidezze

Risultati:
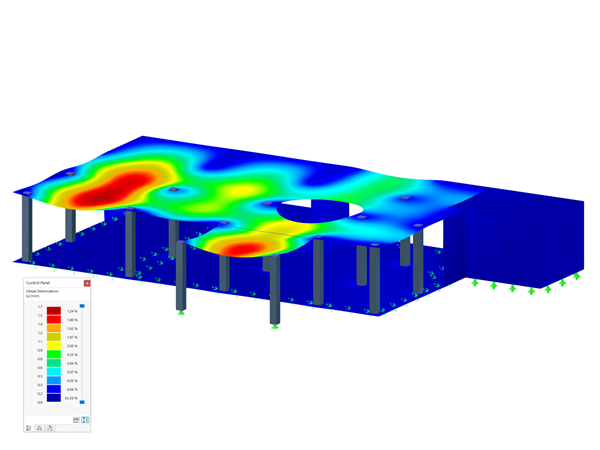
Come previsto, le deformazioni maggiori si verificano con l'orientamento delle rigidezze nella direzione y (Figura 06). La reazione del vincolo esterno e il momento della piastra isotropa sono visualizzati nella Figura 05.

Risultati materiale isotropo

Poiché la piastra con un'elevata rigidezza nella direzione y (E_y = 1.100 kN/cm²) ha un'elevata resistenza in questa direzione, anche le reazioni del vincolo esterno sono più elevate (125,4 kNm rispetto a 58,3 kNm).

Deformazioni e reazioni vincolari di placche ortotropiche

I momenti flettenti massimi risultanti per le piastre ortotrope sono uguali a m_x con la rigidezza in direzione x e per m_y con un'elevata rigidezza in direzione y.

Per la piastra con elevata rigidezza in direzione y, il momento flettente massimo m_y è quasi al centro della piastra (Figura 07).

Biegemomente der orthotropen Platte mx (links) und my (rechts)

Variazione della deformazione trasversale

La deformazione trasversale secondo i diagrammi di deformazione può raggiungere i valori massimo e minimo elencati nella tabella per un materiale di resistenza C24.

	Max.	Min.
ν_xy	5,447	-5,447
ν_yx	0,183	-0,183

La piastra introdotta all'inizio con l'elevata rigidezza (E_x = 11.000) sarà definita con queste elevate deformazioni trasversali per questo scopo. Le altre rigidezze della piastra, tuttavia, rimangono invariate.

La Figura 08 mostra i risultati della variazione di ν_xy = da 5,44 a -5,44.

Per ν_xy = 5.44, le reazioni del vincolo esterno sono qualitativamente identiche al comportamento isotropo del materiale. Il momento flettente aumenta da m_x = 18,1 kNm/m (piastra isotropa) a m_x = 34,9 kNm/m (piastra ortotropa).

Rispetto alla piastra ortotropa con deformazioni trasversali comuni (ν_xy = 2.5), il momento flettente è leggermente ridotto.

Ergebnisse der Variation gemäß Tabelle (links: νxy = 5,44, Centro: νxy = 0, a destra: νxy = -5,44)

Con ν_xy = 0, l'ampiezza elevata della reazione vincolare all'estremità libera della piastra viene spostata a un valore costante di 43 kN/m.

Il momento m_x aumenta a 38,1 kNm/m. Rispetto al risultato precedente (ν_xy =5.44), qui è mostrata l'influenza della deformazione trasversale. Per ν =0, nessuna deformazione o distorsione è causata dalla deformazione trasversale.

Per ν_xy = -5.44, viene mostrata una rottura post-critica all'estremità libera della piastra e le reazioni del vincolo diventano negative. Il momento massimo si verifica al centro della piastra con 59,5 kNm/m.

La piastra ora si comporta più di una piastra sollecitata uniassiale, senza il terzo vincolo in direzione longitudinale.

Questo comportamento può essere spiegato con la Figura 01 e la relazione qui elencata.

A causa dell'elevata deformazione trasversale negativa (ν_xy = -5.44), la piastra è completamente sovrapressata sul bordo libero e quindi non può essere deformata.

L'influenza dell'ortotropia nella direzione y è quasi nulla qui (E_y ≈ 0).

Conclusione

Quasi tutti i parametri dei materiali possono essere definiti con il modello di materiale ortotropo in RFEM. Risultati molto diversi sono possibili con la variazione delle deformazioni trasversali. Una deformazione trasversale dopo la modifica dei valori secondo [1] risulta in valori che si trovano vicini alla soluzione per una trave a campata singola.

Equazione 31:

M_{y} = \frac{q l^{2}}{8} = 40 kNm

Formula 36

Deformazioni trasversali negative eccessivamente elevate mostrano un sistema strutturale modificato che non corrisponde più alla modellazione.

Autore

Il signor Kuhn è responsabile dello sviluppo di prodotti per strutture in legno e fornisce supporto tecnico ai nostri clienti.

Link

Software per l'analisi non lineare

Bibliografia

Huber, M. T : The Theory of Crosswise Reinforced Ferroconcrete Slabs and Its Application to Various Important Constructional Problems Involving Rectangular Slabs, Der Bauingenieur 12, Seiten 354 - 360, und 13, Seiten 392 - 395. 1923

Download

Hai delle domande?

Eventi

2024-05-16

Considerazione delle fasi costruttive in RFEM 6

Webinar

Considerazione delle fasi costruttive in RFEM 6

2024-05-21

CSA O86:19 Verifica di edifici XLAM in RFEM 6

Webinar

CSA O86:19 Progettazione di edifici XLAM in RFEM 6 (USA)

2024-05-23

Domande frequenti e risposte del supporto tecnico di Dlubal Software

Webinar

Domande frequenti e risposte del supporto tecnico di Dlubal Software | Maggio 2024

2024-08-01

Webinar

Le risposte alle domande FAQ poste al team di supporto di Dlubal | Luglio 2024

2024-10-09 - 2024-10-12

Fiera

SAIE 2024

2024-10-16

Corso di formazione online

RFEM 6 | Studenti | Introduzione alla verifica delle aste

2024-10-23

Corso di formazione online

RSECTION 1 | Studenti | Introduzione alla resistenza dei materiali

2024-10-30

Corso di formazione online

RFEM 6 | Studenti | Introduzione alla FEA

2024-11-05 - 2024-11-07

Conferenza

Vertice dell'ingegneria strutturale NCSEA

2024-11-06

Corso di formazione online

RFEM 6 | Studenti | Introduzione alla verifica acciaio

2024-11-13

Corso di formazione online

RFEM 6 | Studenti | Introduzione alla verifica del calcestruzzo armato

2024-11-20

Corso di formazione online

RFEM 6 | Studenti | Introduzione alla verifica delle strutture di legno

Video

FAQ

FAQ 005037 | I modelli e le presentazioni dell'Info Day 2018 sono disponibili gratuitamente e, posso ...

Durata: 00:00:06 min

Knowledge Base

KB 000863 | Definizione di fallimento del supporto

Durata: 00:00:42 min

Knowledge Base

KB 00693 | Tipo di asta "Molla"

Durata: 00:00:27 min

Knowledge Base

KB 000861 | Disattivazione degli effetti non lineari

Durata: 00:00:14 min

Knowledge Base

KB 000670 | Salvataggio e importazione di diagrammi per vincoli interni delle aste

Durata: 00:00:34 min

Knowledge Base

KB 000583 | Creazione di un modello di materiale elastico-plastico 2D/3D

Durata: 00:00:42 min

Knowledge Base

KB 000601 | Utilizzo del modello di materiale elastico non lineare

Durata: 00:00:40 min

Knowledge Base

KB 000968 | Leggi di snervamento nel modello di materiale elastico non lineare isotropo

Durata: 00:00:43 min

FAQ

FAQ 004898 | Quando definisco il mio materiale, ricevo l'avviso nr. 1136 e non posso continuare a lavorare ...

Durata: 00:00:39 min

Playlist

Modelli da scaricare

3373x

249x

Base di una colonna circolare in acciaio

Modello 004588 | Piastra di ancoraggio della colonna di legno

667x

52x

Piastra di ancoraggio della colonna di legno

291x

12x

Supporto in neoprene

Modello 004572 | Collegamento acciaio-legno

362x

13x

Collegamento acciaio-legno

Modello 004570 | Base in metallo incernierata

269x

15x

Base in metallo incernierata

Modello 004568 | Giunto di travi in legno

321x

14x

Giunto per travi di legno

Modello 004565 | Collegamento di profili HSS tondi

199x

Collegamento a profilo tondo HSS

469x

Esempio di verifica NAFEMS NL07 | 1

422x

Esempio di verifica NAFEMS NL07 | 2

Articoli tecnici della Knowledge Base

Nichtlineares Auflager "Ausfall alle, falls PZ' negativ"

Auflager, die nur bei Druck oder nur bei Zug zum Lastabtrag beitragen, sind in RFEM und RSTAB als nichtlineare Auflager definierbar. Dabei fällt es dem Anwender nicht immer leicht, die richtige Nichtlinearität für "Ausfall bei Zug" oder "Ausfall bei Druck" auszuwählen.

Leggi di più

Das Programm RFEM5 bzw. RSTAB8 bietet bei der Definition eines Stabes unter den Stabtypen eine "Feder" Option an.

Leggi di più

Deaktivierung von nichtlinearen Effekten

Se nel modello vengono utilizzati effetti non lineari, come vincoli esterni, fondazioni, non-linearità delle aste o solidi di contatto, è possibile disattivarli nei parametri di calcolo globali.

Leggi di più

Salvataggio e importazione di diagrammi per i vincoli interni delle aste

In RFEM 5 und RSTAB 8 können Stabendgelenken Nichtlinearitäten zugeordnet werden. Es steht hierbei neben den Nichtlinearitäten "Fest, falls..." und "Teilweise Wirkung..." auch "Diagramm..." zur Verfügung. Wählt man die Option "Diagramm...", sind im zugehörigen Dialog die entsprechenden Einstellungen für die Wirkung des Stabendgelenks einzutragen. Hierbei sind für die einzelnen Definitionspunkte die Abszissen- und Ordinatenwerte (Verformungen beziehungsweise Verdrehungen und zugehörige Schnittgrößen) einzutragen, welche das Gelenk definieren.

Leggi di più

Screenshot

deformazione trasversale

tensioni tangenziali

Sistema

Superfici con rigidezze

Risultati materiale isotropo

Deformazioni e reazioni vincolari di placche ortotropiche

Biegemomente der orthotropen Platte mx (links) und my (rechts)

Ergebnisse der Variation gemäß Tabelle (links: νxy = 5,44, Centro: νxy = 0, a destra: νxy = -5,44)

Modello 004812 | Esempio di verifica 0213 | 1

Caratteristiche del prodotto

È possibile specificare le non linearità degli svincoli delle estremità delle aste (snervamento, strappo, scorrimento, ecc.) e dei vincoli esterni (compreso l'attrito). Sono disponibili finestre di dialogo speciali per determinare le rigidezze delle molle di colonne e pareti in base alle specifiche della geometria.

Leggi di più

Caratteristica 002819 | Grandezze del campo di flusso

In RFEM e RSTAB, è possibile visualizzare i valori del campo di flusso di pressione, velocità, energia cinetica di turbolenza e tasso di dissipazione della turbolenza per la simulazione del vento.

I piani di taglio sono allineati con la rispettiva direzione del vento.

Leggi di più

Caratteristica 002820 | Deformazione plastica limite per le saldature

Nella configurazione ultima per la verifica del giunto acciaio, si ha la possibilità di modificare la deformazione plastica ultima per le saldature.

Leggi di più

Funzione 002821 | Componente "Piastra di base"

Utilizzando il componente "Piastra di base", è possibile progettare collegamenti della piastra di base con ancoraggi gettati in opera. Oltre alle piastre e alle saldature, il progetto analizza l'ancoraggio e l'interazione acciaio-calcestruzzo.

Leggi di più

Domande frequenti (FAQ)

I modelli e le presentazioni dell'Info Day 2018 sono disponibili gratuitamente e potete inviarmeli?

Come funziona il modello di materiale "plastica ortotropa" in RFEM?

Esistono due diversi moduli aggiuntivi per l'analisi dello spettro di risposta in RF‑/DYNAM Pro. Quali possono essere le ragioni dei diversi risultati di entrambi i moduli aggiuntivi?

Durante la conversione dalla definizione manuale delle aree dell'armatura alla disposizione automatica dell'armatura secondo la finestra 1.4, il risultato del calcolo della deformazione differisce, sebbene l'armatura di base non sia stata modificata. Qual è il motivo di questo cambiamento?

Vorrei definire un vincolo esterno della linea con trazione inefficace e applicare la forza di trazione su questa linea utilizzando invece un vincolo esterno nodale. Perché il vincolo esterno della linea continua a ricevere una forza di trazione?

Come è possibile fare combinazioni fattorizzate di un carico permanente nel contesto di form‑finding?

Progetti clienti

Vista esterna dell'unità di produzione e stoccaggio di pasticceria | © GH HERVOUET

Stabilimento di produzione e stoccaggio per pasticceria, Francia

Ponte pedonale e ciclabile "Herzogsteg" a Eichsstutt, Germania

Stazione di pedaggio illuminata | © Sig. Yunchao Ding, Jiangsu Jingong Space Structure Co., Ltd.

Stazione di pedaggio Dawall, in Shaanxi, Cina

Modello RFEM del magazzino a scaffalature alte con i risultati degli spostamenti generalizzati

Grandi scaffalature industriali, Cina

Stazione multi-energy a Les Sables-d'Olonne, Francia

Vista frontale dell'edificio per uffici con le colonne composte in acciaio a forma di V | © Tragwerker GmbH

Edificio per uffici con centro visitatori integrato e garage a Geiselbulach, Germania

Modello di palestra | © BET Moselle Bois

Gymnase de Metz come modello per l'ingegneria e la sostenibilità nell'edilizia moderna, Metz, Francia

Pergola in metallo presso l'Università Rafael Landívar (© Ing. Enrique de León)

Pergola in acciaio in Plaza del Edificio L, Università Rafael Landívar, Guatemala

Torre radar a sinistra (© SAQQARA Ingeniería)

Analisi strutturale della torre radar all'aeroporto di Malaga, Spagna

Prodotti consigliati per te

RFEM 6 | Programma principale RFEM 6

RFEM 6

Programma principale

La nuova generazione del software 3D agli elementi finiti viene utilizzata per l'analisi strutturale di aste, superfici e solidi.

Prezzo della prima licenza 4.170,00 USD

RFEM 6 | Analisi aggiuntive

Comportamento non-lineare del materiale per RFEM 6

Add-on

L'add-on Comportamento non lineare del materiale consente di considerare le non linearità dei materiali in RFEM, ad esempio plastica isotropa, plastica ortotropa, danno isotropo).

Prezzo della prima licenza 1.480,00 USD

RFEM 6 | Analisi aggiuntive

Analisi delle fasi costruttive (CSA) per RFEM 6

Add-on

L'add-on Analisi delle fasi costruttive (CSA) consente di considerare il processo di costruzione di strutture (aste, superfici e strutture solide) in RFEM.

Prezzo della prima licenza 1.570,00 USD

RFEM 6 | Analisi aggiuntive

Analisi time-dependent (TDA) per RFEM 6

Add-on

L'add-on Analisi time-dependent (TDA) consente di considerare il comportamento delle aste in base al tempo. Gli effetti a lungo termine, come viscosità, ritiro e invecchiamento, possono influenzare la distribuzione delle forze interne, a seconda della struttura.

Prezzo della prima licenza 1.030,00 USD

RFEM 6 | Verifica

Analisi tensioni-deformazioni per RFEM 6

Add-on

L'add-on Analisi tensioni-deformazioni esegue l'analisi delle tensioni generali calcolando le tensioni esistenti e confrontandole con le tensioni limite.

Prezzo della prima licenza 1.210,00 USD

RFEM 6 | Verifica

Verifica calcestruzzo per RFEM 6

Add-on

L'add-on Verifica calcestruzzo consente varie verifiche secondo le norme internazionali. È possibile verificare aste, superfici e pilastri ed eseguire verifiche a taglio-punzonamento e deformabilità.

Prezzo della prima licenza 2.550,00 USD

RFEM 6 | Verifica

Verifica acciaio per RFEM 6

Add-on

L'add-on Verifica acciaio esegue le verifiche allo stato limite ultimo e di esercizio delle aste in acciaio secondo varie norme.

Prezzo della prima licenza 2.550,00 USD

RFEM 6 | Verifica

Verifica muratura per RFEM 6

Add-on

L'add-on di RFEM Verifica muratura consente di progettare strutture in muratura utilizzando il metodo degli elementi finiti. È stato sviluppato nell'ambito del progetto di ricerca intitolato DDMaS - Digitalizzazione della verifica di strutture in muratura. Il modello del materiale rappresenta il comportamento non lineare della combinazione mattone-malta sotto forma di macro modellazione.

Prezzo della prima licenza 1.660,00 USD