Всю тему можно легко проиллюстрировать на примере однопролетной балки. Hierzu werden nachfolgend drei Systeme beschrieben. Diese Modelle sind in der Datei im Anhang dokumentiert.
System 1
Statisch bestimmtes System (keine Bettung), dT = 80 ° auf der Oberseite
Der Stab krümmt sich nach oben, ist aber an sich spannungsfrei.
System 2a
Wie System 1, allerdings mit einer zusätzlichen Stabbettung. Die Stabbettung ist hierbei ohne möglichen Ausfall (Nichtlinearität) eingegeben.
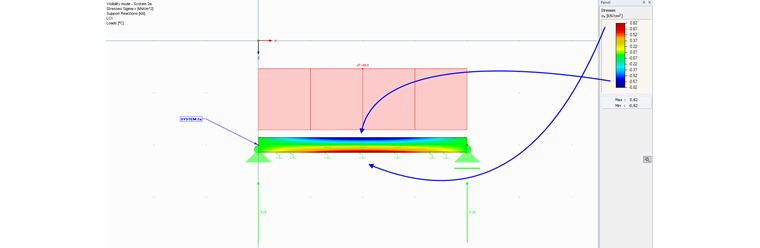
Wenn man sich für das System 2a die Spannungen sigma_x des Stabes darstellen lässt, erhält man auf der Staboberseite Druck und auf der Stabunterseite Zug (siehe Bild 01).
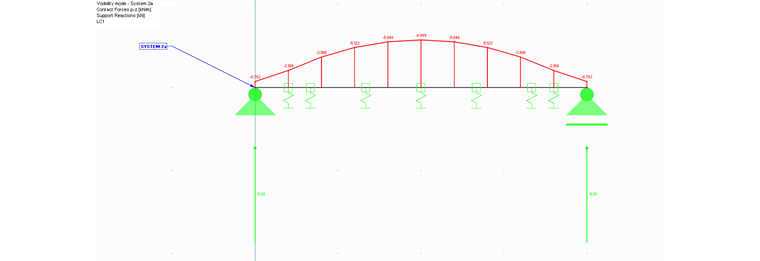
Durch die Krümmung des Stabes und die vorhandene Stabbettung wird eine Kontaktkraft p-z hervorgerufen, welche die Krümmung des Stabes nach oben behindern soll (siehe Bild 02).
Diese Kontaktkräfte p-z (Bild 02) werden durch die Krümmung des Stabes aufgrund der Temperatur und der angesetzten Stabbettung verursacht. Die dargestellten Kontaktkräfte können durch eine der Krümmung entgegengesetzte Stablast ersetzt werden. Dies ist im System 2b in der Beispieldatei dargestellt.
System 2b
Die Stabbettung wird entfernt und die veränderliche Stablast in Z-Richtung eingegeben.
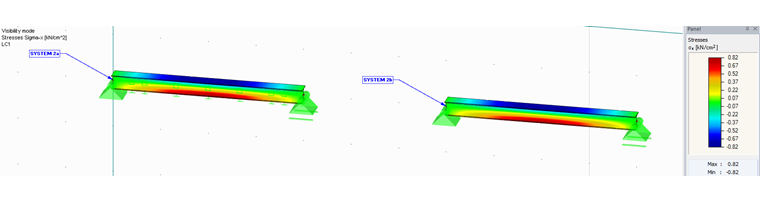
Beim Vergleich der Ergebnisse (z. B. die Verformungen u-z) an den beiden Systemen 2a und 2b erhält man gleichwertige Ergebnisse (siehe Bild 03).
Zusätzlich lassen sich für die beiden Systeme 2a und 2b auch die Spannungen sigma_x darstellen. Diese sind ebenfalls gleichwertig (siehe Bild 04).
System 3
System 3 wurde lediglich zur Dokumentation der Spannungen aufgrund Temperaturdifferenz an einem statisch bestimmten System (ohne Bettung) eingeführt.
Die im Beispiel "Einfeldträger" dokumentierten Ergebnisse lassen sich auch auf elastisch gebettete Flächen übertragen.