Проницаемые или пористые среды используются в CFD для моделирования сложных компонентов, которые не являются полностью твердыми. В реальном мире это, например, проволочные сетки, перфорированные фасады и облицовка, жалюзи, блоки труб (стопки горизонтальных цилиндров) и т. Д. Модели этих структур могут иметь настолько сложную геометрию, что их невозможно эффективно объединить в сетку, создаваемая сетка может быть очень мелкой или, в некоторых случаях, низкого качества. Такие случаи приводят к аппаратным и длительным вычислениям или к неточным вычислениям. Поэтому для таких конструкций предпочтительно использовать модель проницаемых сред.
Исходя из физических соображений, основанных на экспериментальных измерениях, мы предполагаем, что в проницаемой зоне энергия удаляется из потока в виде перепада давления. Мы предполагаем, что с ростом скорости через проницаемую зону перепад давления растет. Падение давления в зоне может быть выражено полиномиальной функцией скорости, где линейная часть - это член вязкости, а квадратичная часть - инерционный член (динамический напор):
Затем мы реализуем эффект проницаемости в уравнениях Навье-Стокса (уравнения НС).
Проницаемость в уравнениях НЗ
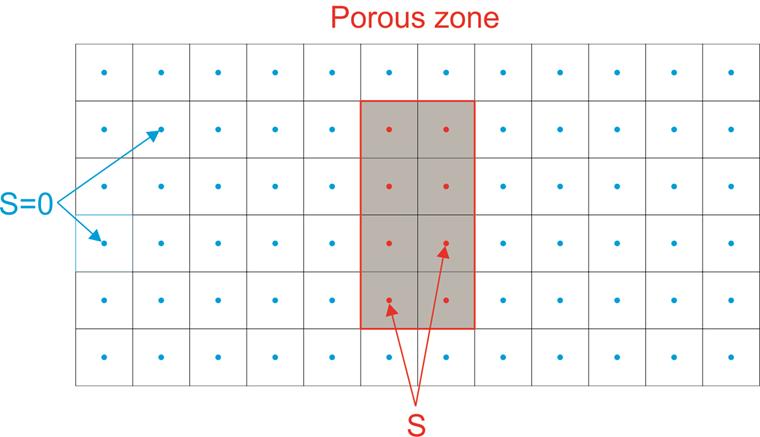
Далее следует краткое введение в численное моделирование проницаемости. Эффект проницаемости добавляется как исходный член в правой части уравнений НС . Важно не включать перепад давления непосредственно в наши уравнения, но исходный член должен быть выражен через перепад давления. Исходный член S применяется к центроидам ячеек проницаемой зоны, член S равен нулю в ячейках, где проницаемая зона не определена, см. Image035160 image ниже.
Исходный член formula001247 - это сила, выраженная падением давления, относящимся к объему ячейки. После некоторых модификаций исходный член для уравнения в направлении потока можно записать в следующей форме:
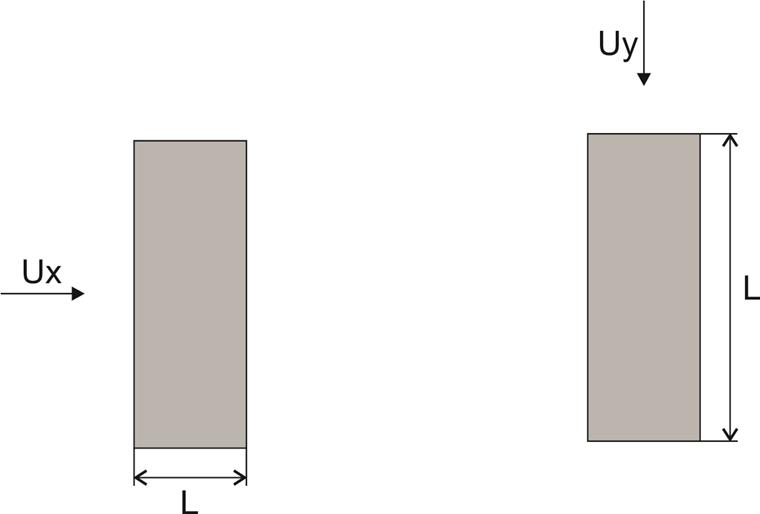
Длина (толщина) проницаемой среды L выражает толщину проницаемой среды в направлении потока image035161 .
Теперь у нас есть исходный член, который описывает потерю давления в проницаемой среде. Далее необходимо указать коэффициенты formula001250 :
Для этого необходимо другое соотношение - закон Дарси. Закон Дарси действует для медленного ламинарного потока через проницаемую среду при малых числах Re. Он задается соотношением:
| α [м2 ] | Проницаемость |
| μ [Па.с] | Динамическая вязкость жидкости |
| Ux[м/с] | Скорость жидкости вдоль x |
Сравнивая это с общим соотношением падения давления, получается уравнение для C1 :
Закон Дарси дает нам соотношение для C1 как функции динамической вязкости, проницаемости и длины проницаемой среды, далее нам нужно указать коэффициент C2. Есть несколько способов сделать это. Либо вы можете использовать эмпирические данные, полученные при измерении перепада давления и скорости или расхода через проницаемую зону. Коэффициент C2 можно подобрать на основе полиномиальной регрессии измеренных данных. Или вы можете использовать некоторые опубликованные данные, например, эмпирические данные для проницаемого диска, сравнить их с геометрией (сравнить количество отверстий и их геометрию) и получить коэффициенты. Некоторые подходы к определению коэффициентов можно найти здесь , этот подход описан в нашем Статья базы знаний.