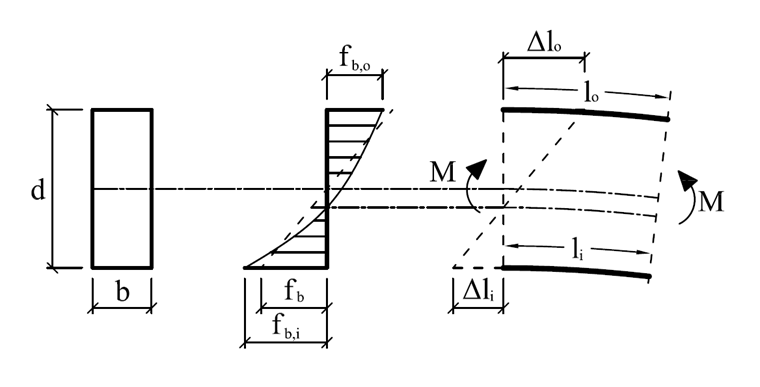
Из-за геометрической формы и процесса изготовления криволинейного дощато-клееного бруса необходимо выполнить специальные проверки во время расчета. С одной стороны, изменение изгибающего напряжения вдоль глубины балки не является линейным; кроме того, напряжения возникают во время изготовления из-за изгиба ламелей. Первое связано с тем, что древесные волокна внутри короче, чем снаружи. Таким образом, справедливо следующее, согласно допущению Бернулли (плоские сечения остаются плоскими) и предполагая, что нулевая линия находится в центре тяжести:
Принимая во внимание закон Гука, внутренние краевые напряжения больше внешних:
fb = E ∙ ε → fb, i > fb, o
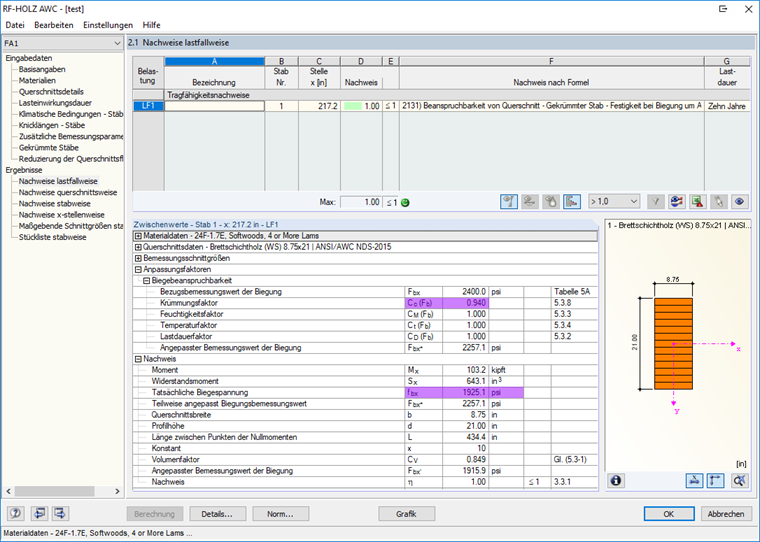
Данные характеристики учитываются в расчете по [1] с помощью коэффициента кривизны Cc , который служит в качестве поправочного коэффициента для расчетного значения прочности на изгиб:
Fb '= Fb ∙ CD ∙ CM ∙ Ct ∙ CV ∙ Cc
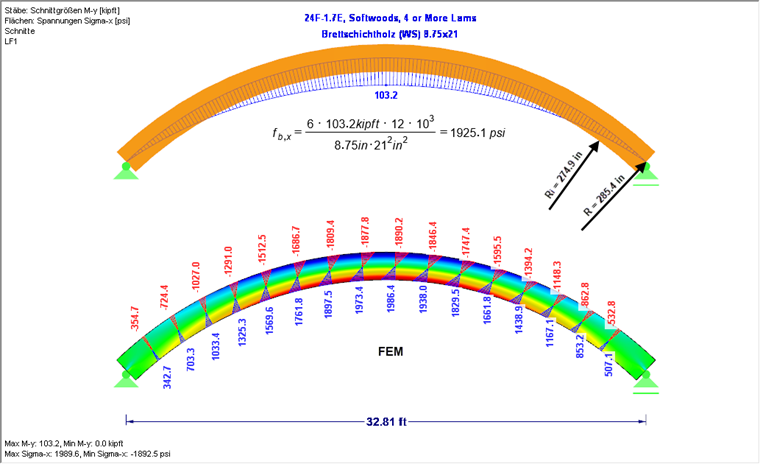
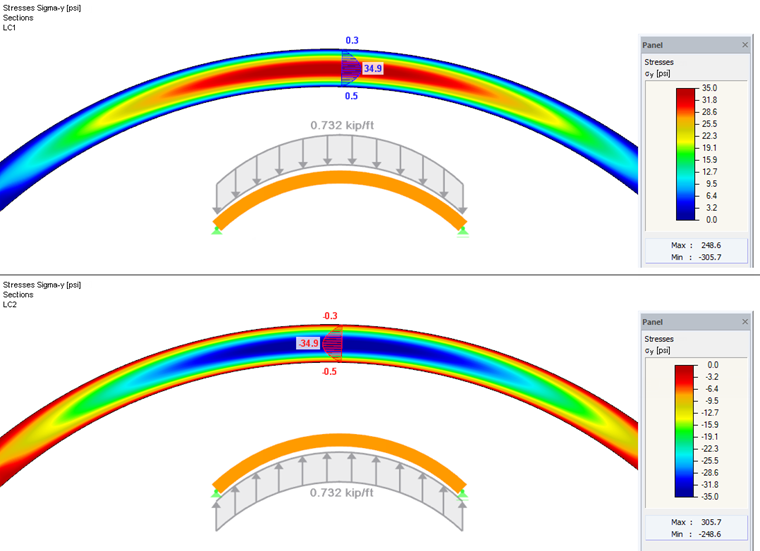
Для системы, показанной на рисунке 03, с учетом 20-кратного собственного веса и линейного распределения напряжений, максимальное изгибающее напряжение в поперечном сечении кромки составляет 1925,1 фунтов на квадратный дюйм. Учитывая напряжения в расчете по МКЭ (см. Рисунок 03 ниже), и как объяснено выше, отображаются большие изгибающие напряжения (1986,4 фунтов на квадратный дюйм), как ожидалось.
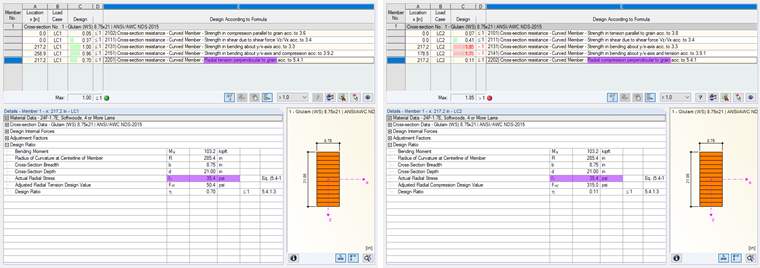
При расчете криволинейных балок в модуле RF-/TIMBER AWCучитывается это несоответствие с коэффициентом кривизны C c , как требуется в [1] (см. Рисунок 04).
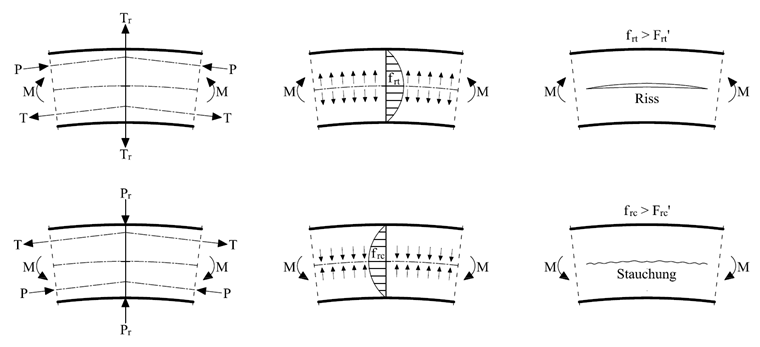
Если изгибающий момент увеличивает радиус кривизны, то дополнительно возникают растягивающие напряжения, поперечные волокнам. Если изгибающий момент уменьшает радиус кривизны, возникают сжимающие напряжения, проходящие через волокно. Схематическое изображение возникновения этих напряжений показано на рисунке 05 с учетом линейного распределения продольных напряжений (fb, x ).
Данные радиальные напряжения должны учитываться при расчете, поскольку они оказывают решающее влияние на несущую способность. В постоянном поперечном сечении по глубине балки они приводят к:
Напряжения становятся максимальными на высоте нейтральной оси, из этого следует:
Поскольку данные радиальные напряжения не могут быть определены с помощью балки (1D), они должны определяться аналитически. На рисунке 06 показаны результаты расчета по МКЭ (2D) для поперечного (вверху) и бокового (внизу). Результаты практически идентичны аналитическому решению, используемому для расчета балок в модуле RF-/TIMBER AWC (см. Рисунок 07).
Если не произвести проверку, древесина будет трескаться на уровне нейтральной оси (см. Рисунок 05 справа). Чтобы предотвратить это, могут быть вкручены поперечные растягивающие связи, например, полнонарезные болты, которые поглощают поперечные растягивающие напряжения. Сила, действующая на болт, может быть приблизительно определена вручную, следующим образом:
Tr,t = frt ∙ b ∙ s = 35.4 psi ∙ 8,75 in. ∙ 11,5 in. = 3,562 lbf
Tr, t = радиальная сила в винте
frt = напряжение при радиальном растяжении
b = ширина балки
s = расстояние между радиальным армированием
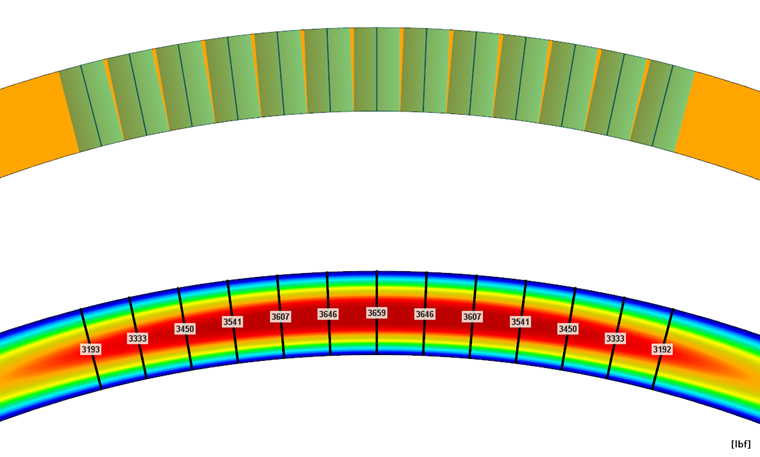
В случае поверхностной модели в RFEM можно перенести данные силы непосредственно из внутренних сил на поверхности на результирующую балку. Результирующая балка не приносит дополнительной жесткости в системе, а только интегрирует внутренние силы на поверхностях. Таким образом, можно прямо считывать нормальное усилие в балке или армирующем элементе (см. Рисунок 08).
В RFEM можно детально рассчитать еще более сложные формы опор. Если форма балки отличается от стандартизованных форм, расчет по МКЭ с поверхностями может быть очень полезен, как описано выше.