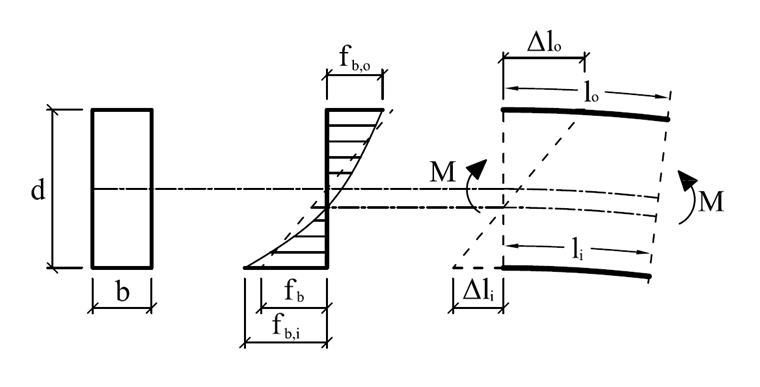
Bedingt durch die geometrische Form und den Herstellungsprozess eines gekrümmten Brettschichtholzes gilt es bei der Bemessung gesonderte Nachweise zu führen. Zum einen ist der Verlauf der Biegespannung entlang der Trägerhöhe nicht linear, des Weiteren entstehen während der Herstellung Spannungen infolge des Biegens der Lamellen. Ersteres ist darauf zurückzuführen, dass die Fasern auf der Innenseite kürzer sind als die an der Außenseite. Somit gilt unter der Voraussetzung der bernoullischen Annahmen (Ebenbleiben der Querschnitte) und der Annahme, dass die Nulllinie sich im Schwerpunkt befindet:
Unter Berücksichtigung des hookeschen Gesetzes sind die inneren Randspannungen größer als die äußeren:
fb = E ∙ ε → fb,i > fb,o
Diese Besonderheiten werden bei der Bemessung nach [1] mit dem Curvature Factor Cc berücksichtigt, welcher als Anpassungsfaktor für den Bemessungswert der Biegefestigkeit dient:
Fb' = Fb ∙ CD ∙ CM ∙ Ct ∙ CV ∙ Cc
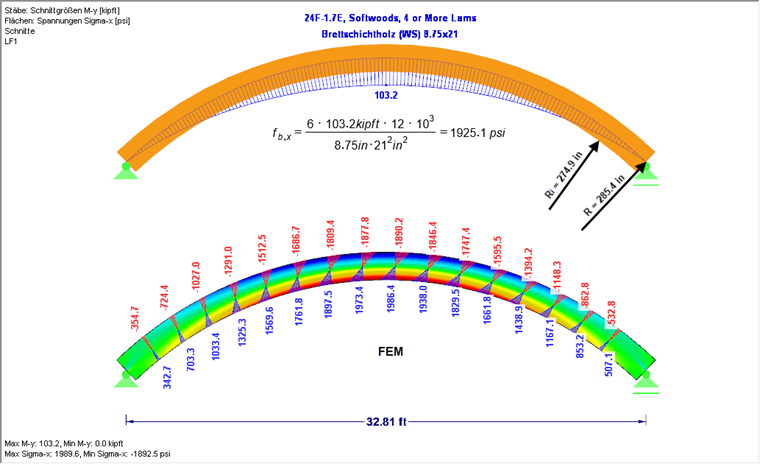
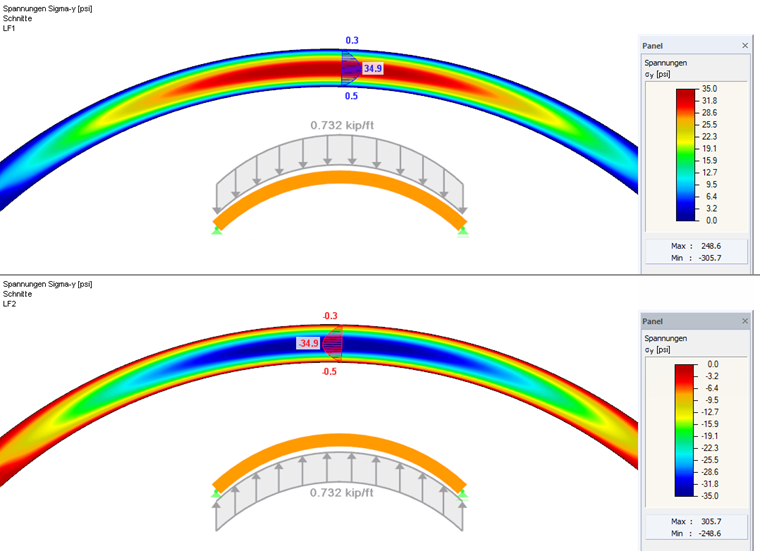
Für das in Bild 03 dargestellte System resultiert unter Berücksichtigung des 20-fachen Eigengewichtes und einer linearen Spannungsverteilung eine maximale Biegespannung im Firstquerschnitt von 1925,1 psi. Betrachtet man die Spannungen in einer FEM-Analyse (siehe Bild 03 unten) werden wegen vorstehender Erläuterung wie erwartet größere Biegespannungen (1986,4 psi) ausgegeben.
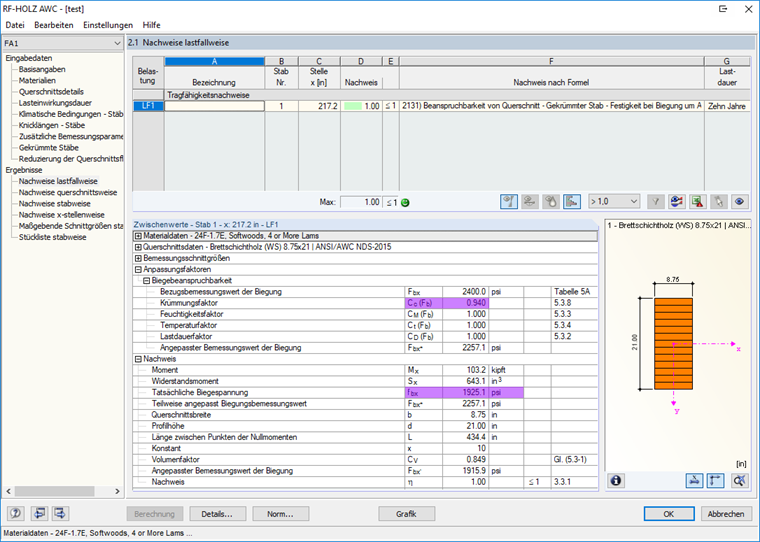
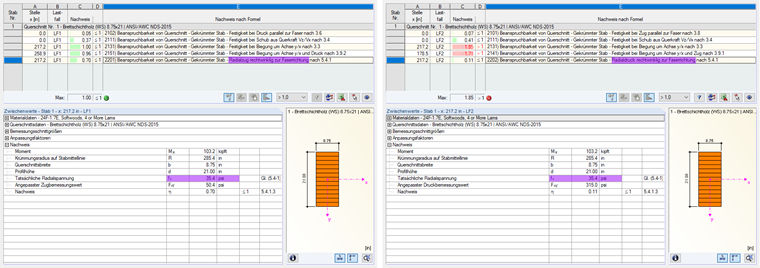
Für die Bemessung des gekrümmten Trägers in RF-/HOLZ AWC wird, wie in [1] gefordert, diese Diskrepanz mit dem Curvature Factor Cc berücksichtigt (siehe Bild 04).
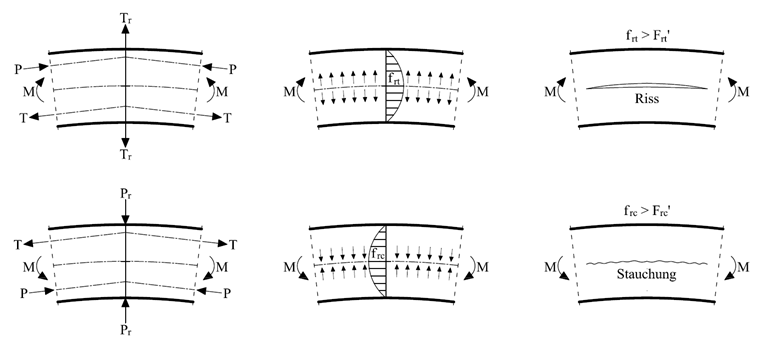
Vergrößert das Biegemoment den Krümmungsradius, entstehen dadurch zusätzlich Zugspannungen quer zur Faser. Verkleinert das Biegemoment den Krümmungsradius, entstehen Druckspannungen quer zur Faser. Eine schematische Darstellung wie diese Spannungen zustande kommen, ist unter Berücksichtigung einer linearen Längsspannungsverteilung (fb,x) in Bild 05 dargestellt.
Diese Radialspannungen müssen bei der Bemessung berücksichtigt werden, da sie die Tragfähigkeit entscheidend beeinflussen. Sie resultieren bei einem konstanten Querschnitt über die Trägerhöhe zu:
Die Spannungen werden auf Höhe der neutralen Achse maximal, woraus folgt:
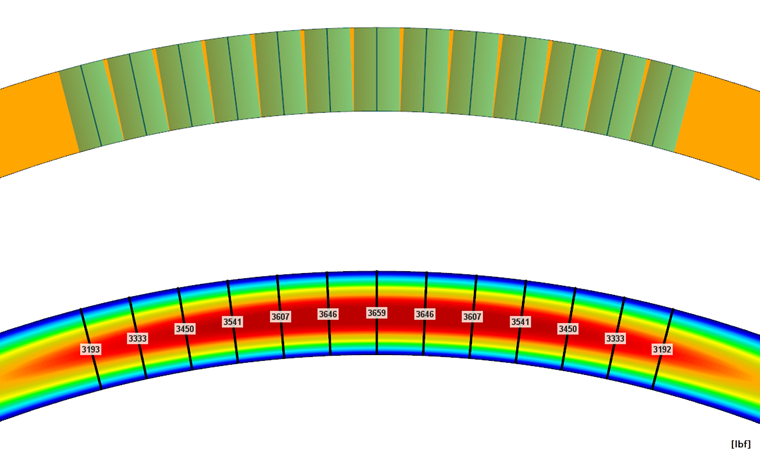
Da diese Radialspannungen bei einem Stab (1D) nicht erfasst werden können, müssen diese analytisch ermittelt werden. In Bild 06 werden die Ergebnisse aus der FEM-Berechnung (2D) für Querzug (oben) und Querdruck (unten) dargestellt. Die Ergebnisse sind nahezu identisch mit der analytischen Lösung, welche für die Stabbemessung in RF-/HOLZ AWC angewendet wird (siehe Bild 07).
Wird der Nachweis nicht erbracht, wird das Holz auf Höhe der neutralen Achse aufreißen (siehe Bild 05 rechts). Um dem vorzubeugen, können Querzugverstärkungen zum Beispiel in Form von Vollgewindeschrauben eingedreht werden, welche die Querzugspannungen aufnehmen. Die auf die Schraube wirkende Kraft kann näherungsweise händisch wie folgt ermittelt werden:
Tr,t = frt ∙ b ∙ s = 35,4 psi ∙ 8,75 in ∙ 11,5 in = 3,562 lbf
Tr,t = radial force in screw
frt = radial tension stress
b = beam width
s = spacing between radial reinforcement
Bei einem Flächenmodell in RFEM hat man die Möglichkeit, diese Kräfte direkt aus den Flächenschnittgrößen auf einen Ergebnisstab aufintegrieren zu lassen. Dieser Ergebnisstab bringt keine weitere Steifigkeit mit in das System, sondern integriert nur die Flächenschnittgrößen. Somit kann die Normalkraft des Stabes beziehungsweise des Verstärkungselementes direkt abgelesen werden (siehe Bild 08).
Mit RFEM können auch komplexere Trägerformen detailliert bemessen werden. Weichen die Trägerformen von den normierten Trägerformen ab, kann wie gezeigt eine FEM-Berechnung mit Flächen hilfreich sein.