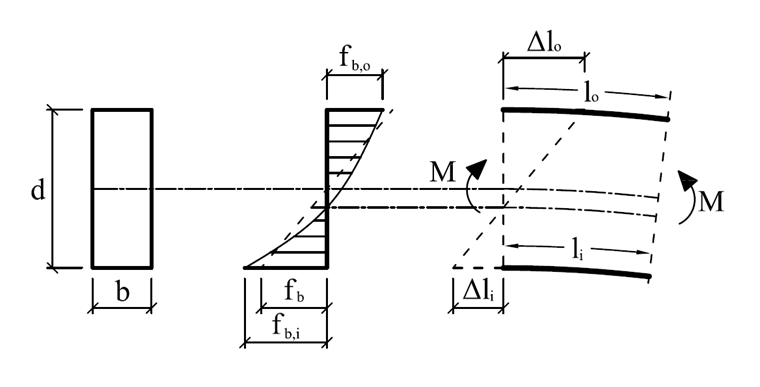
由于弯曲层板胶合木梁几何形式和生产制造过程的原因,需要按照特殊的方法进行其截面设计和验算。 一方面延梁截面高度方向的弯曲正应力为非线性,另一个方面由于在生产制造过程中层压木板之间的弯曲产生的初始应力。 首先需要考虑,构件内侧纤维与外侧纤维相比其长度较短。 因此计算需按照伯努利假设的条件(截面保持平面)并假设截面的应力零线与重心线位置重合:
考虑胡克定律后,内部的边缘应力大于外部的边缘应力:
fb = E∙ε→fb,i > fb,o
在按照[1]进行设计时考虑使用曲率系数Cc进行抗弯抗弯承载力设计值的调整系数的情况,
Fb '= Fb ∙CD ∙CM ∙Ct ∙CV ∙Cc
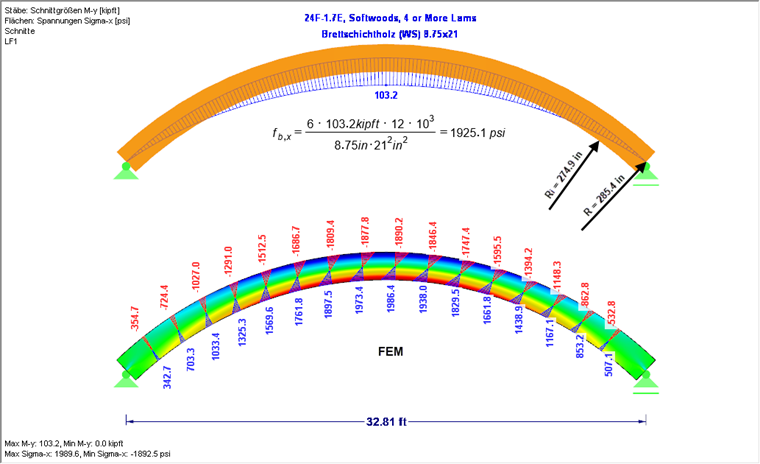
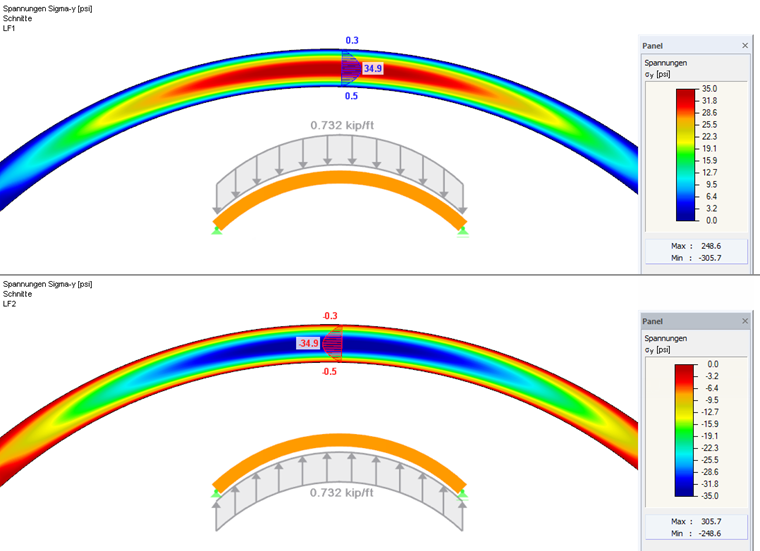
在本例题图 03 所示的结构体系中添加了等效于 20 倍自重的荷载,在弯曲梁截面最高位置其线性应力分布曲线的最大弯曲应力值为 1925,1 psi。 与在有限元 FEM-分析 (图 03 下图)比较,按照上述的设定其最大弯曲应力值为 1986,4 psi。
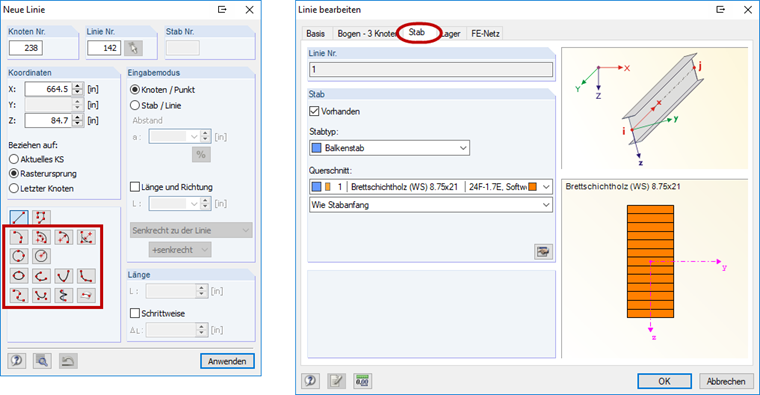
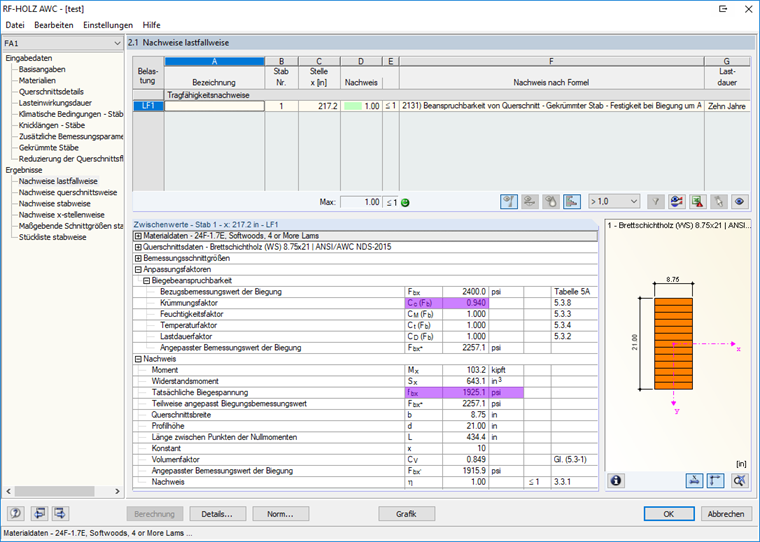
在附加模块RF-/TIMBER AWC中设计弯曲类型梁时可以按照[1]中的规定考虑曲率系数C c引起的差异(见图04)。
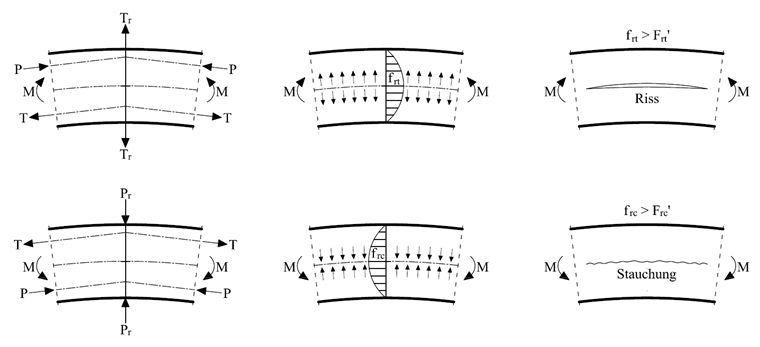
正向弯矩作用下会增大弯曲杆件的曲率半径,由此会产生垂直于纤维方向上的附加拉应力。 负向弯矩作用下会减小弯曲杆件的曲率半径,由此会产生垂直于纤维方向上的附加压应力。 图05中显示了这些应力如何产生,并考虑了纵向的线性应力分布(fb,x )。
由于此项沿半径方向上的应力对构件的承载力影响非常大,所以验算承载力时必须考虑此项。 等截面梁的应力数值沿截面高度方向上的大小可以按照下式计算:
应力在中性轴上的数值达到最大,按照下式计算为:
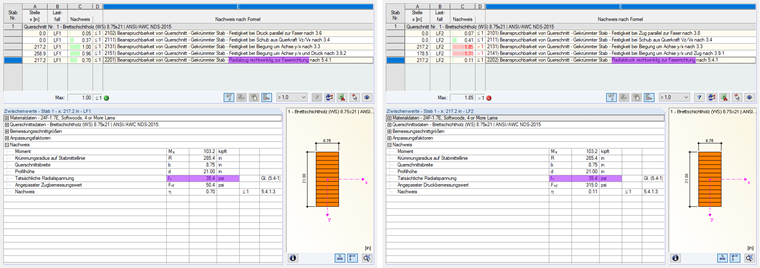
由于此径向应力在一维杆件(1D)中无法计算,必须使用解析分析方法进行计算。 图06显示了横向(上)和外侧(下)的有限元计算(二维)结果。 计算结果与在RF-/TIMBER AWC中计算梁的分析结果几乎相同(见图07)。
如果上述的验算不满足要求,木材将沿着截面中性轴撕裂(见图 05 右侧)。 为避免上述的情况发生,需要在截面设置横向抗拉加强件,例如设置全螺纹螺钉用于承担横向拉应力。 作用于螺栓上的荷载可以按照下列的公式进行手算:
Tr,t = frt ∙ b ∙ s = 35.4 psi ∙ 8.75 in. ∙ 11.5 in. = 3.562 lbf
Tr,t =螺栓径向力
frt =径向拉应力
b = beam width
s = spacing between radial reinforcement
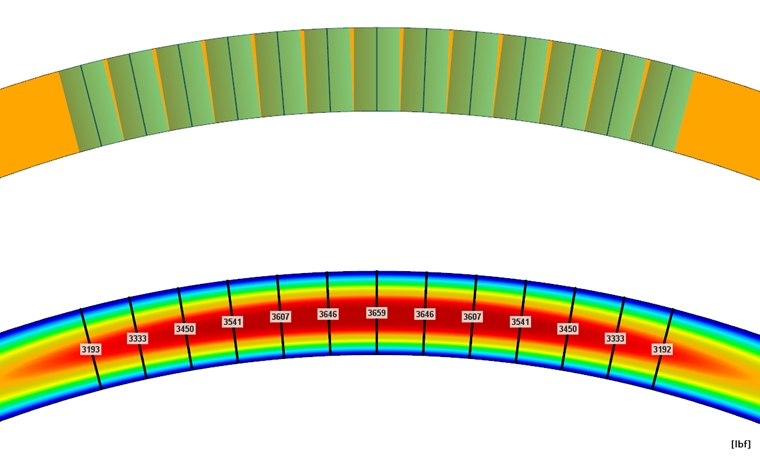
如果在 RFEM 中建立面模型,可以将面的内力值集成到结果杆件上。 结果杆件并不改变结构体系的刚度,其作用仅仅是将面的内力集成到杆件上。 由此则可以将杆件或者加强连接件的轴力直接读取并显示出来(见图形 08)。
由本例可见,使用有限元软件 RFEM 可以计算非常复杂的梁的结构形式。 如前文所述如果梁的形式与一般类型的梁不同,那么可以使用 RFEM 的有限元方法计算面,将会为复杂结构的计算提供极大的帮助。