La forme géométrique et procédure de fabrication de bois lamellé-collé courbe, rendent nécessaire de réaliser des contrôles séparés lors du calcul. Tout d’abord, la contrainte de flexion le long de la profondeur de poutre n’est pas linéaire, ce qui est dû au fait que les grains internes sont plus petits que ceux en externe. Les contraintes apparaissent lors de la fabrication à cause de la flexion des lamelles. Ainsi, si nous supposons la théorie d’Euler-Bernoulli (les sections planes restent planes) et que nous supposons que la ligne nulle est au centre de gravité :
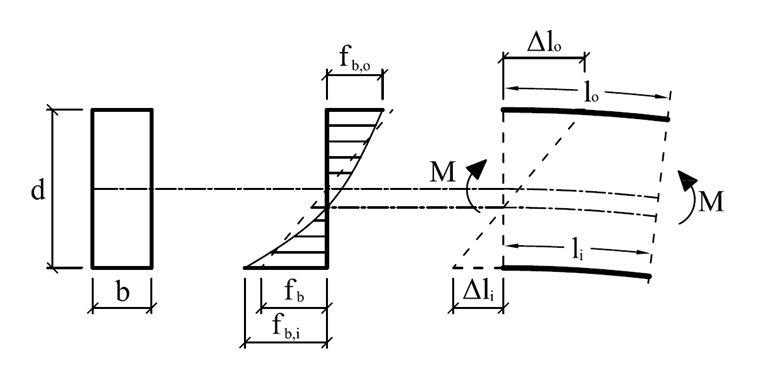
Si nous considérons la loi de Hooke, les contraintes de bord intérieur sont supérieurs à celles du bord extérieur :
fb = E ∙ ε → fb,i > fb,o
Ces caractéristiques sont considérées dans le calcul selon [1] avec le coefficient de courbure Cc, qui sert de coefficient d’ajustement pour la valeur de calcul de la résistance en flexion :
Fb' = Fb ∙ CD ∙ CM ∙ Ct ∙ CV ∙ Cc
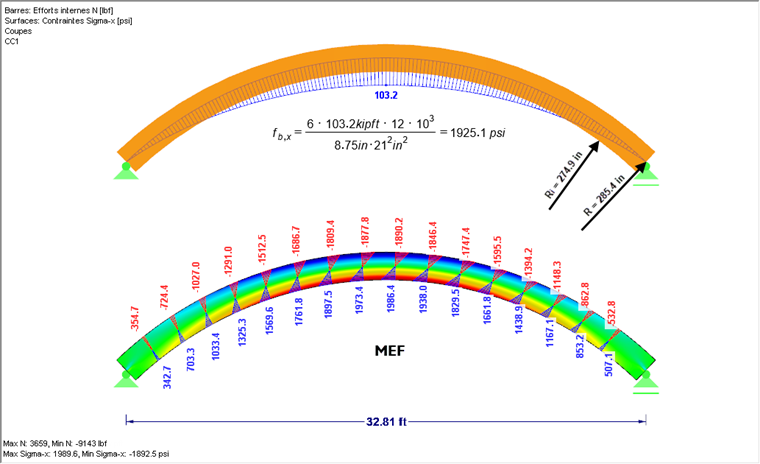
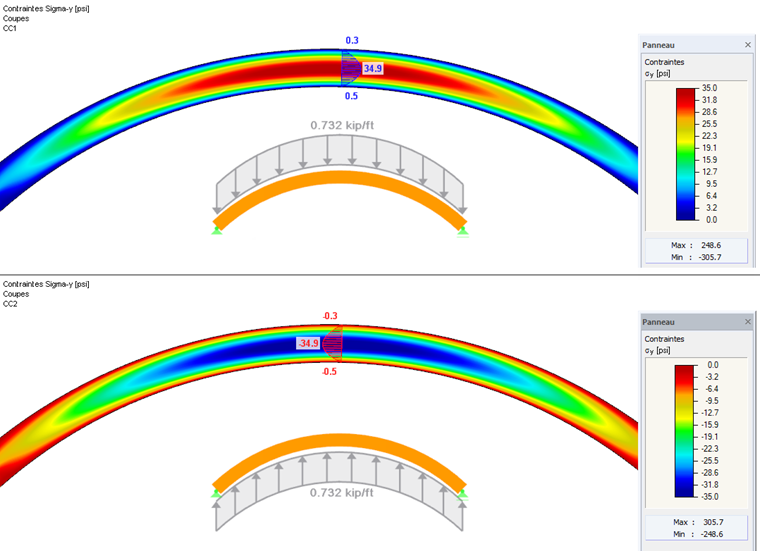
Le système affiché dans la Figure 03, qui considère 20 fois son poids et une répartition linéaire des contraintes, résulte d’une contrainte de flexion maximum dans la section de faîtage, de 1925,1 psi. En considérant les contraintes dans le calcul aux éléments finis (voir la Figure 03 ci-dessous), et comme expliqué auparavant, des contraintes de flexion plus importantes (1986,4 psi) sont, comme prévu, affichées.
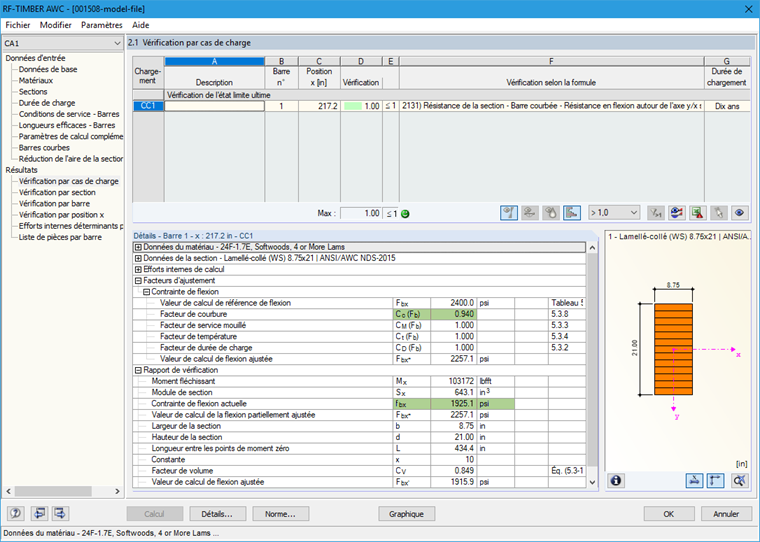
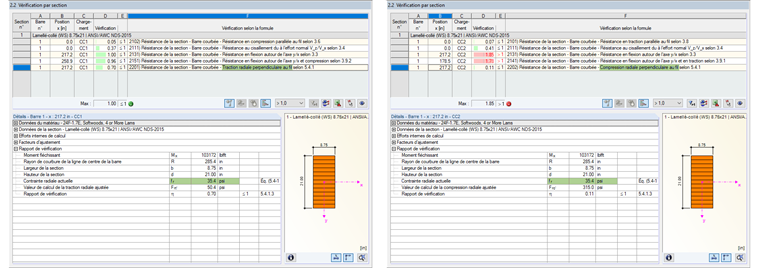
Le calcul de poutres courbes dans RF-/TIMBER AWC requiert que cet écart du Coefficient de courbure Cc soit considéré, conformément à [1] (voir la Figure 04 ).
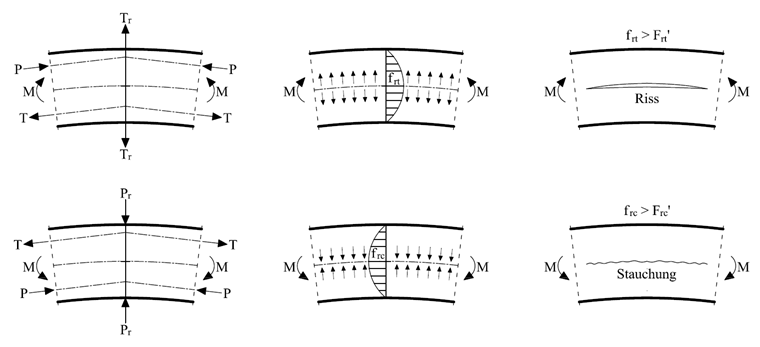
Si le moment fléchissant augmente le rayon de courbure, des contraintes transversales en traction du grain ont lieu. Si le moment fléchissant réduit le rayon de courbure, des contraintes en compression ont lieu dans le grain. Une représentation schématique de l’apparition de ces contraintes est affichée dans la Figure 05, en considérant une répartition longitudinale linéaire des contraintes (fb,x).
Ces contraintes radiales doivent être considérées dans le calcul du fait de leur impact déterminant dans la capacité porteuse. Ils résultent d’une section constante sur la profondeur de poutre :
Les contraintes deviennent maximales au niveau de l’axe neutre, ce qui résulte de :
Ces contraintes radiales ne pouvant pas être détectées avec une poutre (1D), celles-ci doivent être déterminées analytiquement. La Figure 06 montre les résultats du calcul MEF (2D) pour les valeurs transversales (en haut) et latérales (en bas). Les résultats sont presque identiques à ceux de la solution analytique utilisée pour le calcul des poutres dans RF-/TIMBER AWC (voir la Figure 07).
Si l’évaluation n’est pas disponible, le bois sera en rupture au niveau de l’axe neutre (voir la Figure 05). Afin d’éviter ceci, des éléments pour renforcer le bois peuvent être vissés, par exemple sous la forme de vis filetées, qui absorbent les contraintes de traction transversale. La force agissant sur la vis peut être déterminée manuellement de manière approximative, comme suit :
Tr,t = frt ∙ b ∙ s = 35.4 psi ∙ 8.75 in ∙ 11.5 in = 3.562 lbf
Tr,t = force radiale dans la vis
frt = contrainte de traction radiale
b = largeur de poutre
s = espacement entre armatures radiales
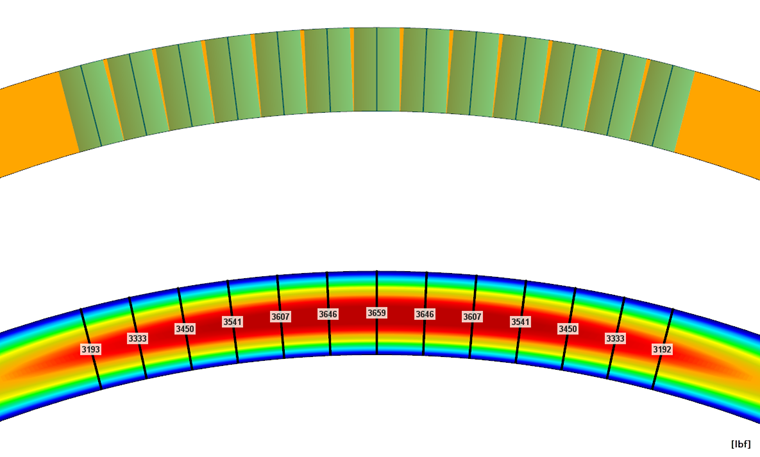
Dans le cas d’un modèle surfacique dans RFEM, il est possible d’intégrer ces forces directement à partir des efforts internes des surfaces en poutre résultante. Cette poutre résultante n’apporte pas de rigidité supplémentaire dans le système, ne fait qu’intégrer les efforts internes dans les surfaces. Ainsi, l’effort normal de la poutre ou de l’élément de renfort peut être directement lu (voir la Figure 08).
Avec RFEM, même des formes complexes d’appui peuvent être calculées en détail. Si les formes des poutres dévient des formes standard des poutres, un calcul aux éléments finis avec surfaces, comme expliqué dans cet article, peut être utile.