Они возникают в результате запланированного внецентренного приложения нагрузки, несовершенств конструкции (геометрические и материальные несовершенства), а также дополнительного эксцентриситета из расчета по методу второго порядка.
Запланированные эксцентриситеты
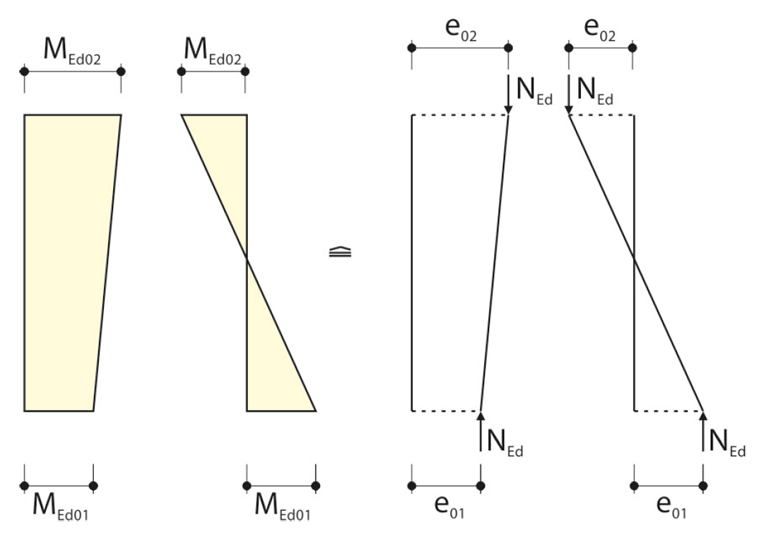
Эксцентриситеты от запланированного внецентренного действия нагрузки можно легко определить с помощью моментов от внецентренного приложения нагрузки. Для постоянного распределения момента применяется следующее соотношение:
В этом случае минимальный эксцентриситет по 6.1.(4) равен
где h - высота сечения.Для линейно переменного распределения момента, можно определить эквивалентный эксцентриситет и применить следующую формулу:
Эксцентриситеты необходимо применять с алгебраическими знаками. Они имеют одинаковый знак, если соответствующие моменты создают растяжение на одной и той же стороне.
При наличии распределения моментов, для расчета всегда используется максимальный эксцентриситет, поэтому нет необходимости исключать из расчета колонны.
Непреднамеренные эксцентриситеты из-за несовершенств
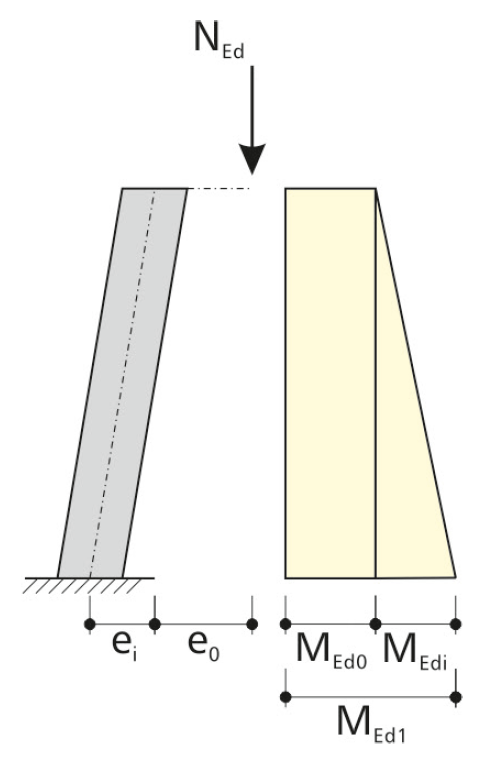
При расчете моментов по методу первого порядка необходимо учесть также геометрические несовершенства и несовершенства материала. Это можно сделать путем применения эквивалентных геометрических несовершенств, которые выражены через отклонение от вертикали на угол θi.
Эксцентриситет определяется в норме EN 1992-1-1 по формуле (5.2):
Отклонение θi рассчитывается по формуле (5.1):
При этом:
Базовое значение несовершенства отклонения
Понижающий коэффициент для высоты
Понижающий коэффициент для количества конструктивных элементов (m - количество колонн)
Изгибающий момент для определения эквивалентного несовершенства ei равен:
Дополнительный эксцентриситет от расчета по методу второго порядка
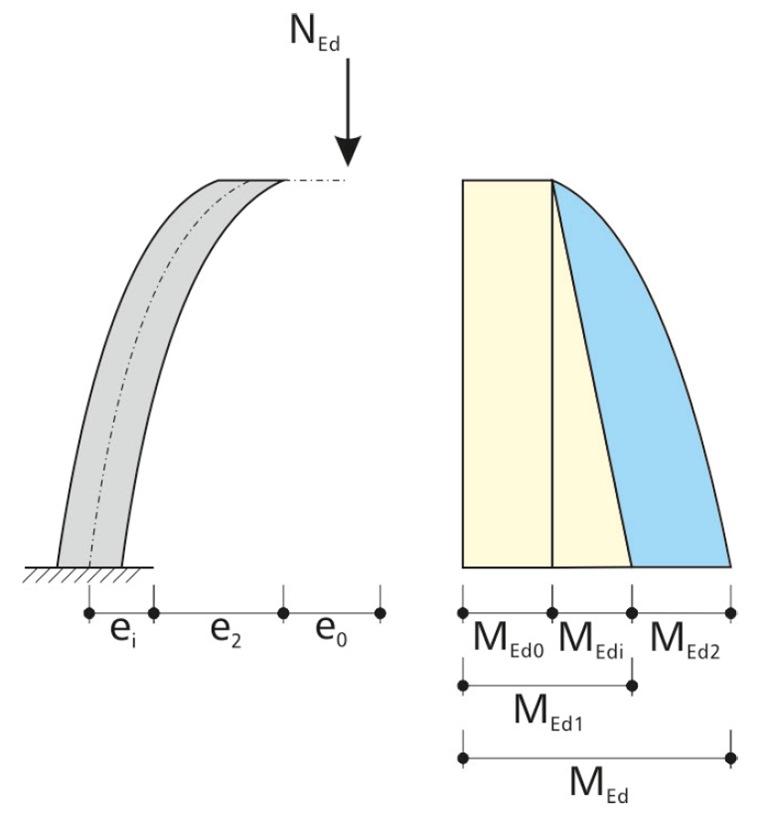
В результате действия нагрузки от нормальной силы возникает кривизна колонны, при которой капитель колонны отклоняется по директории e2. В результате получается распределение моментов по методу второго порядка.
Для метода, основанного на номинальной кривизне, предполагается параболическое распределение момента. Определение эксцентриситета по теории второго порядка выполняется согласно EN 1992-1-1, 5.8.8.2 (3).
Подробную информацию о модуле (RF-)CONCRETE Columns можно найти в нормативе или в руководстве пользователя модуля (RF-)CONCRETE Columns.
Особенности определения эксцентриситетов у эксцентриситета двухосной нагрузки
Для колонн, нагруженных эксцентриситетом двухосной нагрузки, необходимо сначала выполнить отдельный расчет в обеих ориентациях главных осей. В данном расчете несовершенства должны применяться исключительно в том направлении, где они приводят к наиболее неблагоприятным эффектам. Затем расчеты можно выполнить в обоих направлениях со всей примененной арматурой. Таким образом, можно исключить то, что несовершенства требуют двухосного расчета.
Для того, чтобы можно было выполнить расчеты в обоих направлениях без необходимости учета дальнейшего двухосного изгиба, должны быть выполнены условия по уравнению (5.38).
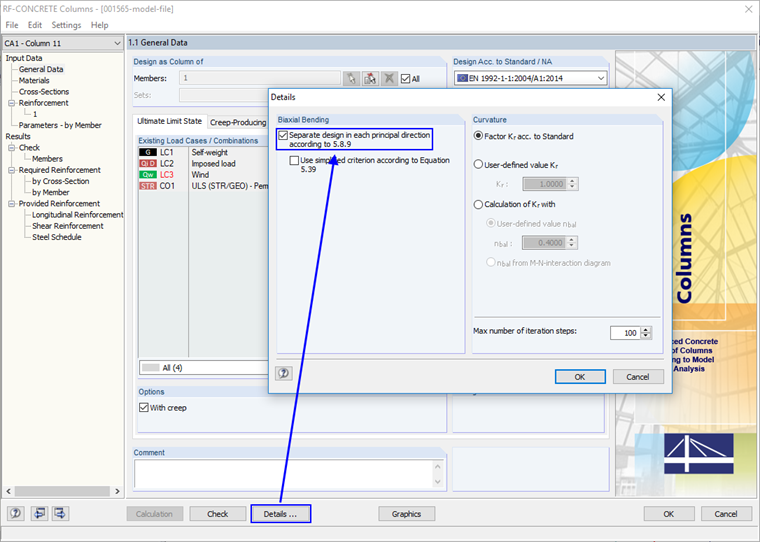
Однако, чтобы выполнить отдельный расчет, необходимо сначала активировать соответствующую функцию в модуле (RF-)CONCRETE Columns.
С одной стороны, необходимо учесть соотношение гибкости в уравнении (5.38a):
Кроме того, должно быть выполнено одно из условий в отношении соответствующих эксцентриситетов нагрузки по уравнению (5.38a):
где
iy и iz - радиусы вращения относительно оси у и оси z.
- эксцентриситеты нагрузки в направлении осей.
При вычислении расчетных моментов MEdy и MEdz не учитывается несовершенство во второстепенном направлении.
Вспомогательное направление определяется через отношение общего эксцентриситета к эксцентриситету по линейному статическому расчету.
для вычисления (5.38b).
В противном случае ei,z будет задано равным 0.
Если при этом выполняется одно из условий уравнения (5.38b), то расчет можно выполнить отдельно, пренебрегая несовершенствами во второстепенном направлении. Если (5.38b) не выполнено, то необходимо выполнить двухосный расчет с учетом всех несовершенств.
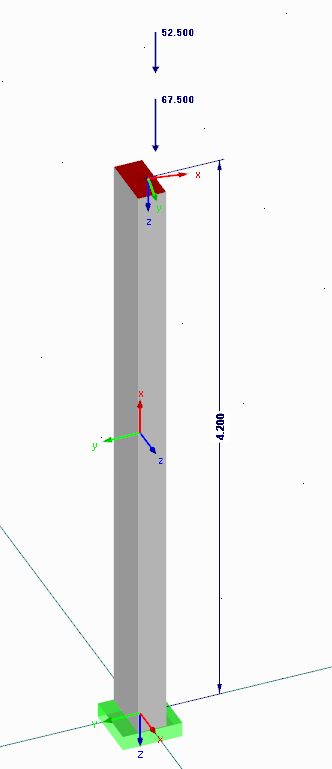
Пример кронштейна
Эксцентриситеты по теории второго порядка импортируются из программы:
e2,y = 238 мм
e2,z = 119,5 мм
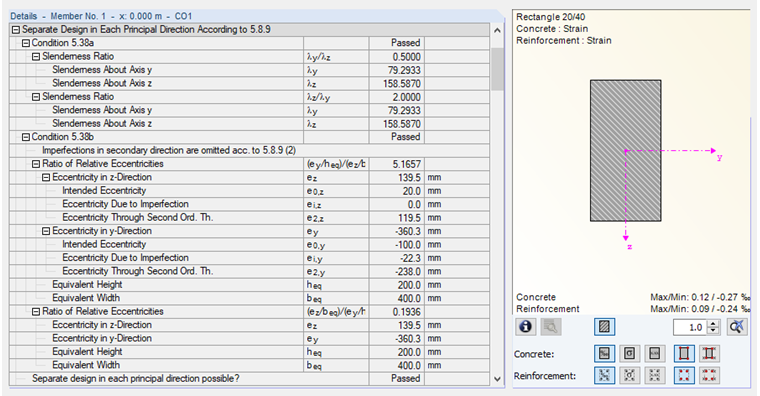
С помощью этих значений можно определить, какое направление является второстепенным.
Таким образом ei,z можно установить на 0, мы получим значения, указанные на рисунке 06.