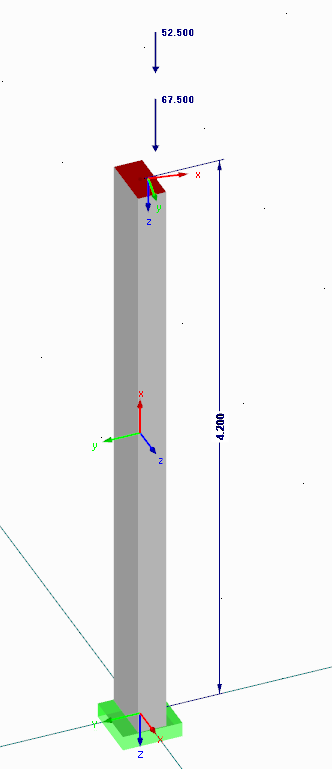
Diese resultieren aus planmäßiger exzentrischer Lasteinleitung, imperfekten Strukturen (geometrische und materielle Imperfektionen) und einer zusätzlichen Exzentrizität aus der Berechnung nach Theorie II. Ordnung.
Planmäßige Exzentrizitäten
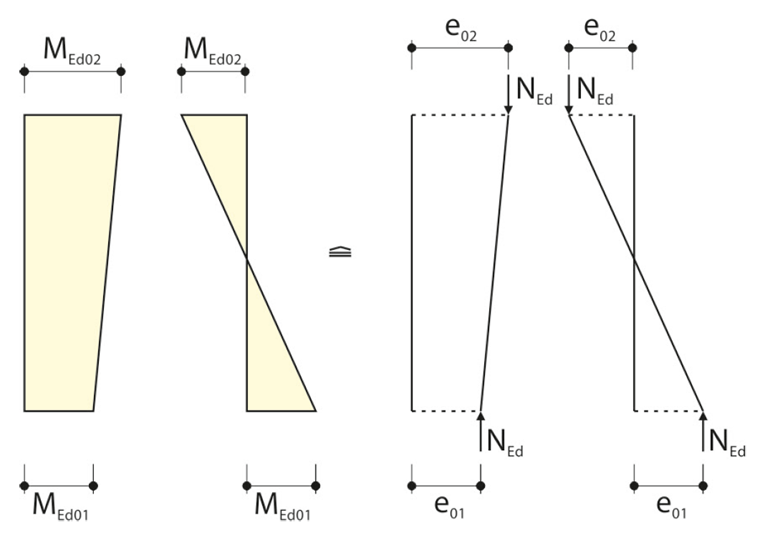
Die Exzentrizitäten aus planmäßiger außermittiger Lasteinleitung lassen sich leicht über die Momente infolge eines exzentrischen Lastangriffs ermitteln. Für einen konstanten Momentenverlauf gilt die Beziehung:
Dabei ist die Mindestausmitte nach Abs. 6.1.(4)
mit h = Querschnittshöhe.Bei einem linear veränderlichen Momentenverlauf darf eine Ersatzausmitte ermittelt und folgende Formel angesetzt werden:
Die Exzentrizitäten müssen dabei mit Vorzeichen angesetzt werden. Sie haben dasselbe Vorzeichen, wenn die zugehörigen Momente auf derselben Seite Zug erzeugen.
Liegt ein beliebiger Momentenverlauf vor, so wird stets mit der maximalen Ausmitte gerechnet, sodass keine Stützen von der Bemessung ausgenommen werden müssen.
Ungewollte Ausmitten durch Imperfektionen
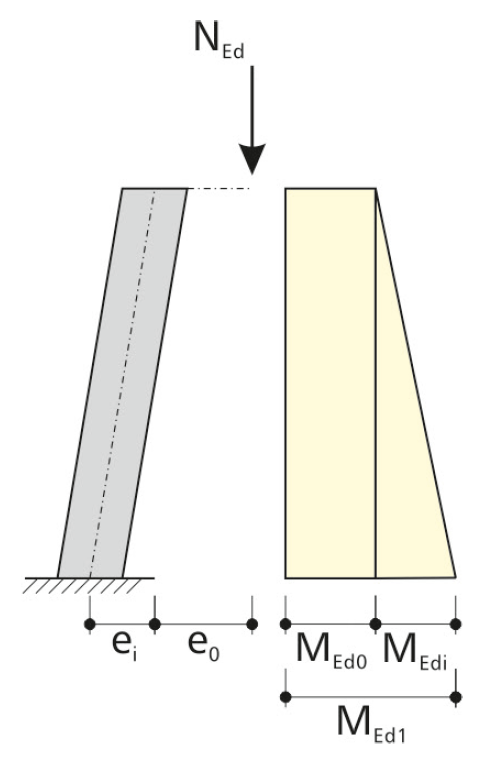
Für die Berechnung der Momente nach Theorie I. Ordnung müssen auch die geometrischen und materiellen Imperfektionen berücksichtigt werden. Dies darf durch den Ansatz geometrischer Ersatzimperfektionen geschehen, welche als Schiefstellung θi erfasst werden.
Die Ausmitte wird in EN 1992-1-1 nach Formel (5.2) ermittelt:
Die Schiefstellung θi wird dabei nach Formel (5.1) berechnet:
Dabei sind:
Grundwert der Schiefstellung
Abminderungsbeiwert für die Höhe
Abminderungsbeiwert für die Anzahl der Bauteile (m = Anzahl der Stützen)
Daraus ergibt sich das Biegemoment für die Ersatzimperfektion ei:
Zusätzliche Exzentrizität aus der Berechnung nach Theorie II. Ordnung
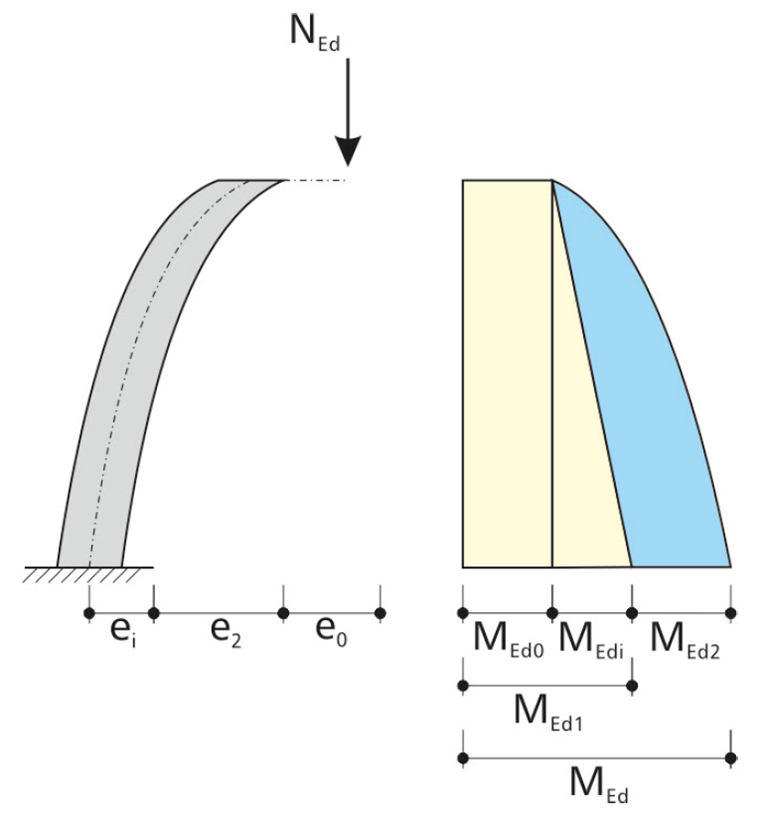
Unter der Normalkraftbelastung kommt es zu einer Krümmung der Stütze, wobei der Stützenkopf um den Weg e2 ausgelenkt wird. Daraus ergibt sich der Momentenverlauf nach Theorie II. Ordnung.
Für das Verfahren mit Nennkrümmung wird ein parabelförmiger Momentenverlauf angenommen. Die Ermittlung der Exzentrizität nach Theorie II. Ordnung wird nach EN 1992-1-1 5.8.8.2(3) vorgenommen.
Sie kann detailliert der Norm oder dem Handbuch zu (RF-)BETON Stützen entnommen werden.
Besonderheiten bei der Ermittlung der Exzentrizitäten bei zweiachsiger Lastausmitte
Für mit zweiachsiger Lastausmitte belastete Stützen darf zunächst eine getrennte Bemessung in beiden Hauptachsenrichtungen durchgeführt werden. Bei dieser Bemessung müssen die Imperfektionen ausschließlich in der Richtung angesetzt werden, in der sie zu den ungünstigsten Auswirkungen führen. Die Nachweise dürfen dann in beiden Richtungen mit der gesamten angesetzten Bewehrung geführt werden. Es gilt also auszuschließen, dass die Imperfektionen eine zweiachsige Bemessung erforderlich machen.
Um die Nachweise getrennt in beide Richtungen führen zu dürfen und keine weitere zweiachsige Biegung berücksichtigen zu müssen, müssen die Bedingungen nach Gleichung (5.38) erfüllt sein.
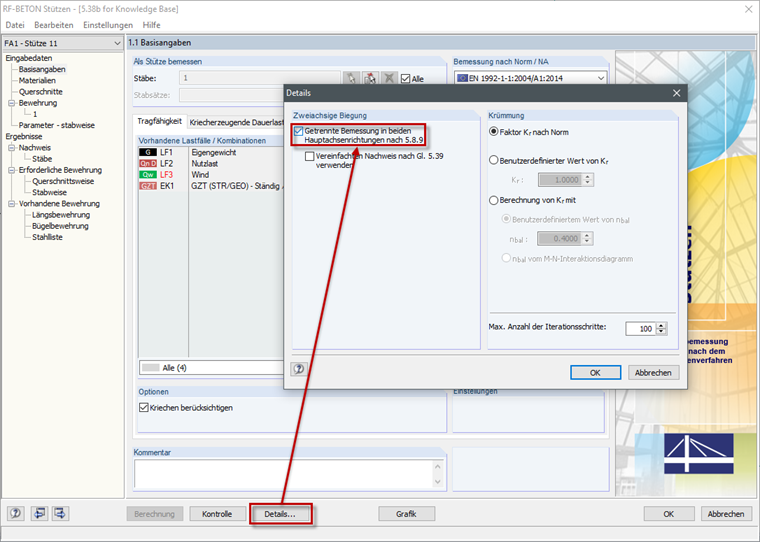
Um diesen getrennte Bemessung überhaupt führen zu können, muss die entsprechende Option in (RF-)BETON Stützen zuerst aktiviert werden.
Hierbei geht es zum einen um die Schlankheitsverhältnisse in Gleichung (5.38a):
Zum anderen muss eine der Bedingungen bezüglich der bezogenen Lastausmitten nach Gleichung (5.38b) erfüllt sein:
Dabei ist definiert:
iy und iz sind die Trägheitsradien bezogen auf die y- und z-Achse.
sind die Lastausmitten in Richtung der Achsen.
Bei der Berechnung der Bemessungsmomente MEdy und MEdz wird bei der untergeordneten Richtung die Imperfektion nicht berücksichtigt.
Die untergeordnete Richtung wird über das Verhältnis der Gesamtausmitte zur Ausmitte nach Theorie I. Ordnung ermittelt.
für die Berechnung von (5.38b).
Anderenfalls wird ei,z zu 0 gesetzt.
Ist damit eine der Bedingungen aus Gleichung (5.38b) erfüllt, so kann die Bemessung getrennt unter Vernachlässigung der Imperfektionen in die untergeordnete Richtung geführt werden. Ist (5.38b) nicht erfüllt, muss eine zweiachsige Bemessung unter Berücksichtigung sämtlicher Imperfektionen durchgeführt werden.
Beispiel Kragstütze
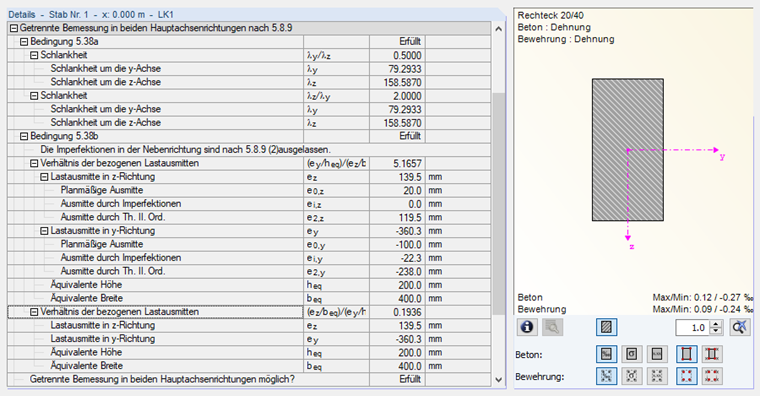
Die Exzentrizitäten aufgrund der Theorie II. Ordnung werden aus dem Programm übernommen:
e2,y = 238 mm
e2,z = 119,5 mm
Mit diesen Werten kann nun ermittelt werden, welche Richtung untergeordnet ist.
Damit kann ei,z zu 0 gesetzt werden und es ergeben sich die Werte entsprechend Bild 06.