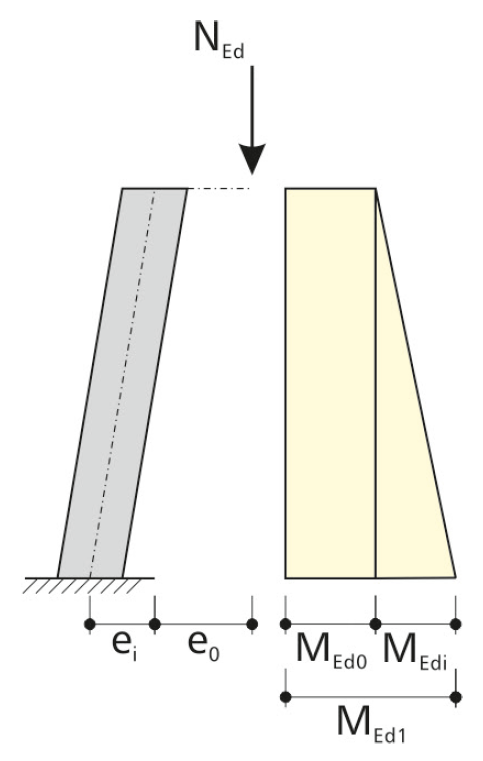
Wynikają one z planowanego wprowadzenia obciążenia mimośrodowego, niedoskonałych konstrukcji (imperfekcji geometrycznych i materiałowych) oraz dodatkowego mimośrodu z obliczeń zgodnie z teorią drugiego rzędu.
Planowane mimośrody
Mimośrody z planowanego wprowadzenia obciążenia można łatwo określić na podstawie momentów od przyłożenia obciążenia mimośrodowego. W przypadku stałego rozkładu momentów ma zastosowanie następująca zależność:
W tym przypadku minimalny mimośród wg 6.1.(4) wynosi
gdzie h jest wysokością przekroju.W przypadku zmiennego liniowo rozkładu momentu można wyznaczyć mimośród równoważny i zastosować następujący wzór:
Mimośrody należy przyporządkować do znaków. Mają ten sam znak, jeżeli powiązane momenty tworzą rozciąganie po tej samej stronie.
W przypadku dowolnego rozkładu momentu do obliczeń jest zawsze przyjmowany maksymalny mimośród, dzięki czemu z analizy nie muszą być wyłączane żadne słupy.
Mimośrody mimośrodowe od imperfekcji
W przypadku obliczania momentów zgodnie z liniową analizą statyczną należy również uwzględnić imperfekcje geometryczne i materiałowe. Można to osiągnąć poprzez zastosowanie równoważnych imperfekcji geometrycznych, które są uwzględniane jako nachylenie θi.
Mimośród jest określany w EN 1992-1-1 według wzoru (5.2):
Nachylenie θi oblicza się według wzoru (5.1):
gdzie:
Wartość podstawowa imperfekcji przechyłu
Współczynnik redukcyjny dla wysokości
Współczynnik redukcyjny dla liczby elementów konstrukcyjnych (m jest liczbą słupów)
Daje to moment zginający dla imperfekcji zastępczej ei :
Dodatkowy mimośród z obliczeń według analizy drugiego rzędu
Pod wpływem obciążenia siłą osiową następuje zakrzywienie słupa, w którym głowica słupa zostaje ugięta o ścieżkę e2. Skutkuje to rozkładem momentu zgodnie z teorią drugiego rzędu.
W przypadku metody nominalnej krzywizny przyjmuje się paraboliczny rozkład momentów. Definiowanie mimośrodu według teorii drugiego rzędu odbywa się zgodnie z EN 1992-1-1, 5.8.8.2(3).
Można je znaleźć w normie lub instrukcji obsługi (RF-)CONCRETE Columns.
Specyfika przy określaniu mimośrodów dla mimośrodu obciążenia dwukierunkowego
W przypadku słupów obciążonych dwukierunkowym mimośrodem należy najpierw przeprowadzić osobne obliczenia w obu orientacjach osi głównych. W tym przypadku imperfekcje należy zastosować wyłącznie w kierunku, w którym wywołują najbardziej niekorzystne efekty. Obliczenia można przeprowadzić w obu kierunkach, z całym zastosowanym zbrojeniem. Należy zatem wykluczyć, że imperfekcje wymagają analizy dwuosiowej.
Aby obliczenia mogły być przeprowadzane w obu kierunkach bez dalszego zginania dwukierunkowego, muszą zostać spełnione warunki określone w równaniu (5.38).
Aby możliwe było przeprowadzenie tego oddzielnego obliczenia, najpierw należy aktywować odpowiednią opcję w (RF-)CONCRETE Columns.
Z jednej strony, należy uwzględnić smukłość w równaniu (5.38a):
Z drugiej strony musi być spełniony jeden z warunków dotyczących odpowiednich mimośrodów zgodnie z równaniem (5.38a):
Gdzie
iy oraz iz są promieniami bezwładności względem osi y oraz z.
są mimośrodami obciążenia w kierunku osi.
Przy obliczaniu momentów obliczeniowych MEdy i MEdz imperfekcja dla kierunku podrzędnego nie jest uwzględniana.
Podrzędny kierunek jest określany przez stosunek mimośrodu całkowitego do mimośrodu zgodnie z liniową analizą statyczną.
do obliczenia (5.38b).
W przeciwnym razie ei,z przyjmuje wartość 0.
Jeżeli spełnia to jeden z warunków z równania (5.38b), obliczenia można przeprowadzić osobno, pomijając imperfekcje w kierunku podrzędnym. Jeżeli (punkt 5.38b) nie jest spełniony, należy przeprowadzić obliczenia dwukierunkowe z uwzględnieniem wszystkich imperfekcji.
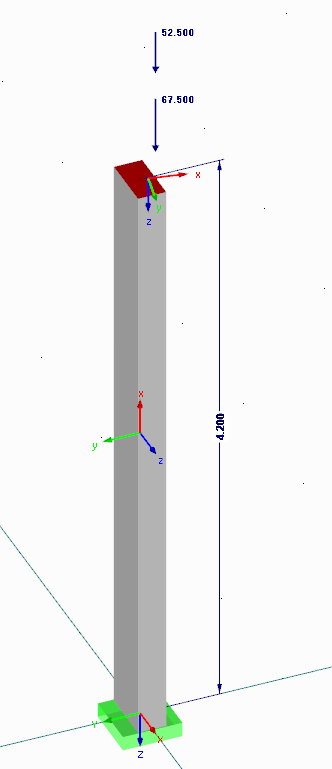
Przykładowy wspornik
Z programu importowane są mimośrody według teorii drugiego rzędu:
e2, y = 238 mm
e2, z = 119,5 mm
Na podstawie tych wartości można teraz określić, który kierunek jest podporządkowany.
W ten sposób ei, z można ustawić na 0, a wartości zgodnie z wynikiem na rys. 06.