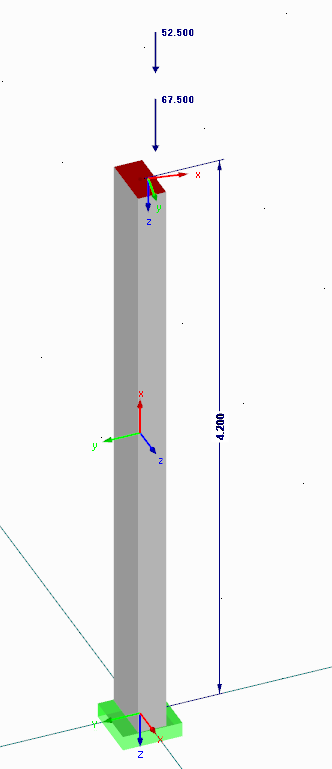
Estos son el resultado de una introducción de carga excéntrica planificada, estructuras imperfectas (imperfecciones geométricas y de materiales) y una excentricidad adicional del cálculo según el análisis de segundo orden.
Excentricidades planificadas
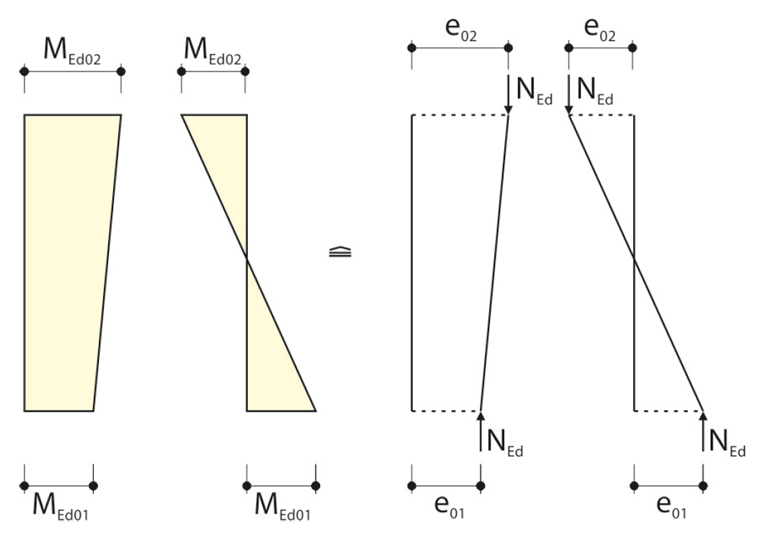
Las excentricidades de la introducción de carga excéntrica planificada se pueden determinar fácilmente con los momentos debidos a una aplicación de carga excéntrica. Para una distribución de momentos constante, se aplica la siguiente relación:
En este caso, la excentricidad mínima según 6.1.(4) es
donde h es el canto de la sección.Para una distribución de momentos linealmente variable, se puede determinar una excentricidad equivalente y aplicar la siguiente fórmula:
Las excentricidades se deben aplicar con signos algebraicos. Tienen el mismo signo si los momentos relacionados crean tracción en el mismo lado.
Si hay alguna distribución de momentos, siempre se usa la excentricidad máxima para el cálculo, de modo que no se deben excluir pilares del análisis.
Excentricidades no intencionadas debidas a imperfecciones
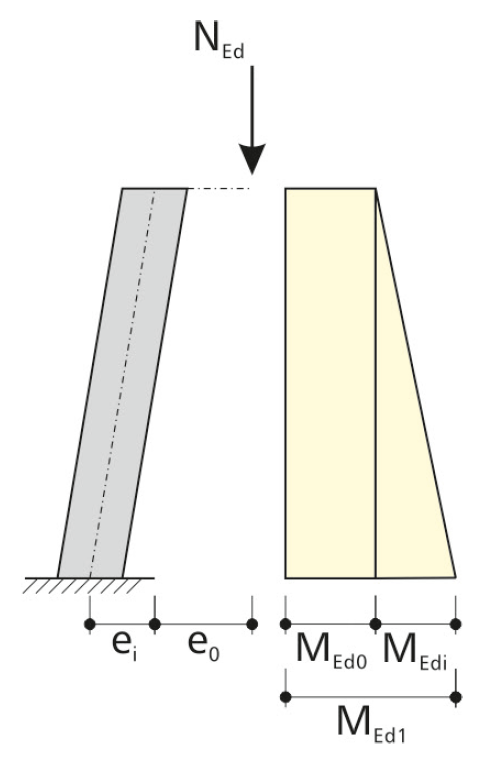
Para el cálculo de los momentos según el análisis estático lineal, también se deben tener en cuenta las imperfecciones geométricas y del material. Esto puede ocurrir al aplicar las imperfecciones geométricas equivalentes que se consideran, como la inclinación θi.
La excentricidad se determina en EN 1992-1-1 según la fórmula (5.2):
Se calcula la inclinación θi según la fórmula (5.1):
Donde:
Valor básico de la imperfección de verticalidad
Coeficiente de reducción para la altura
Coeficiente de reducción para el número de componentes estructurales (m es el número de pilares)
De aquí se obtiene un momento flector para la imperfección equivalente ei:
Excentricidad adicional del cálculo según el análisis de segundo orden
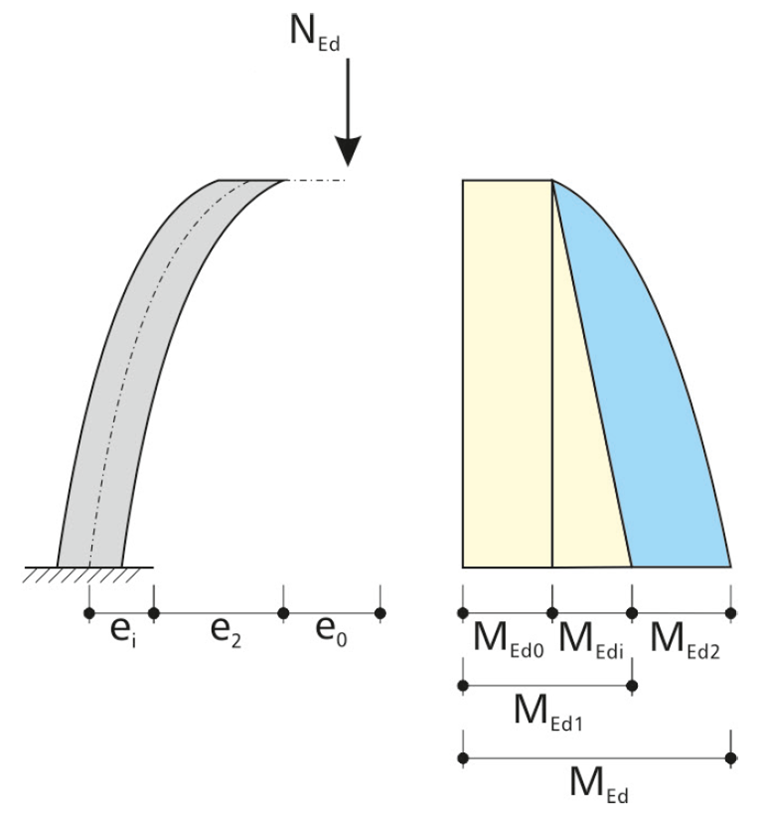
Bajo la carga de esfuerzo axil, se da una curvatura del pilar con un desvío de la cabeza del pilar de e2. Esto da como resultado la distribución de momentos según la teoría de segundo orden.
Para el método basado en curvatura nominal, se asume una distribución del momento parabólica. La determinación de la excentricidad según la teoría de segundo orden se realiza según EN 1992-1-1 5.8.8.2(3).
Se puede encontrar en detalle en la norma o en el manual para (RF-)CONCRETE Columns.
Detalles al determinar las excentricidades para la excentricidad de carga biaxial
Para pilares cargados con una excentricidad de carga biaxial, primero se debe realizar un cálculo por separado en ambas orientaciones del eje principal. Para este cálculo, las imperfecciones se deben aplicar exclusivamente en la dirección donde conducen a los efectos más desfavorables. Los cálculos se pueden realizar en ambas direcciones con toda la armadura aplicada. Por lo tanto, se trata de descartar que las imperfecciones necesiten un análisis biaxial.
Para poder realizar los cálculos en ambas direcciones sin tener que considerar una flexión biaxial adicional, se deben cumplir las condiciones indicadas en la ecuación (5.38).
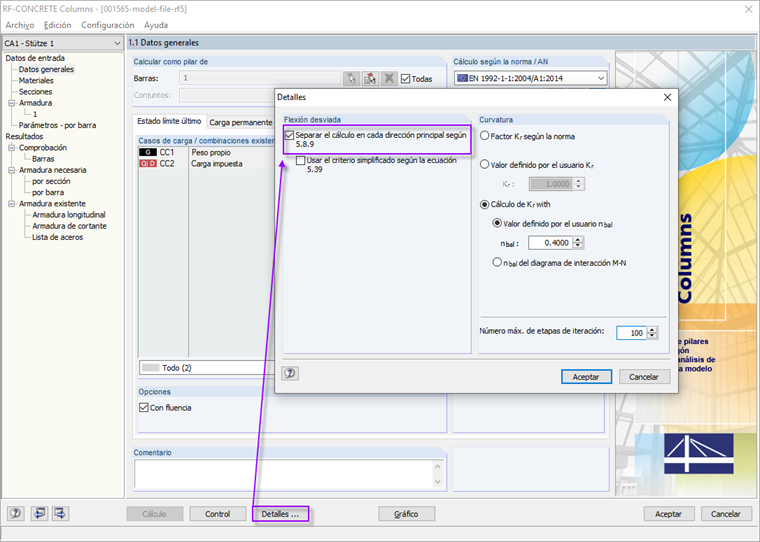
Para poder realizar este cálculo por separado, primero se debe activar la opción correspondiente en (RF-)CONCRETE Columns.
Por un lado, se debe tener en cuenta la relación de esbeltez en la ecuación (5.38a):
Por otro lado, se debe cumplir una de las condiciones con respecto a las excentricidades de carga relacionadas según la ecuación (5.38a):
Donde
iy e iz son los radios del giro en relación con el ejes y y z.
son las excentricidades de carga en la dirección de los ejes.
Cuando se calculan los momentos de cálculo MEdy y MEdz, no se tiene en cuenta la imperfección para la dirección subordinada.
La dirección subordinada se determina mediante la relación entre la excentricidad total y la excentricidad según el análisis estático lineal.
para el cálculo de (5.38b).
De lo contrario, se establece ei,z con un valor de 0.
Si esto cumple una de las condiciones de la ecuación (5.38b), el cálculo se puede realizar por separado mientras se ignoran las imperfecciones en la dirección subordinada. Si no se cumple (5.38b), se debe realizar un cálculo biaxial considerando todas las imperfecciones.
Soporte de ejemplo
Las excentricidades debidas a la teoría de segundo orden se importan del programa:
e2,y = 238 mm
e2,z = 119,5 mm
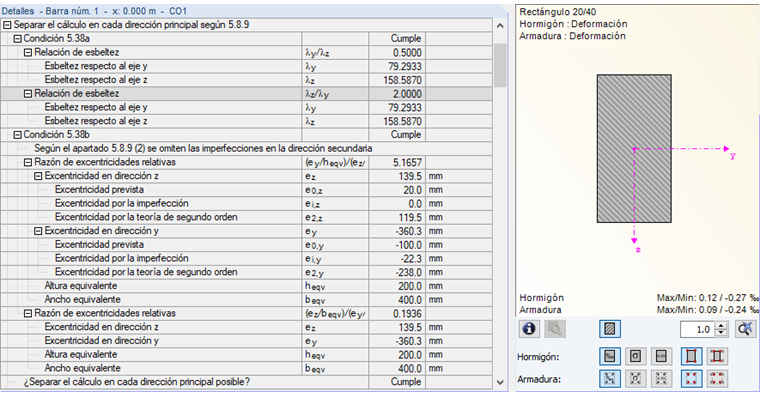
Con estos valores, ahora se puede determinar qué dirección está subordinada.
Por lo tanto, se puede establecer ei,z con un valor de 0, con lo que se obtienen los valores según la figura 06.