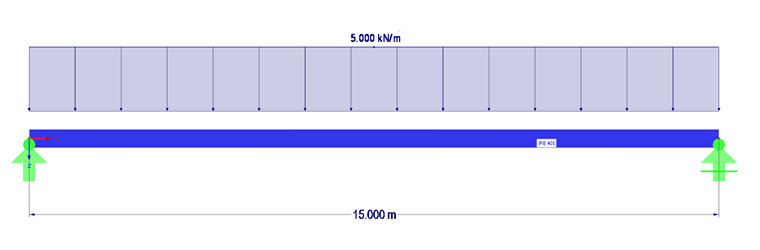
Конструктивная система и нагрузки
Данная модель представляет собой однопролетную балку длиной 15 м. Сечение балки - IPE 400 из стали марки S355. Нагрузка составляет 5 кН/м. Собственный вес не учитывается.
Расчет без стабилизации
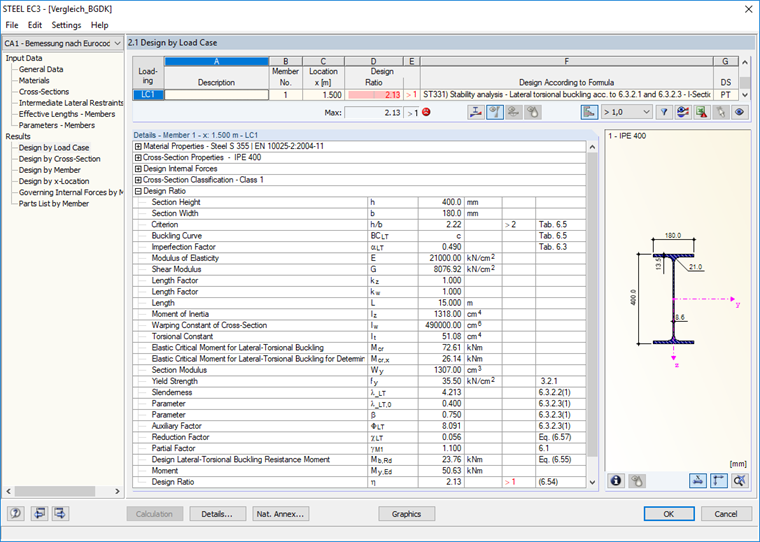
Расчет можно выполнить со стандартными настройками (однопролетная балка с вильчатой опорой) в дополнительном модуле RF-/STEEL EC3 по немецкому национальному приложению, условия приложения не будут выполнены.
Критический момент при продольном изгибе в этом случае составляет всего лишь 72,61 кНм, это значение можно подтвердить общими формулами из технической литературы.
Расчет со стабилизацией в верхнем поясе
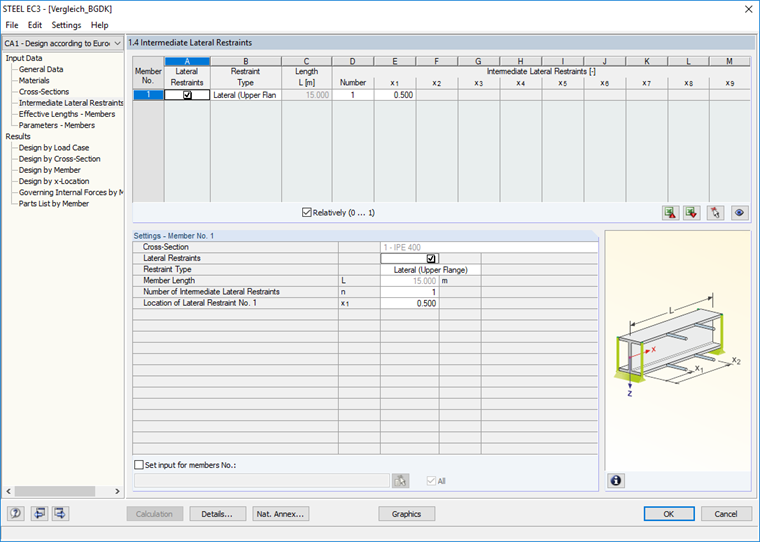
С помощью виртуального поперечного стержня в середине верхнего пояса исключается его смещение.
Данную стабилизацию можно обеспечить в RF-/STEEL EC3 с помощью боковой промежуточной опоры, при этом нет необходимости разделять стержень.
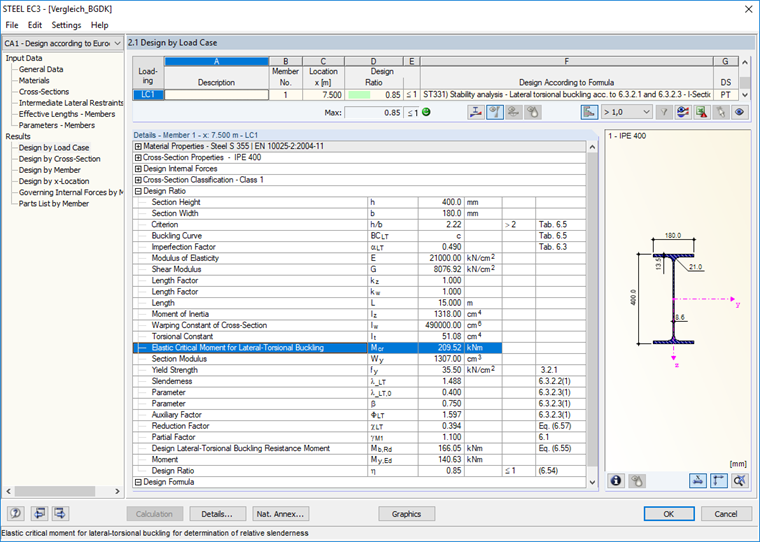
Последующий расчет по разделу 6.3.2.3 нормы EN 1993-1-1 [1] содержит успешный результат, критический момент при изгибе равен 209,52 кНм.
Сравнение с общим методом расчета блока стержней
В следующем шаге выполним расчет общим методом в качестве расчета блока стержней. Скопируем стержень в направлении Y, включая опоры и нагрузку, разделим стержень один раз в середине и зададим блок стержней.
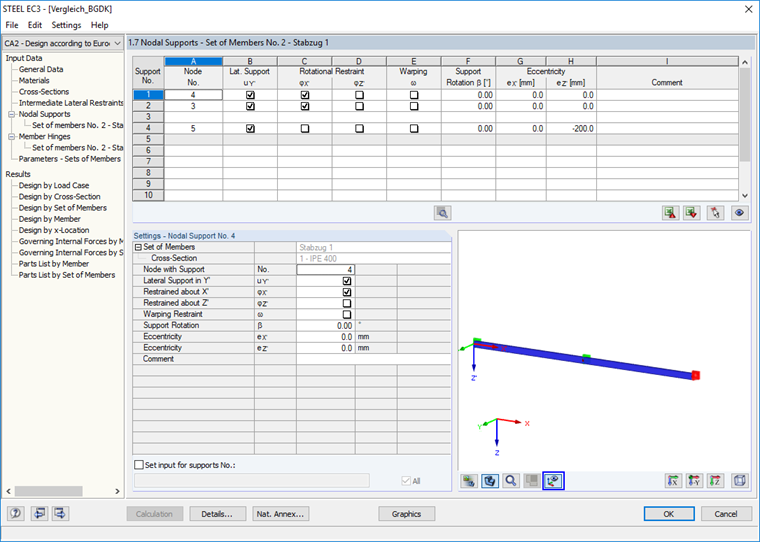
В новом расчетном случае в RF-/STEEL EC3 выберем этот блок стержней для расчета. Вместо диалогового окна "1.5 Полезные длины - стержни" появится окно "1.7 Узловые опоры". По умолчанию в начале и на конце расчетного блока стержней заданы две опоры с держателями φx' и uy'.
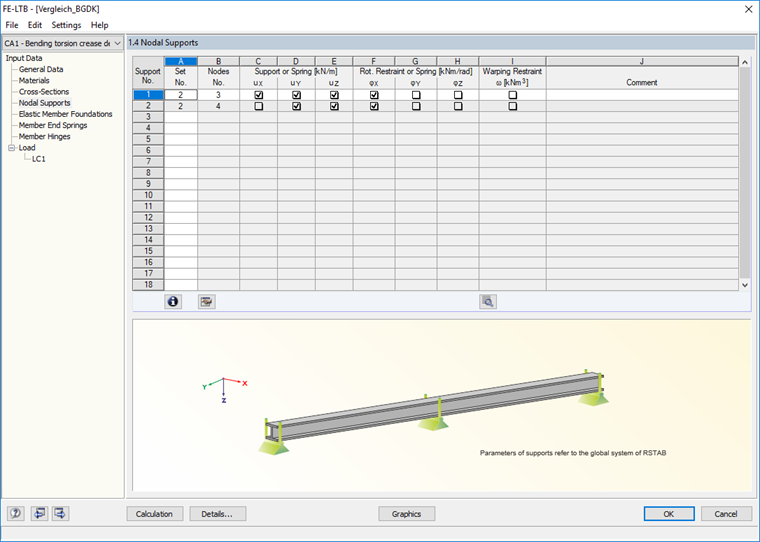
Чтобы стабилизировать стержень, необходимо посередине создать еще одну опору и задать эксцентриситет -200 мм в локальном направлении z.
Опоры можно легко отобразить с помощью соответствующей кнопки в графическом окне частичного изображения.
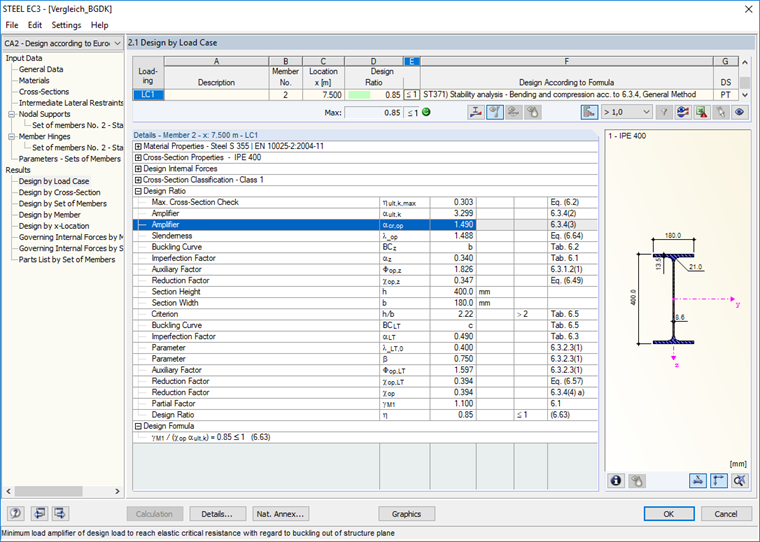
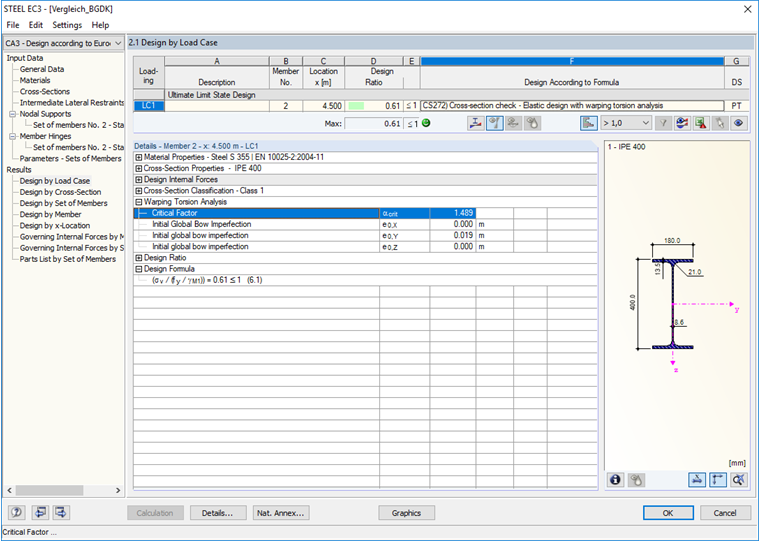
Данный расчет выполнен успешно, значение критической нагрузки равно 1,49.
На основе максимального момента мы можем затем определить критический момент при продольном изгибе, равный 209,54 кНм, который соответствует последнему расчету.
Коэффициент гибкости балки, который потребуется для учета несовершенства в следующем разделе, равен 1,488.
Сравнение с анализом кручения
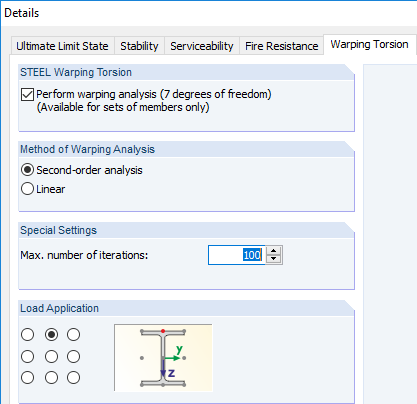
В следующем шаге сравним критическую силу с анализом кручения, это означает, что вместо четырех степеней свободы мы применим семь степеней свободы.
Во вкладке «Кручение с депланацией», в диалоговом окне «Подробности» нужно активировать соответствующее модульное расширение.
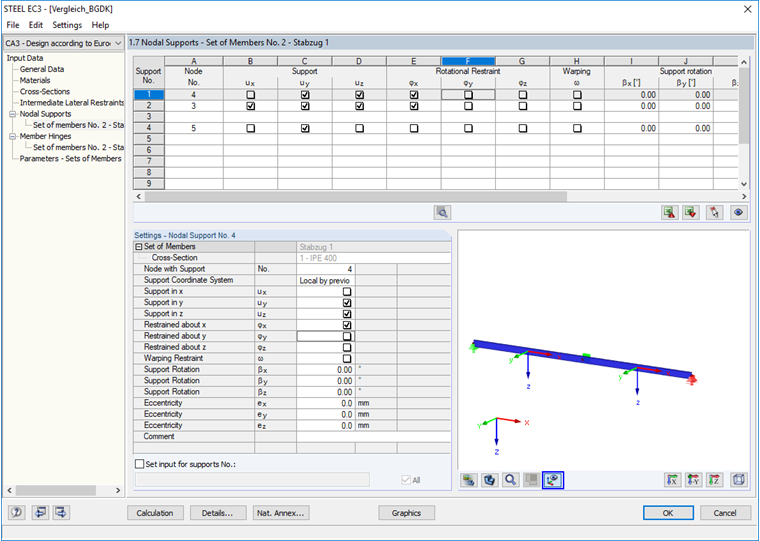
Как и в случае с расчетом по 6.3.4 нормы EN 1993-1-1, необходимо проверить узловые опоры и при необходимости изменить их.
В окне 1.13 введем значение несовершенства L/400.
Дальнейший расчет более приемлем со значением критической нагрузки 1,489, которое соответствует предыдущим расчетам.
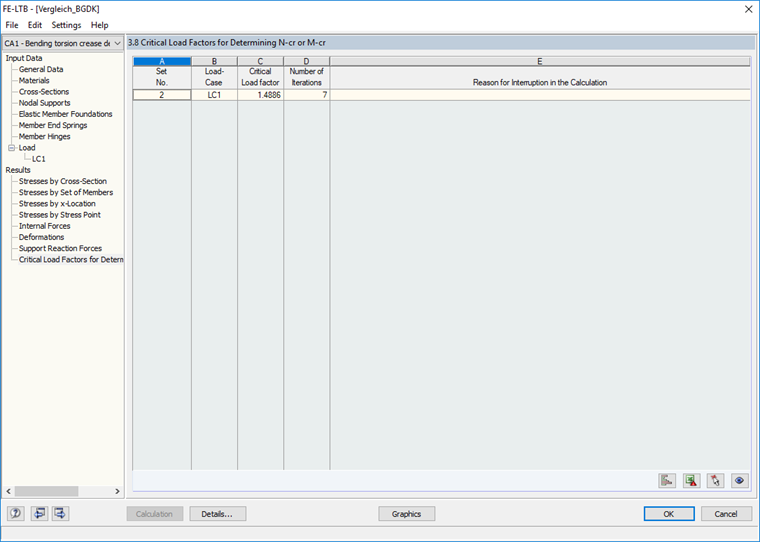
Сравнение с дополнительным модулем RF-/FE-LTB
В последнем шаге рассчитаем однопролетную балку (блок стержней) в дополнительном модуле RF-/FE-LTB, а затем сравним критическую нагрузку.
Импортируем напрямую в RF/FE-LTB узловые опоры, заданные для блока стержней.
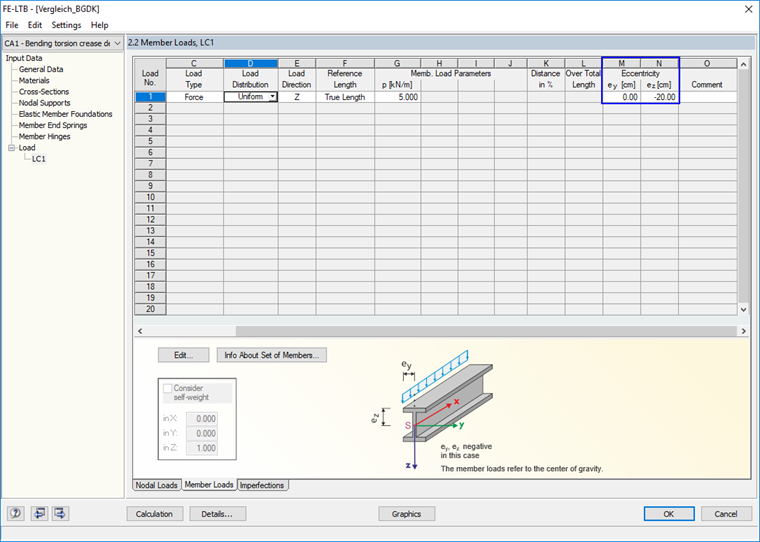
В этом случае мы не можем определить эксцентриситет, поэтому промежуточную опору не будем задавать в качестве узловой опоры, а зададим в качестве пружины на конце стержня в окне 1.6.
При вводе нагрузки необходимо обратить внимание на учет эксцентриситета, в противном случае мы получим слишком благоприятный результат расчета.
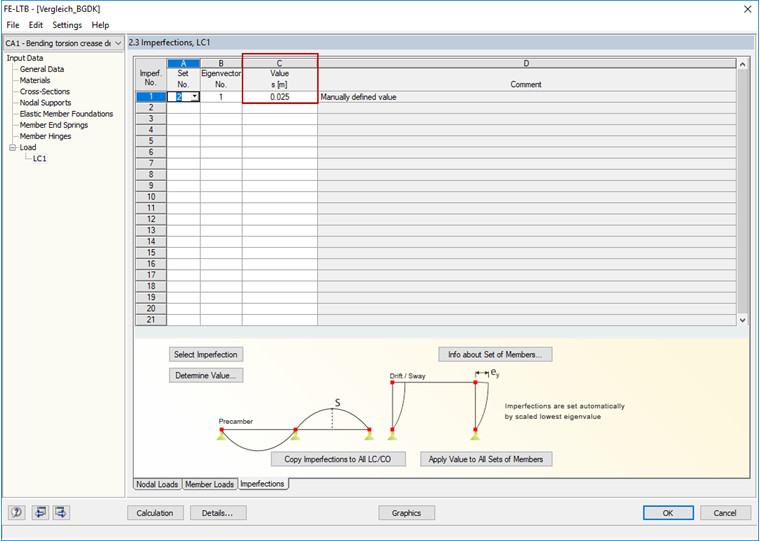
Несовершенство для первой собственной формы задается вручную и равно 1,875 см.
Результатом окончательного расчета будет значение критической силы, равное 1,489 и соответствующее всем предыдущим расчетам.