1846x

001617

Dipl.-Ing. Thomas Günthel

2020-01-10

Выбор узлов вдоль линии с помощью интерфейса COM

При считывании результатов поверхности посредством интерфейса COM, получит пользователь одномерное поле со всеми результатами в отдельных узлах КЭ или точках сетки. Чтобы получить результаты по краю поверхности или вдоль линии, находящейся внутри поверхности, необходимо сначала отфильтровать результаты для области линии. В следующей статье будет представлена функция, благодаря которой можно выполнить данную задачу.

Теоретические основы расчета промежутков

Для того, чтобы найти узлы сетки КЭ, находящиеся близко линии или на линии, необходимо рассчитать промежуток от узла до линии. При этом нам дана линия с начальной и конечной точкой (N₀ и N₁), а также точка P, отступ которой от линии необходимо определить. Распространенным способом расчета данного промежутка является создание плоскости, которая проходит через точку P и перпендикулярна прямой. Для этого необходимо сначала составить подходящее уравнение линии. В этом случае рекомендуется применить параметрическую форму, которая содержит направляющий вектор v. Затем его можно применить для составления уравнения плоскости.

Gerade G : \overset{⇀}{X} = \overset{⇀}{A} s \cdot \overset{⇀}{v} (1)

mit

A = N_{0}

v = N_{1} - N_{0}

Уравнение прямой

Для опорного вектора A используется начальная точка (радиусный вектор) линии, а для направляющего вектора v - разность двух радиусных векторов. В качестве уравнения плоскости будет применена нормальная форма по указанной выше причине.

Ebene E : 0 = (\overset{⇀}{X} - \overset{⇀}{P}) \cdot \overset{⇀}{n} (2)

mit

\overset{⇀}{n} = \overset{⇀}{v}

\overset{⇀}{P} = \overset{⇀}{P_{res}}

Уравнение плоскости

Опорный вектор P в данном случае - это результативная точка P_res, подлежащая анализу. Вектор нормали является направляющим вектором прямой, поскольку плоскость перпендикулярна прямой. Прежде чем рассчитать отступ, необходимо определить коэффициент s прямой, по которой плоскость пересекает прямую. Для этого радиусный вектор X в уравнении плоскости заменяется уравнением прямой.

(1) in (2) : 0 = ((\overset{⇀}{A} s \cdot \overset{⇀}{v}) - \overset{⇀}{P}) \cdot \overset{⇀}{n} (3)

Замена радиусного вектора X в уравнении плоскости уравнением прямой

Преобразовать в s и начать с

\overset{⇀}{n} = \overset{⇀}{v}

Нормальный вектор

мы получим следующее уравнение.

s = \frac{(\overset{⇀}{P} - \overset{⇀}{A}) \cdot \overset{⇀}{v}}{(\overset{⇀}{v} \cdot \overset{⇀}{v})} (4)

Коэффициент s

Таким образом, теперь можно с помощью уравнения 1 определить точку пересечения S.

\overset{⇀}{S} = \overset{⇀}{A} s \cdot \overset{⇀}{v} (5)

Точка пересечения S

Промежуток d между S и P_res определяется посредством величины вектора, соответствующей разности между ними.

d = |\overset{⇀}{P_{res}} - \overset{⇀}{S}| (6)

Расстояние d между S и P_res

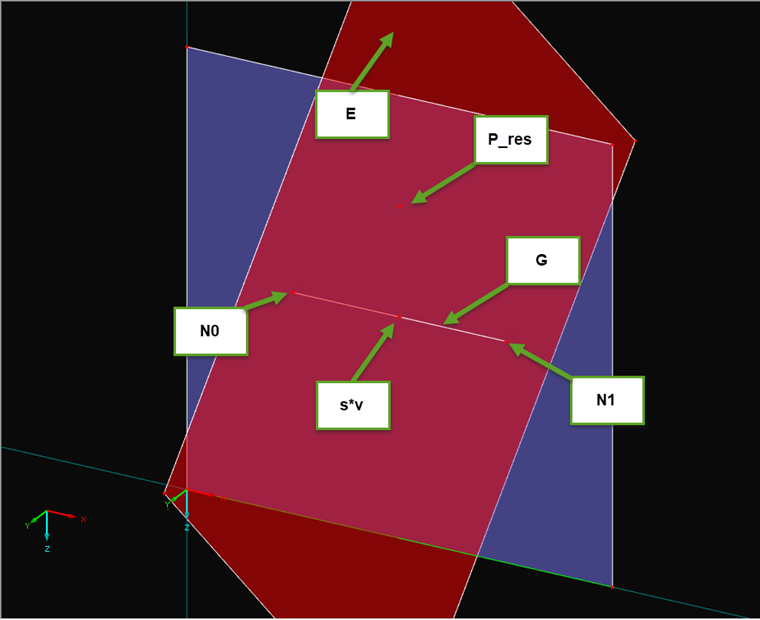
На рисунке 01 схематически показаны все перечисленные элементы. Поверхность синего цвета - это анализируемая поверхность, а поверхность красного цвета представляет собой плоскость разреза, которая задается точкой P_res и направляющим вектором

\overset{⇀}{v}

Вектор направления

. Коэффициент s на рисунке равен в точности 0,5, поэтому пересечение плоскости и линии находится как раз в центре линии.

1 Схематическое изображение компонентов для расчета отступа

Выполнение расчета промежутка в программе

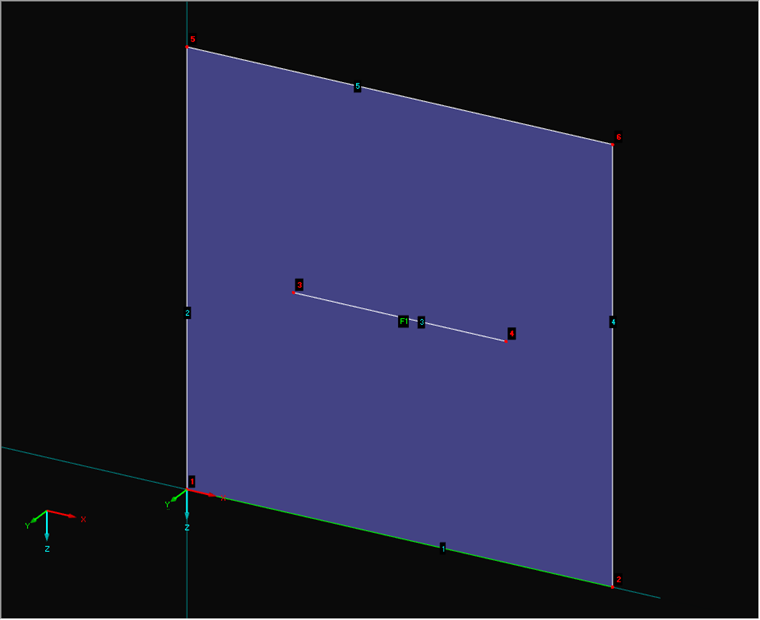
После составления формул можно создать соответствующую программу. Для перевода применяется EXCEL VBA. На рисунке 02 показана нумерация элементов.

2 Модель для расчета примера

Сначала необходимо подключится к программе RFEM. Затем выберем интерфейс для данных модели. Поскольку этот алгоритм уже был пояснен в различных статьях (см. ссылки), не будем на нем останавливаться подробно. Ниже приведен исходный код для запуска программы.

Sub selection_test2 ()
    
    Размер line_no как целое число
    Размеры Surface_no как целое число
    Размер loadcase_no как целое число
    Размер d_tol как двойный
    line_no = 11
    Surface_no = 1
    loadcase_no = 1
    d_tol = 0,001
    
    '   get interface from the opened model and lock the licence/program
    Размеры iModel как RFEM5.IModel2
    Set iModel = GetObject(, "RFEM5.Model")
    iModel.GetApplication.LockLicense
    
On Error GoTo e
    
    Dim iModelData As RFEM5.IModelData2
    Set iModelData = iModel.GetModelData

Перед запуском программы сначала необходимо задать переменные параметры. К ним относятся номер строки line_no, в которой требуется выполнить поиск результатов, и, конечно, номер поверхности surface_no, на которой расположена линия. Кроме того, необходимо задать номер нагружения loadcase_no, к которому относятся результаты. Поскольку выполняется численное вычисление с ограниченной точностью, требуется задать допуск d_tol, который определяет максимальное расстояние между линией и узлом. В данном примере применен допуск, равный один миллиметр.

Так как теперь у нас имеется интерфейс для данных модели (IModelData), то можно сначала выполнить поиск линии, и тем самым ее начальной и конечной точки.

   ' получить линию
    Размер ILin как RFEM5.ILine
    Задать ILin = iModelData.GetLine(line_no, AtNo)
    Размер лин как RFEM5.RfLine
    lin = ILin.GetData
   
    
    ' получить узлы из линии
    Размер n(0 до 1) Как RFEM5.Node
    
    Dim ints() как целое число
    ints = strToIntArr (lin.NodeList)
    
    Размер в RFEM5.INode
    Задать iNd = iModelData.GetNode(ints(0),AtNo)
    n(0) = iNd.GetData
    Задать iNd = iModelData.GetNode (ints (UBOUND (int, 1)), AtNo)
    n (1) = iNd.GetData
    
    Задать iNd = ничего

Выберем узлы и линии по отдельности прямо через их интерфейс (INode или ILine). Чтобы извлечь номера узлов из строки символов (RfLine.NodeList), применяется функция strToIntArr, описанная в другой статье (см. ссылки). Она преобразует строку символов в цифровое поле.

С заданными точками линии

\overset{⇀}{N_{0}}

Начальная точка

(начальная точка) и

\overset{⇀}{N_{1}}

Конечная точка

(Конечная точка) можно задать первые параметры уравнения.

    Размер v As RFEM5.Point3D
    vX = N(1).X - N(0).X
    vY = N(1).Y - N(0).Y
    vZ = N(1).Z - N(0).Z
    
    Размер A как RFEM5.Point3D
    АКС = N(0).X
    AY = N (0).Y
    AZ = N(0).Z
    
    Размер v2 как двойный
    v2 = vX ^ 2 + vY ^ 2 + vZ ^ 2
    
    Размер P_res как RFEM5.Point3D
    Размеры двойные
    Размер d как двойный

Он становится направляющим вектором

\overset{⇀}{v}

Вектор направления

(v) опорный вектор

\overset{⇀}{A}

Опорный вектор

(A) и масштабное произведение направляющего вектора

\overset{⇀}{v} \cdot \overset{⇀}{v}

Масштабное произведение направляющего вектора

(v2) рассчитано или подготовлено. Кроме того, нужно определить переменные P_res (P_res) для результативной точки и s для множителя из уравнения линии (1).

Расчет промежутка с помощью цикла

В данном примере была выбрана обработка результатов на основе узлов сетки КЭ. Проверка промежутка происходит с помощью цикла над полем результатов. Сначала необходимо открыть данные результаты через интерфейс ICalculation2, а затем - IResults. Внутри цикла а первую очередь определяется точка P_res с помощью координат конечного значения (для наглядности). Затем мы можем выполнить прямой расчет уравнения (4). После вычисления s можно проверить, является ли значение меньше нуля или больше единицы, так как эти значения лежат вне прямой или до и после прямой. Если значение находится в данном интервале, то промежуток рассчитывается по уравнению (6).

    ' получить результаты в fe-узлах
    Dim iCalc As ICalculation2
    Set iCalc = iModel.GetCalculation
    
    Размеры iRes как RFEM5.IResults
    Задать iRes = iCalc.GetResultsInFeNodes(LoadCaseType, loadcase_no)
    
    Размер серф BaStr() As RFEM5.SurfaceBasicStresses
    surfaceBastr = iRes.GetSurfaceBasicStresses(surface_no, AtNo)
    
    ' цикл по напряжениям и расчёт расстояния до линии
    Dim i As Integer
    Для i = 0 To UBOUND(surfBaStr, 1)
        P_res.X = surfaceBastr(i).Coordinates.X
        P_res.Y = surfaceBastr(i).Coordinates.Y
        P_res.Z = surfaceBastr(i).Coordinates.Z
        ' рассчитать коэффициент для уравнения линии пересечения
        s = ((P_res.XA.X)*vX + (P_res.YA.Y)*vY + (P_res.ZA.Z)*vZ)/v2
        
        Если s <= 1 + d_tol И s >= 0 - d_tol Тогда
            ' рассчитать расстояние до точки пересечения и fe-узла
            d = ((P_res.X-(A.X+s*vX))^2
                 +(P_res.Y-(A.Y+s*vY))^2
                 +(P_res.Z-(A.Z+s*vZ))^2)^0,5
            
            Если (d < d_tol), то
                ' здесь можно обработать найденную точку результата
            End If
        End If
        
    Следующий i

Для проверки коэффициента s и промежутка d применяется допустимое отклонение, для того, чтобы небольшие неточности не приводили к исключению результата.

Результаты программы

Найденные программой значения отображаются в таблице с округлением до двух десятичных знаков.

σ_y+ [Н/мм²]	Коэффициент s [-]
21,90	0,0
17,28	0,1
12,79	0,2
8,43	0,3
4,17	0,4
-0,04	0,5
-4,25	0,6
-8,51	0,7
-12,87	0,8
-17,36	0,9
-21,98	1,0

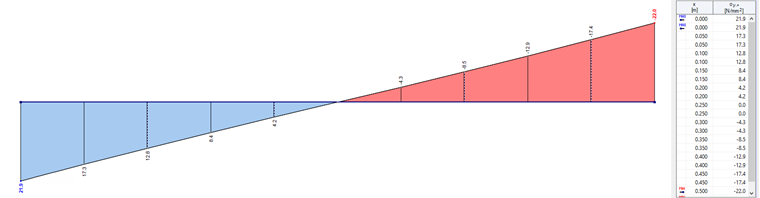
Для сравнения, значения диаграммы результатов на соответствующей линии показаны на рисунке 03.

3 Диаграмма результатов на анализируемой линии

Очевидно, что значения одинаковы и получено совпадение на 100%, то есть все значения были найдены на линии.

Заключение

С помощью векторного вычисления была создана программа, которая дает возможность найти узлы, расположенные вдоль линии. На основе данного алгоритма можно производить не только поиск полученных результатов, но и любых других геометрических элементов. Это особенно ценно, так как объективно невозможный в интерфейсе COM визуальный выбор таким образом становится возможным иным способом через функцию. Например, у программ, которые полностью работают в фоновом режиме, можно таким образом выполнить автоматическую оценку результатов.

База знаний

KB 001617 | Выбор узлов вдоль линии с помощью интерфейса COM

Автор

Г-н Гюнтель осуществляет техническую поддержку пользователей Dlubal Software.

Ссылки

Скачивания

Модель из технической статьи | Файл RFEM 5

1,11 MB

Файл EXCEL с макросом

35,44 KB

;