Свободная длина продольного изгиба в RFEM 6
Для включения расчета на устойчивость в результаты расчета стальных конструкций, важно перед выполнением расчета присвоить стержням свободные длины. В RFEM 6 свободная длина не является локальной настройкой только одного стержня. Каждая свободная длина, заданная в программе, может быть присвоена одновременно нескольким стержням или блокам стержней.
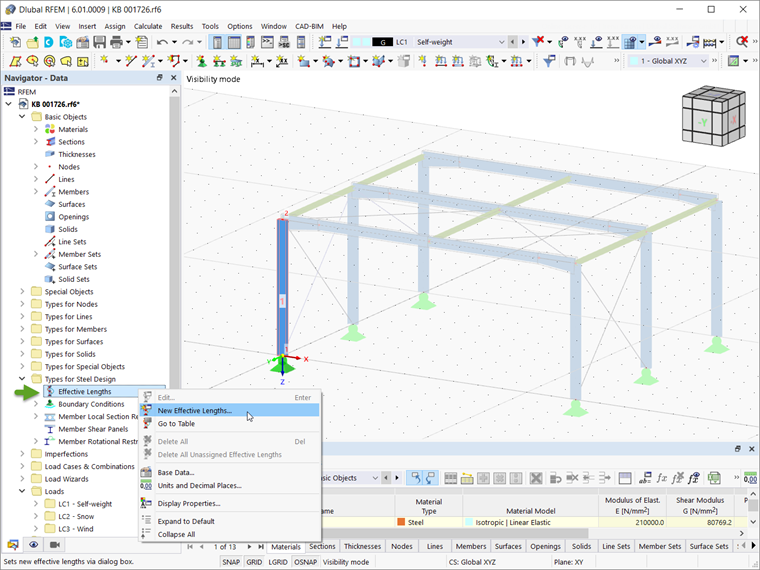
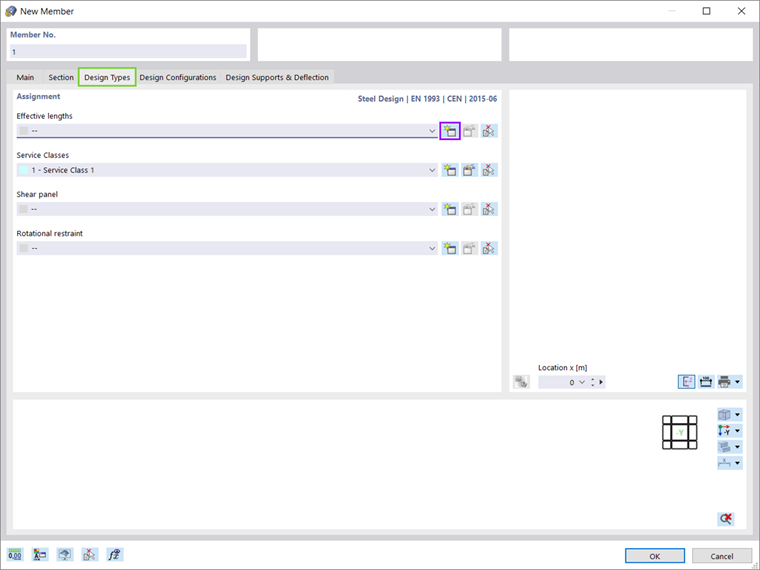
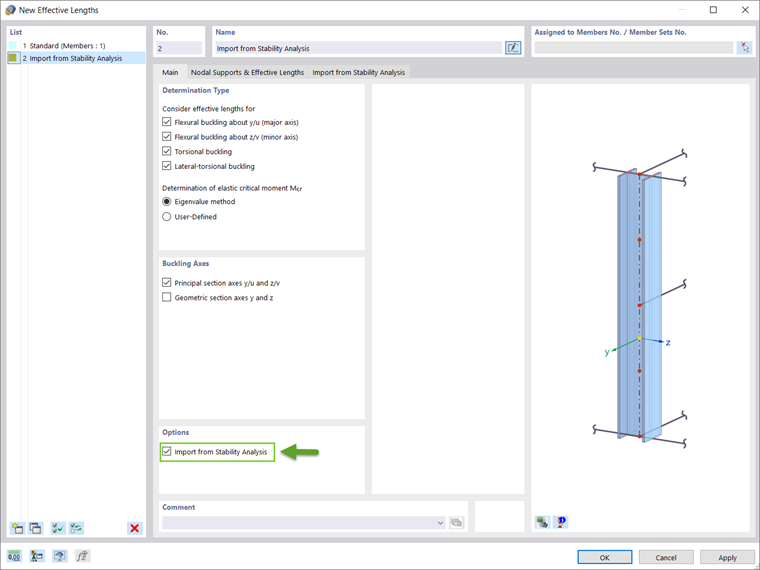
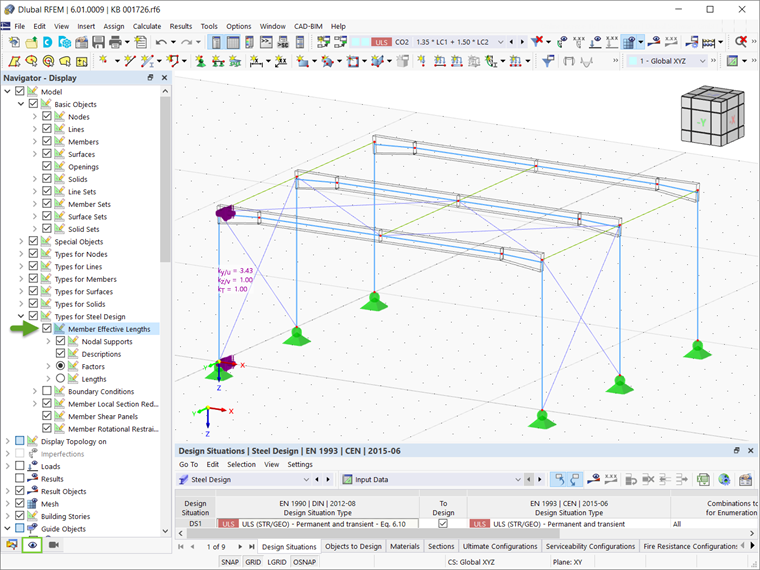
Если аддон Расчет стальных конструкций активирован в Основных данных модели, то новые свободные длины можно задать во вкладке Данные в навигаторе (рисунок 1). Другой возможностью является ввод свободной длины во вкладке Типы расчета в окне Новый стержень (рисунок 2).
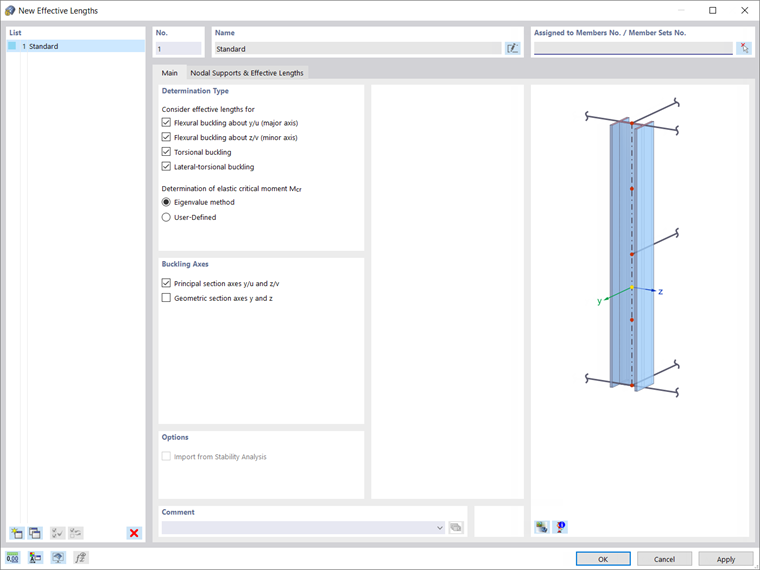
Независимо от способа задания, свободную длину можно учесть в потере устойчивости при изгибе вокруг главной и второстепенной оси, а также в потере устойчивости при кручении и при продольном изгибе с кручением (рисунок 3).
1. Определение расчетной длины с помощью узловых опор и коэффициентов расчетной длины
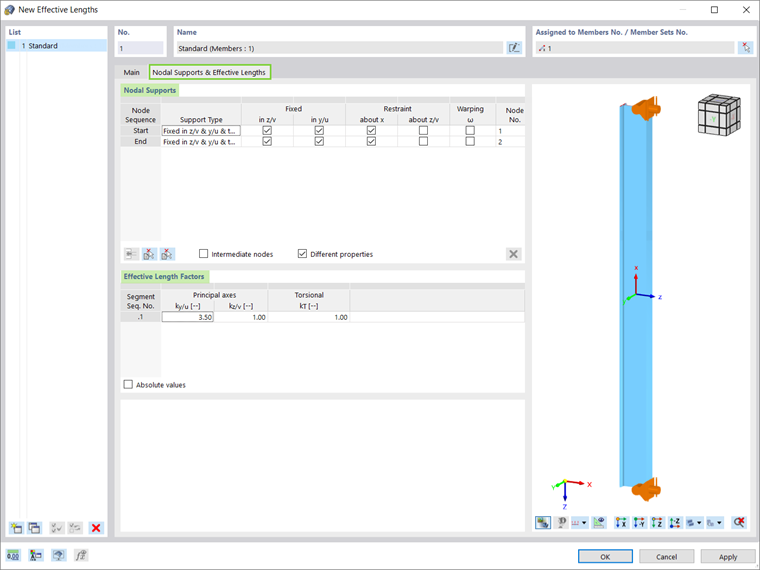
Сначала мы покажем, как задать свободную длину с помощью учета узловых опор и коэффициентов свободной длины с учетом условий опирания стержня (рисунок 4).
Принимая во внимание условия опирания колонны 1, необходимо задать узловые опоры, защемленные в двух главных направлениях z/v и y/u, а также кручение (защемление вокруг оси x) только в начале и на конце данного стержня. Поскольку промежуточные опоры, разделяющие стержень на сегменты разной длины, отсутствуют, коэффициенты свободной длины следует рассчитать вручную и скорректировать для всей длины стержня в качестве одного сегмента.
В нашем примере колонна соединена с горизонтальной балкой в виде рамы, и поэтому ожидаемая свободная длина потери устойчивости для главной оси y равна приблизительно 3,5, тогда как коэффициент свободной длины для потери устойчивости при изгибе вне плоскости равен 1.
2. Импорт свободной длины из расчета на устойчивость
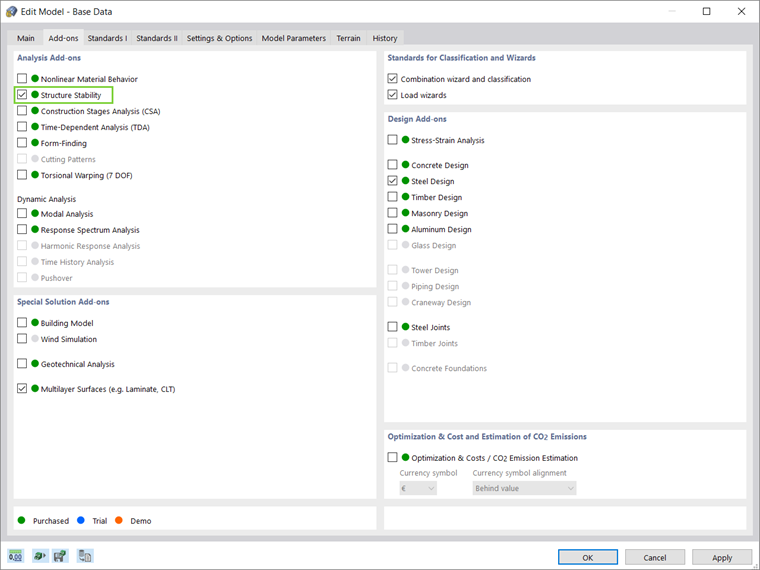
RFEM 6 предлагает еще одну возможность для задания свободных длин стержней: импорт свободной длины из расчета на устойчивость. Для этого необходимо активировать аддон Устойчивость конструкции (рисунок 5).
В данном случае необходимо выполнить расчет на устойчивость для того, чтобы получить соответствующие собственные формы и соответствующие свободные длины отдельных стержней. Затем свободные длины могут быть присвоены соответствующим стержням и могут быть учтены в расчете стальной конструкции.
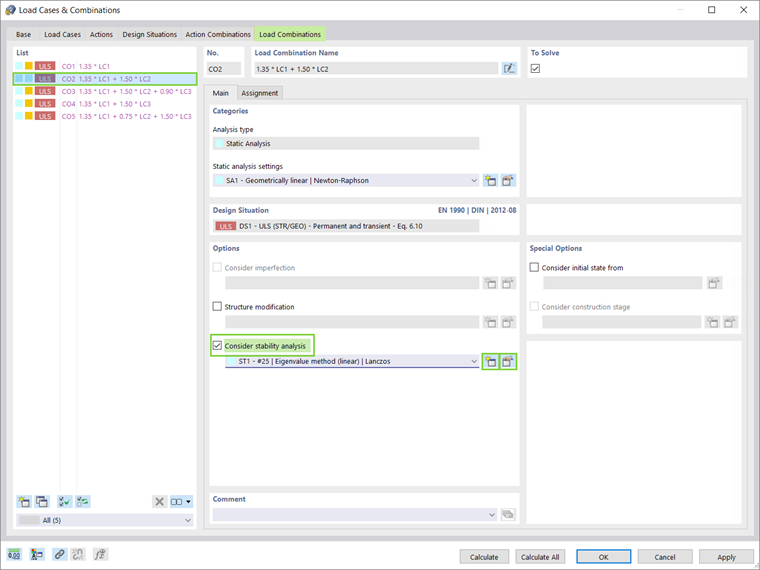
В RFEM 6 расчет на устойчивость учитывается в отдельных загружениях и сочетаниях нагрузок, как показано на рисунке 6. В нашем примере будет рассмотрен расчет на устойчивость для сочетания нагрузок 2 (собственный вес и снег) из-за связанного с ним сжатия.
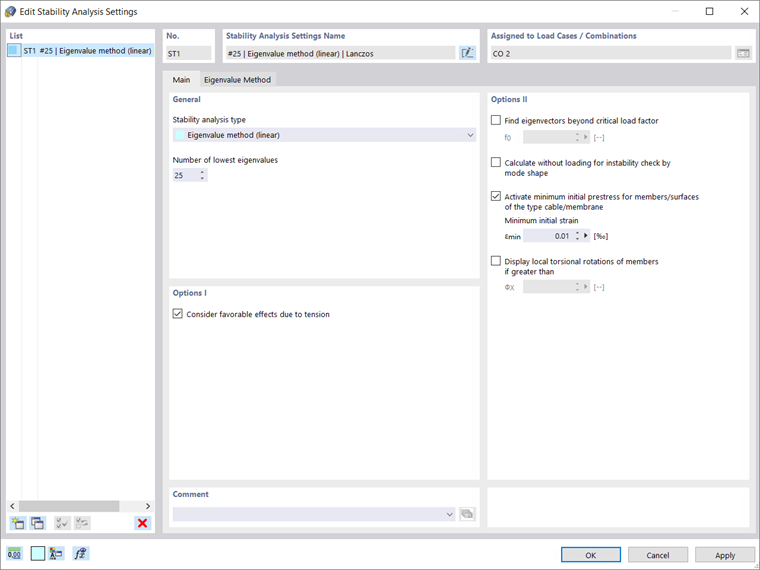
Настройки расчета на устойчивость можно легко задать в окне, показанном на рисунке 7. Например, тип расчета на устойчивость (метод собственных значений, инкрементальный метод с анализом собственных значений, инкрементальный метод без анализа собственных значений), количество наименьших собственных чисел и возможность учета благоприятных эффектов от растяжения должны быть скорректированы в случае, если предпочитается один из методов собственных значений (Ланцоша, корни характеристического полинома, итерация подпространства или итерация ICG).
Аналогичным образом должны быть заданы параметры для пошагового увеличения нагрузки, если предпочтение отдается инкрементальному методу.
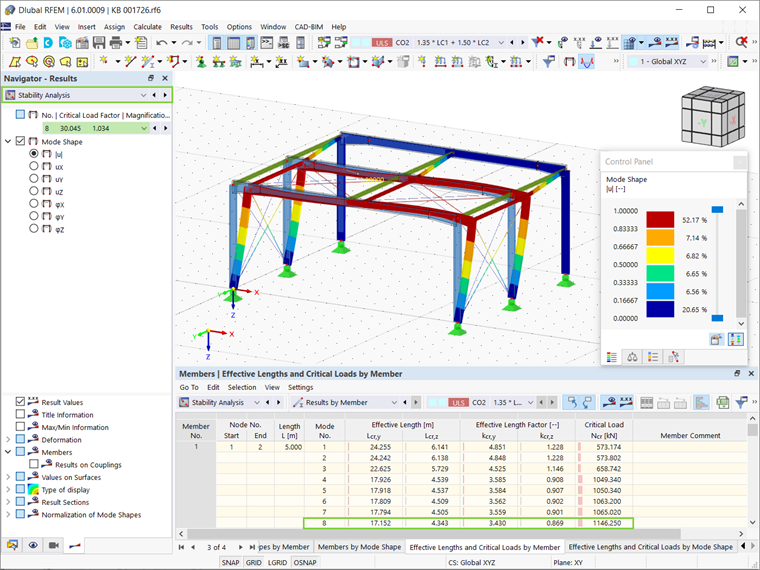
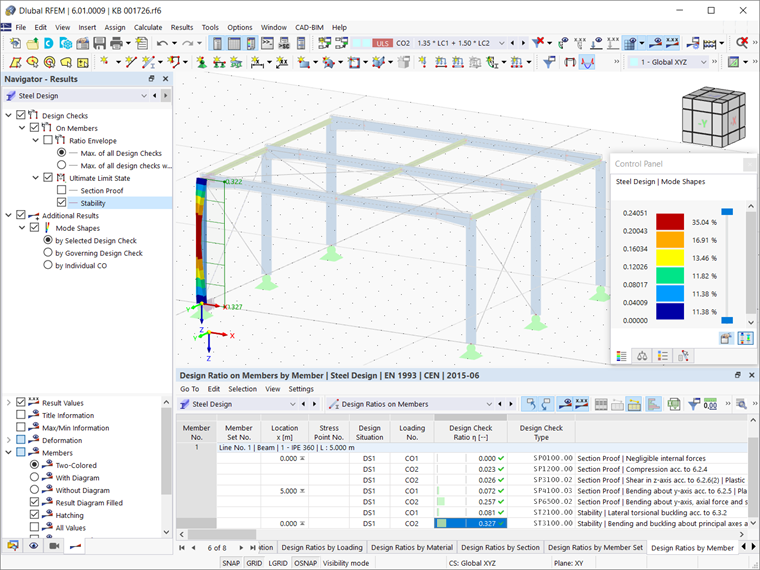
После запуска расчета, результаты отображаются как графически, так и в таблице результатов расчета на устойчивость. Свободная длина при продольном изгибе, при которой колонна выгибается в плоскости рамы, является правильной длиной для расчета соответствующего случая нагружения. В нашем примере собственной формой, представляющей потерю устойчивости при изгибе в глобальном направлении X, является собственная форма 8 (рисунок 8).
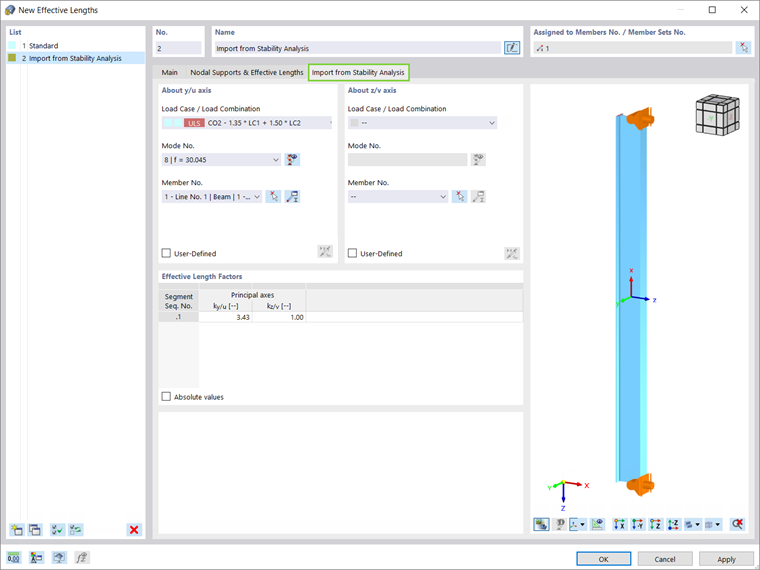
Фактически, теперь можно импортировать свободную длину из расчета на устойчивость. Когда данная опция отмечена в окне « Эффективная длина » (рисунок 9), загружение/сочетание нагрузок, собственная форма и стержень, из которого должна быть импортирована свободная длина, могут быть заданы в соответствующей вкладке. Поскольку свободная длина должна быть присвоена колонне 1, то речь идет о сочетании нагрузок 2, режиме 8 и стержне 1, соответственно (рисунок 10).
В программе RFEM 6 заданную длину можно отобразить графически, как показано на рисунке 11.
С помощью ввода настроек эффективной длины выполняется балансирование между свободной длиной при продольном изгибе и настройками свойств потери устойчивости при изгибе и кручении. При проверке опор элемент делится на сегменты для потери устойчивости при продольном изгибе. В то же время проверки опор служат для определения граничных условий для расчета критического момента потери устойчивости при продольном изгибе с кручением (Mcr ) по методу собственных значений.
Анализ устойчивости при расчете стальных конструкций
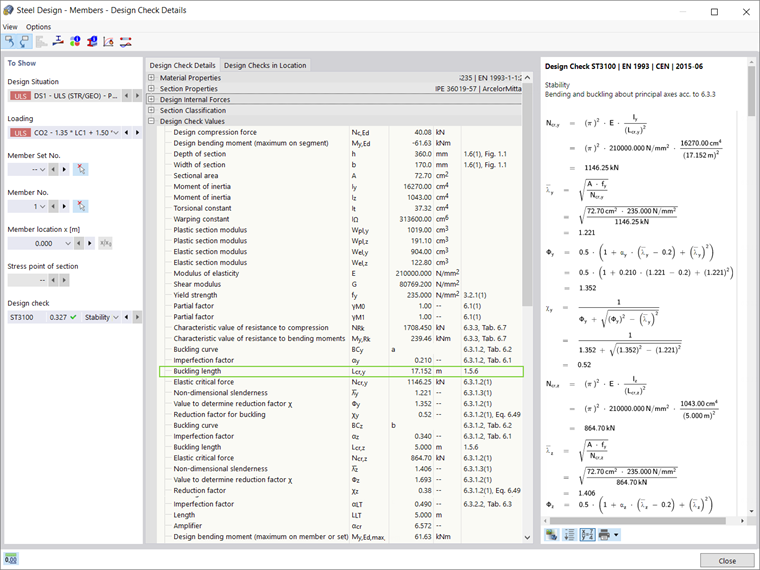
После того, как свободная длина будет присвоена соответствующему стержню, можно выполнить расчет стальной конструкции. Как показано на рисунке 12, расчеты на устойчивость отобразятся в таблице результатов. Свободная длина при продольном изгибе указана в подробностях расчета (рисунок 13). Расчет на устойчивость выполняется на основе свободной длины, полученной в анализе устойчивости.
Заключительные замечания
Свободную длину для расчета по методу замены связей в программе RFEM 6 можно определить вручную или импортировать из расчета на устойчивость. В первом случае свободная длина определяется путем присвоения узловых опор и ручной корректировки коэффициентов свободной длины в соответствии с условиями опирания стержня.
Во втором случае свободная длина является результатом расчета на устойчивость и, таким образом, может быть непосредственно присвоена стержню для расчета. Преимущество данного подхода заключается в том, что коэффициенты свободной длины и сама свободная длина рассчитываются автоматически. Это очень удобно при определенных условиях опирания, при которых в противном случае потребовался бы трудоемкий расчет вручную.
Тем не менее, при импорте из расчета на устойчивость важно получить правильную свободную длину с учетом формы потери устойчивости при изгибе и соответствующего случая нагружения.