Введение
В контексте численных моделирований ветра и валидации моделей надежность вычисленных результатов должна быть продемонстрирована посредством систематического сравнения с эталонными данными. Раздел 5.3.2 WTG-Меркблата вводит количественный метод для этой цели, используя подход доли попаданий. Этот метод предоставляет бинарную оценку для каждой точки данных, проверяя, находится ли отклонение между результатом моделирования и эталонным значением в пределах заданной абсолютной или относительной толерантности. Доля попаданий q затем вычисляется как отношение успешно валидированных точек к общему числу рассмотренных точек. Этот подход позволяет объективно и воспроизводимо оценивать качество моделирования, особенно для пространственно распределенных величин, таких как давления на поверхности или коэффициенты силы.
Определение доли попаданий
На основе раздела 5.3 WTG, в теории надежности, вероятность отказа часто определяется с использованием функции доверия, которая признает только значения 0 и 1. Аналогично, в VDI 3783-9 для моделей предсказания определяется доля попаданий q на основе числа "правильно" вычисленных значений результатов Pi в сравнении с достаточно значительными эталонными значениями Oi, как это определено ниже:
|
N |
Общее количество точек данных |
|
ni |
Индикаторная функция (1, если прогноз «правильный», в противном случае 0) |
|
Pi |
Прогнозируемое значение |
|
Oi |
Ссылка или измеренное значение |
|
Wrel |
Допустимое относительное отклонение |
|
W |
Допустимое абсолютное отклонение |
Таблица 1 (как Таблица 5.1 в WTG-Меркблате M3) определяет критерии эталона для валидации результатов коэффициентов давления в CFD моделировании. Устанавливаются максимальные допустимые отклонения (10-20%) и требуется доля попаданий более 90% для средних, среднеквадратичных и экстремальных значений. Эти пороги помогают гарантировать, что данные моделирования близко соответствуют эталонным значениям и поддерживают согласованную оценку качества.
Таблица 1: Пример критериев оценки коэффициентов силы и давления
| Рассматриваемое значение | Максимальное отклонение (W) | Доля попаданий (q) |
|---|---|---|
| Среднее значение коэффициента давления | 10% | >90% |
| Среднеквадратичное значение коэффициента давления | 20% | >90% |
| Экстремальное значение нестационарного коэффициента давления | 20% | >90% |
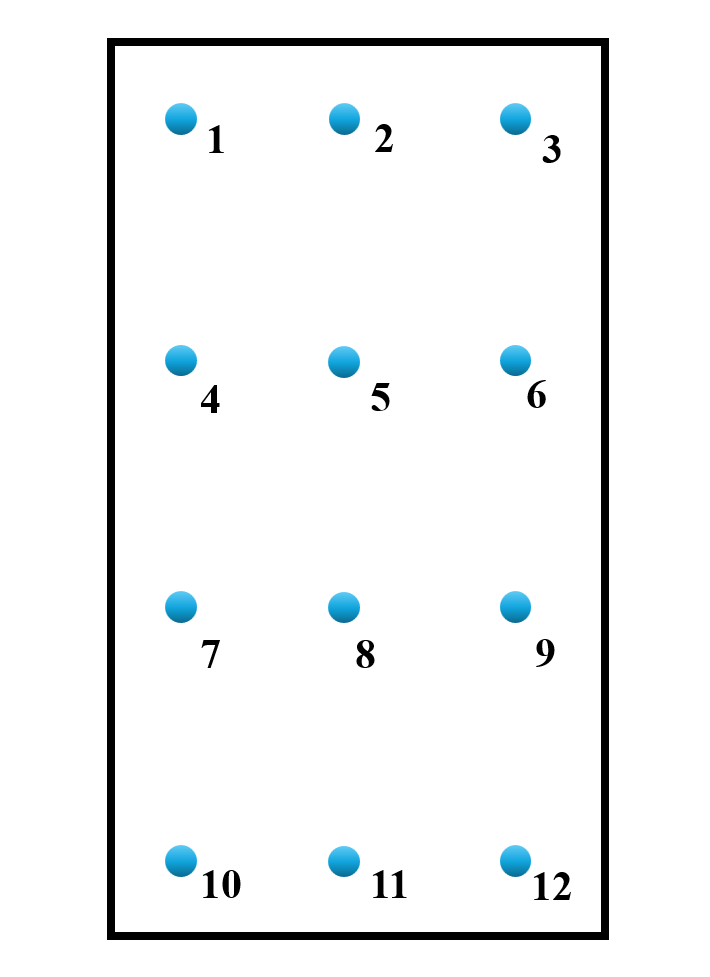
Пример: Оценка 12 измерительных точек на поверхности
Рассмотрим 12 измеренных эталонных значений Oi и соответствующих значений моделирования Pi. Мы использовали относительную толерантность отклонений W=10% для использования средних значений.
Таблица 1: Оценка доли попаданий для среднего значения 12 измерительных точек
| Точка (i) | Эталонное значение (Oi) | Смоделированное значение (Pi) | Относительное отклонение Wrel % | Доля попаданий (1 = Да, 0 = Нет) |
|---|---|---|---|---|
| 1 | 0.72 | 0.75 | 4.17 | 1 |
| 2 | 0.68 | 0.70 | 2.94 | 1 |
| 3 | 0.81 | 0.85 | 4.94 | 1 |
| 4 | 0.77 | 0.73 | 5.19 | 1 |
| 5 | 0.66 | 0.69 | 4.55 | 1 |
| 6 | 0.74 | 0.71 | 4.05 | 1 |
| 7 | 0.85 | 0.80 | 5.88 | 1 |
| 8 | 0.70 | 0.66 | 5.71 | 1 |
| 9 | 0.81 | 0.88 | 8.64 | 1 |
| 10 | 0.76 | 0.69 | 9.21 | 1 |
| 11 | 0.82 | 0.75 | 8.54 | 1 |
| 12 | 0.69 | 0.80 | 15.94 | 0 |
Доля попаданий: q=11/12≈91.7%
Она соответствует минимальному требованию (>90%) для валидации средних значений. Только точка 12 превышает толерантность (10%).
Заключение
Метод доли попаданий предлагает простой и прозрачный способ оценивать качество результатов моделирования, количественно определяя, сколько значений находится в приемлемых отклонениях от эталонных данных. Это особенно полезно для валидации коэффициентов давления и силы в моделировании ветра или аэродинамических исследованиях. Однако выбор соответствующих порогов и сегментация данных (например, по регионам или доминирующим направлениям течения) играют ключевую роль в значимой оценке.