Einführung
Im Rahmen von numerischen Windsimulationen und Modellvalidierungen muss die Zuverlässigkeit der berechneten Ergebnisse durch einen systematischen Vergleich mit Referenzdaten nachgewiesen werden. In Abschnitt 5.3.2 des WTG-Merkblatts wird hierzu eine quantitative Methode unter Verwendung des Trefferquotenansatzes vorgestellt. Mithilfe dieser Methode ist eine binäre Auswertung für jeden Datenpunkt möglich. Dabei wird überprüft, ob die Abweichung zwischen Simulationsergebnis und Referenzwert innerhalb einer definierten absoluten oder relativen Toleranz liegt. Die Trefferquote q wird dann als Verhältnis der erfolgreich validierten Punkte zur Gesamtzahl der berücksichtigten Punkte berechnet. Dieser Ansatz ermöglicht eine objektive und reproduzierbare Bewertung der Simulationsqualität, insbesondere für räumlich verteilte Größen wie Oberflächendrücke oder Kraftkoeffizienten.
Definition der Trefferquote
Basierend auf WTG-Abschnitt 5.3 wird im Bereich der Zuverlässigkeitstheorie die Ausfallwahrscheinlichkeit häufig mithilfe einer Konfidenzfunktion bestimmt, die nur die Werte 0 und 1 annimmt. Analog dazu wird in VDI 3783-9 eine Trefferquote q für Vorhersagemodelle definiert, die sich auf die Anzahl der "korrekt" berechneten Ergebniswerte Pi bezieht, wobei diese mit den ausreichend signifikanten Referenzwerten Oi verglichen werden.
|
N |
Gesamtzahl der Datenpunkte |
|
ni |
Indikatorfunktion (1 bei „korrekter“ Vorhersage, sonst 0) |
|
Pi |
Vorhersagewert |
|
Oi |
Referenz- oder Messwert |
|
Wrel |
Zulässige relative Abweichung |
|
W |
Zulässige absolute Abweichung |
In Tabelle 1 (wie Tabelle 5.1 im WTG-Merkblatt M3) sind Benchmark-Kriterien zur Validierung von Druckkoeffizientenergebnissen in CFD-Simulationen definiert. Sie legt maximal zulässige Abweichungen von 10–20 % fest und erfordert eine Trefferquote von über 90 % für Mittelwert, RMS und Extremwerte. Diese Schwellenwerte tragen dazu bei, dass die Simulationsdaten eng mit den Referenzwerten übereinstimmen, und ermöglichen eine konsistente Qualitätsbewertung.
Tabelle 1: Beispielhafte Bewertungskriterien für Kraft- und Druckkoeffizienten
| Betrachteter Wert | Maximale Abweichung (W) | Trefferquote (q) |
|---|---|---|
| Mittelwert des Druckkoeffizienten | 10% | >90% |
| RMS-Wert des Druckkoeffizienten | 20% | >90% |
| Extremwert des instationären Druckkoeffizienten | 20% | >90% |
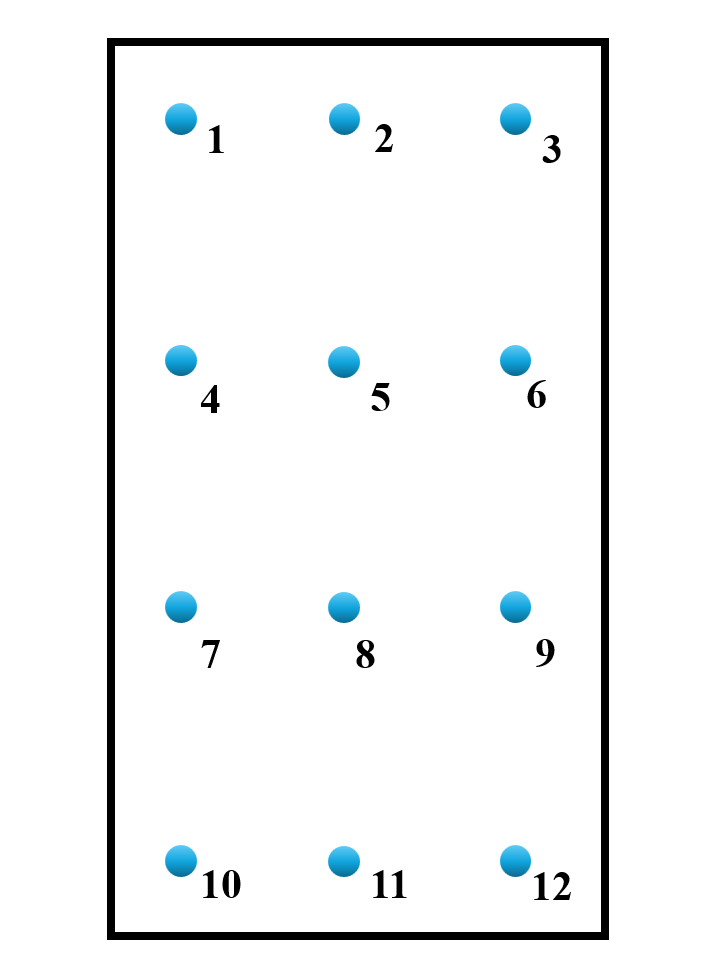
Beispiel: Bewertung von 12 Messpunkten auf einer Oberfläche
Betrachten wir 12 gemessene Referenzwerte Oi und die entsprechenden Simulationswerte Pi. Für die Verwendung von Durchschnittswerten haben wir die relative Abweichungstoleranz von W=10 % verwendet.
Tabelle 1: Bewertung der Trefferquote für den Mittelwert von 12 Messpunkten.
| Punkt (i) | Referenzwert (Oi) | Simulierter Wert (Pi) | Relative Abweichung Wrel % | Trefferquote (1 = Ja, 0 = Nein) |
|---|---|---|---|---|
| 1 | 0.72 | 0.75 | 4.17 | 1 |
| 2 | 0.68 | 0.70 | 2.94 | 1 |
| 3 | 0.81 | 0.85 | 4.94 | 1 |
| 4 | 0.77 | 0.73 | 5.19 | 1 |
| 5 | 0.66 | 0.69 | 4.55 | 1 |
| 6 | 0.74 | 0.71 | 4.05 | 1 |
| 7 | 0.85 | 0.80 | 5.88 | 1 |
| 8 | 0.70 | 0.66 | 5.71 | 1 |
| 9 | 0.81 | 0.88 | 8.64 | 1 |
| 10 | 0.76 | 0.69 | 9.21 | 1 |
| 11 | 0.82 | 0.75 | 8.54 | 1 |
| 12 | 0.69 | 0.80 | 15.94 | 0 |
Trefferquote : q=11/12≈91,7%
Die Mindestanforderung (>90 %) zur Validierung von Mittelwerten wird erfüllt. Lediglich Punkt 12 überschreitet die Toleranz von 10 %.
Fazit
Die Hit-Rate-Methode ist eine einfache und transparente Möglichkeit, die Qualität von Simulationsergebnissen zu beurteilen. Dabei wird quantifiziert, wie viele Werte innerhalb akzeptabler Abweichungen von Referenzdaten liegen. Sie ist besonders nützlich für die Validierung von Druck- und Kraftkoeffizienten in Windsimulationen oder aerodynamischen Studien. Für eine aussagekräftige Bewertung sind jedoch die Auswahl geeigneter Schwellenwerte und die Segmentierung der Daten (z. B. nach Regionen oder dominanter Strömungsrichtung) entscheidend.