11608x

001601

Dipl.-Ing. (FH) Alexander Meierhofer

2019-11-04

Определение характеристик материала сталефибробетона и его применение в программе RFEM

Сталефибробетон в настоящее время применяется в основном для изготовления полов промышленно-складских зданий, фундаментных плит с небольшими нагрузками, стен подвалов и цокольных этажей. С момента публикации в 2010 году первого руководства Немецкого комитета по железобетону (DAfStb) по сталефибробетону, инженеры-строители могут использовать нормативы для проектирования сталефибробетона. Фибробетон становится все более популярным в строительстве. В данной статье описываются отдельные параметры материала сталефибробетона, а также определенные способы работы с данными параметрами материала в программе для расчета по МКЭ - RFEM.

свойства материала

По норме DIN EN 206-1, фибробетон - это бетон, в который добавляется стальное волокно для достижения определенных свойств. При добавлении достаточного количества стальных волокон бетон может передавать растягивающие силы даже в случае образования трещины. На рисунке 01 показано сравнение общих свойств неармированного бетона и сталефибробетона при растяжении. Мы видим, что сопротивление растяжению сталефибробетона уменьшается с увеличением деформации, а кривая нагрузка-деформация имеет нисходящую ветвь после достижения предела прочности при растяжении.

1 Нагрузочно-деформационное поведение а) неармированного бетона и б) стального фибробетона

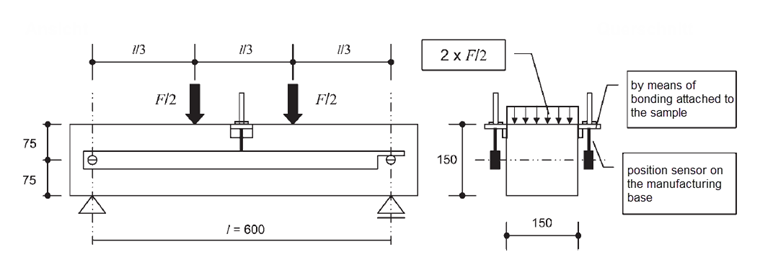
Прочность сталефибробетонного композитного материала после превышения прочности бетона на растяжение называется прочностью на растяжение после растрескивания. Растягивающие силы, фактически возникающие в стальных волокнах, относятся к поверхности растянутой зоны бетона. Прочность на растяжение после растрескивания обычно определяется в лаборатории строительной механики с помощью испытания на растяжение при изгибе по {%://#Refer [1]]]. В качестве образцов для испытаний используются балки размером b/h/l = 150 мм/150 мм/700 мм. Поскольку для рабочей кривой сталефибробетона важно поведение при изгибе с растяжением в области после растрескивания, то испытание на изгиб в 4 точках выполняется с контролируемым перемещением. На рисунке 02 показано графическое отображение размеров для 4-точечного испытания на изгиб.

2 Prüfeinrichtung zur Ermittlung der Nachrissbiegezugfestigkeit (Abmessungen in mm)

Из-за экспериментальной природы испытания на изгиб в 4 точках, область растрескивания может находится в любом месте на образце балки, так как локальная нагрузка между двумя точками нагружения постоянна. Как показано далее на рисунке, после законченного эксперимента (давление увеличивалось вручную после окончания эксперимента для расширения трещин) трещина образуется произвольно между двумя прижимными роликами в решающей точке (= самая слабая область).

3 Завершено испытание на 4-точечный изгиб с раскрытием трещин (Изображение: BPL Müller and Lobisch GmbH)

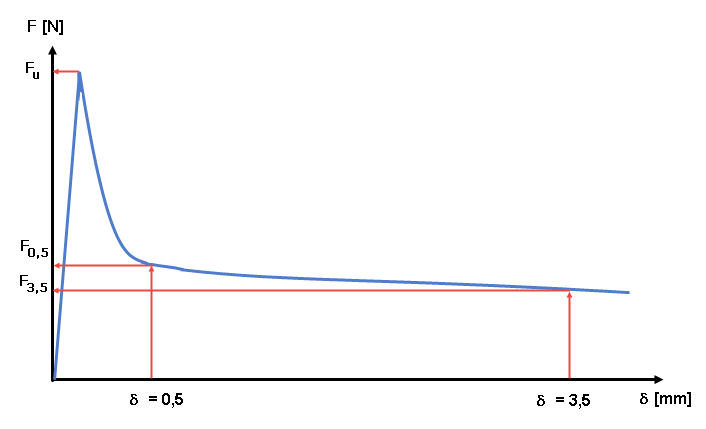
Результаты испытания отображены на кривой зависимости деформации от нагрузки (см. рисунок 04). По данной кривой нагрузка-деформация определяет эквивалентную прочность на растяжение и, с помощью коэффициентов преобразования, прочность на растяжение после растрескивания сталефибробетона. Различают характеристическое значение для оценки предельного состояния по пригодности к эксплуатации (= малые деформации, δ = 0,5 мм) и определяющий параметр предельного состояния по несущей способности (= большие деформации, δ = 3,5 мм).

4 Символическая кривая нагрузка-деформация для определения прочности на растяжение после растрескивания

Прочность сталефибробетона на растяжение при изгибе после растрескивания определяется из значений нагрузок F_0,5 при δ = 0,5 мм и F_3,5 при δ = 3,5 мм. В данном случае полученную нагрузку L_i (с i=0,5 или 3,5) нужно умножить на соответствующее плечо нагрузки и разделить на момент сопротивления W_j сечения без трещин. Среднее значение прочности на растяжение при изгибе после растрескивания f^f_cflm,Li для ряда n испытательных балок рассчитывается как среднее арифметическое отдельных значений прочности на растяжение после растрескивания.

{f^{f}}_{cflm, Li} = \frac{1}{n} \sum_{j = 1}^{n} {f^{f}}_{cflm, Li, j} = \frac{1}{n} \sum_{j = 1}^{n} \frac{M_{Li, j}}{W_{j}} = \frac{1}{n} \sum_{j = 1}^{n} \frac{F_{Li, j} \cdot l_{j}}{b_{j} \cdot {h^{2}}_{j}}

Средняя прочность на растяжение при изгибе после растрескивания

Классификация сталефибробетонного композитного материала в соответствии с немецким руководством по сталефибробетону DAfStb предусматривает два различных класса исполнения: L1 и L2. Класс исполнения L1 описывает свойства материала при небольших деформациях (δ = 0,5 мм), а класс исполнения L2 - поведение при больших деформациях (δ = 3,5 мм). Обозначение класса исполнения Li соответствует характеристическому значению прочности на растяжение при изгибе после растрескивания f^f_cflk,Li в Н/мм² при соответствующих деформациях. Характеристическая прочность на растяжение при изгибе после растрескивания рассчитывается из средней прочности на растяжение при изгибе после растрескивания^ff_cflm,Li по [1] следующим образом.

{f^{f}}_{cflk, Li} = e^{({Lf}^{f}_{cflm, Li} - k_{s} \cdot L_{s})} \leq 0.51 \cdot {f^{f}}_{cflm, Li}

Lf^f_cflm,Li	среднее значение логарифмированных результатов отдельных испытаний f^f_cfl,Li,j (подробности см. в [1])
L_s	стандартное отклонение логарифмированных результатов отдельных испытаний (подробности см. в [1])
k_s	поправочный коэффициент квантиля для неизвестных стандартных отклонений для 5% квантиля с 75%-ным доверительным интервалом (подробности смотри [1])

Нормативная прочность на растяжение при изгибе после растрескивания

Таким образом, описание сталефибробетона осуществляется путем добавления буквы L, обозначающей класс исполнения с характерной прочностью на растяжение при изгибе после растрескивания для деформаций 1 (ПС 2г) и 2 (ПС 1г). Например, сталефибробетон C30/37 L0.9/L0.6 XC1 имеет характеристическую прочность на растяжение при изгибе после растрескивания, равную 0,9 Н/мм² при деформации 1 и 0,6 Н/мм² при деформации 2.

Кривая напряжения сталефибробетона

Кривые зависимости деформаций от напряжения необходимы для расчета конструктивных элементов из сталефибробетона. Для этого характеристическое значение прочности на растяжение при изгибе после растрескивания f^f_cflk,Li, описанное выше, преобразуется с помощью коэффициентов β в прочность при осевом растяжении после растрескивания f^f_ct0,i согласно {%><#Refer [1]]]. В таблице R3 руководства Немецкого комитета по железобетону (DAfStb) по сталефибробетону {%://#Refer [1]]] уже указаны основные значения прочности при осевом растяжении после растрескивания f^f_{ct0, i} для соответствующих классов исполнения (см.рисунок 05).

5 Gebräuchlichste Leistungsklassen L1 und L2 mit zugehörigen Grundwerten der zentrischen Nachrisszugfestigkeit

Чтобы получить расчетные значения f^f_ctR,i для кривой зависимости деформаций от напряжения, мы должны преобразовать основные значения прочности при осевом растяжении после растрескивания с помощью двух поправочных коэффициентов κ^f_G и κ^f_F.

{f^{f}}_{ctR, i} = {κ^{f}}_{G} \cdot {κ^{f}}_{F} \cdot {f^{f}}_{ct 0, i}

κ^f_G	коэффициент учета влияния размера конструктивного элемента на вариационный коэффициент = 1,0 + A^f_ct ⋅ 0,5 < 1,70
A_ct	Площадь сечения, подверженная растягивающему напряжению зон с трещинами в м², приходящихся на соответствующее состояние равновесия
κ^f_F	коэффициент учета ориентации волокон = 0,5. У плоскостных, изготовленных в горизонтальной плоскости пластинчатых конструктивных элементов (b < 5) допускается допущение κ^f_F = 1,0 при изгибающем и растягивающем напряжении.

Вычисленное значение для кривой напряжения-деформации

Директива по сталефиброматериалам [1] предполагает, что деформация 1 при δ = 0,5 мм в 4-точечном испытании на изгиб соответствует растяжению ε = 0,0035, а деформация 2 при δ = 3,5 мм будет соответствуют деформации ε = 0,025.

В зависимости от метода расчета в {%ref#Refer [1]]] приведены различные диаграммы напряжения-деформации в области растяжения. В нелинейном расчете деформаций и внутренних сил, в области растяжения применяется полилинейное соотношение, показанное на рисунке 06. Линейное распределение можно применить до достижения предела прочности бетона при растяжении f_ctm. Согласно {%ref#Refer [1]]], диаграмма напряжения, показанная синим цветом на рисунке 06, может использоваться только у сталефибробетона с соотношением L2/L1 ≥ 0,7. Если соотношение классов исполнения L2/L1 ≤ 0,7, то можно применить только распределение напряжений (зеленая пунктирная линия на рисунке 06).

6 Spannungs-Dehnungs-Linie im Zugbereich nach [1] für die Schnittgrößen- und Verformungsermittlung bei nichtlinearen Verfahren

При расчете сечения на предельное состояние по несущей способности нельзя использовать прочность бетона на растяжение f_ctm. Дополнительная прочность на растяжение, которую можно применить в данном случае, является следствием действия исключительно растягивающей силы, передаваемой через стальные волокна в трещине. Кроме того, необходимо применять прочности на растяжение для расчета предельной несущей способности, с расчетными значениями f^f_ctd,Li. Данные значения получают путем умножения расчетных значений f^f_ctR,Li на коэффициент уменьшения α^f_c и деления на частный коэффициент надежности γ^f_ct. Применение f^f_ctd,L1 и f^f_{ctd, L2} (синяя сплошная линия на рисунке 07) ограничено случаями, когда соотношение L2/L1 ≥ 0,7. Распределение напряжения, показанное на рисунке 07 зеленой пунктирной линией, можно упрощенно применить при соотношении L2/L1 ≤ 1.

7 Spannungs-Dehnungs-Linie auf der Zugseite gemäß [1] für die Querschnittsbemessung im Grenzzustand der Tragfähigkeit

В области сжатия кривой зависимости деформаций от напряжения сталефибробетона нет никаких различий между обычным бетоном без волокон и сталефибробетоном. Соотношение деформаций и напряжения в области сжатия неизменно регулируется предписанием EN 1992-1-1 {%ref#Refer [4]]]. Поэтому для нелинейного расчета деформаций и внутренних напряжений рекомендуется использовать диаграмму параболы по разделу 3.1.5 [4] (см. рисунок 08 a) или прямоугольник параболы по разделу 3.1.6 сил [4] для определения соотношения напряжения-деформации в области сжатия.

8 Spannungs-Dehnungs-Linie nach [4] für den Druckbereich: a) für die nichtlineare Berechnung; b) für die Querschnittsbemessung

Нелинейный расчет с помощью программы RFEM

Согласно {%ref#Refer [1]]], нелинейные методы расчета в целом могут применяться у конструктивных элементов из сталефибробетона, в случае, если основная несущая способность достигается с помощью арматурной стали. Во всех других случаях нелинейный расчет можно применять только для конструктивных элементов с упругим основанием, заанкерованных подводных бетонных опор, плит основания на сваях, конструктивных элементов в форме оболочки и монолитных контейнеров промышленного изготовления.

В следующей статье мы зададим в программе RFEM кривую зависимости деформаций от напряжения у сталефибробетона и проверим свойства материала. Для целей нашей статьи сделаем это сначала только у конечного элемента с одноосной нагрузкой на растяжение. С помощью этого простого примера мы проверим модель материала, используемую в RFEM, на поглощение одноосной нагрузки на растяжение.

Для нелинейного расчета внутренних сил и деформаций сталефибробетона, применяется в области сжатия диаграмма напряжения-деформации, которая представляет собой параболу согласно 3.1.5 EN 1992-1-1 {%://#Refer [4] ]]], так и в области растяжения полилинейного распределения с учетом прочности бетона на растяжение f_ctm (рисунок 06). В программе RFEM необходимо применить модель материала, которая отражает нисходящую ветвь кривой после образования трещины. С помощью дополнительного модуля RF-MAT NL в RFEM можно точно отобразить данное свойство в модели материала "изотропное повреждение" 2D/3D.

Модель материала "Изотропное повреждение" была подробно описана в одной из предыдущих статей:
KB 001461 │ Нелинейное повреждение модели материала

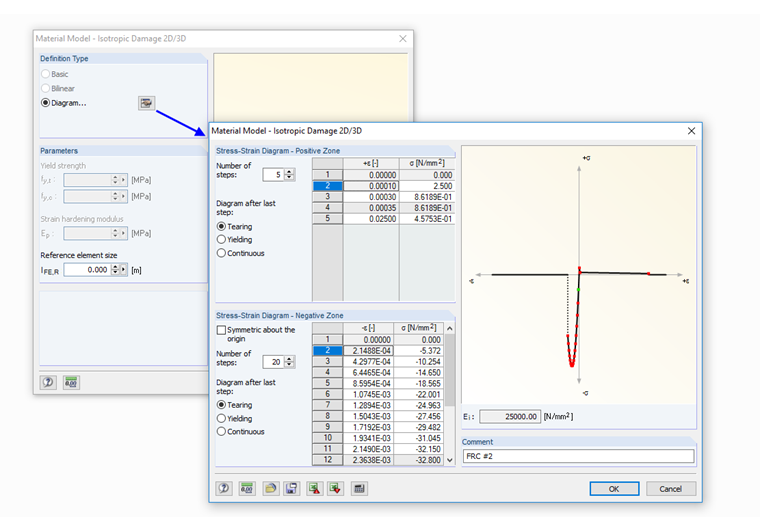
Кривая напряжения-деформации обычно задается в RFEM. Область сжатия и растяжения можно задать индивидуально с помощью опции «Диаграмма ...». Только модуль упругости в начале должен быть идентичным соответствующим последующим точкам в области сжатия и растяжения. Размер контрольного элемента l_FE,R оставлен без изменений, длиной 0,0 м. Таким образом можно гарантировать, что заданная кривая напряжения будет в расчете применена в области повреждения 1: 1. На рисунке 09 показан ввод данных в диалоговом окне RFEM для расчета сталефибробетона.

9 Definition der Spannungs-Dehnungs-Linie des Stahlfaserbetons

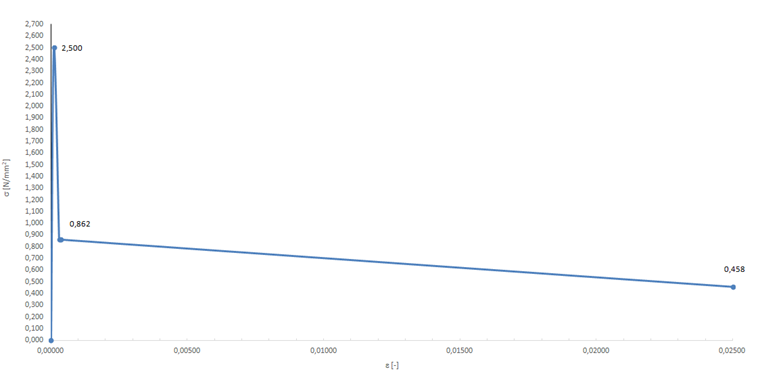
Так как показанные свойства при растяжении после образования трещин необходимо проанализировать более основательно, то характеристики в области растяжения тестируемого сталефибробетона далее описаны более подробно:

f_ctm = 2500 Н/мм²
1,04 ⋅ f^f_ctr,L1 = 0,862 Н/мм²
1,04 ⋅ f^f_ctr,L2 = 0,458 Н/мм²

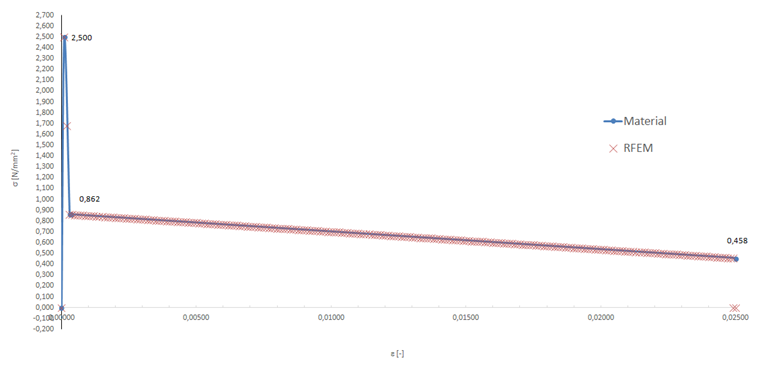
На основе упомянутых характеристик материала получается кривая зависимости деформаций от напряжения в области растяжения, показанная на рисунке 10.

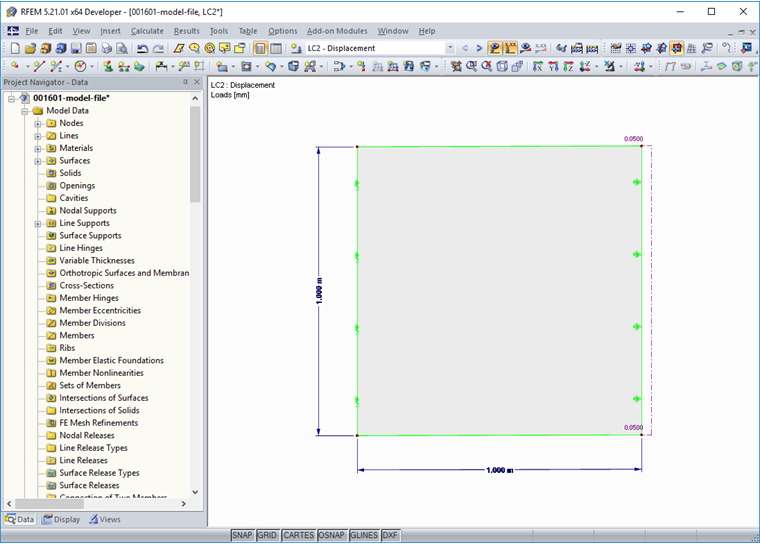
Berechnungsmodell in RFEM: ein FE-Element, links gehalten, rechts gezogen

10 Расчетная модель в программе RFEM: ein FE-Element, links gehalten, rechts gezogen

Для того, чтобы избежать влияния соседних элементов и двухосного напряженного состояния на результаты анализа, проверим материал на конечном элементе с длиной сторон 1 ⋅ 1 м. Элемент удерживается горизонтально на одной стороне элемента, а затем вытягивается на противоположной стороне. Для получения изображения прочности на растяжение после образования трещин необходимо применить нагружение с измерением перемещений, тем же способом, как описано выше в 4х-точечном испытании на изгиб. На рисунке 11 показана модель для расчета в программе RFEM.

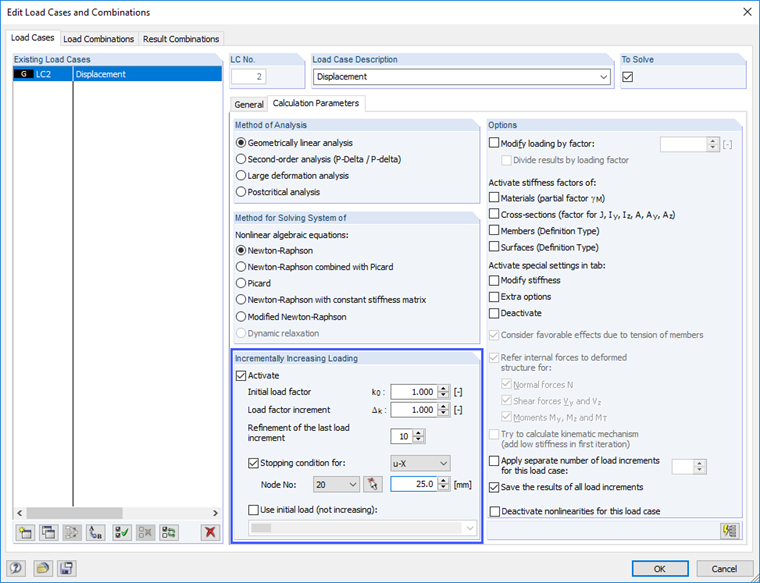
11 Vorgabe der stufenweise ansteigenden Belastung

С помощью функции «Постепенное приращение нагрузки» в параметрах расчета нагружения деформация будет увеличиваться до достижения критерия разрыва. В качестве критерия разрыва задано смещение узла, равное 25,1 мм, что соответствует деформации ε 0,0251.

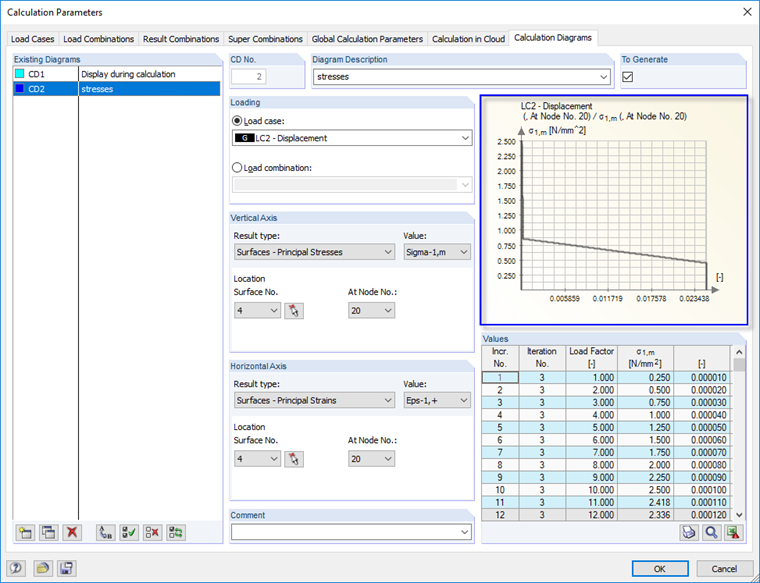
12 Darstellung der 1. Membranspannung im Berechnungsdiagramm

Для оценки результатов расчета используется мембранное напряжение в направлении первой главной оси σ_1,m. В диалоговом окне «Параметры расчета» мы можем отобразить график результатов расчета при поэтапном приращении нагрузки.

13 Gegenüberstellung der RFEM-Ergebnisse mit definierter Materialeigenschaft im Zugbereich

Полученное мембранное напряжение точно соответствует заданному распределению прочности на растяжение после образования трещин. На последующей диаграмме основное напряжение σ_1,m определено на основе кривой зависимости деформаций от напряжения в области растяжения сталефибробетона. Результаты, рассчитанные в RFEM, точно соответствуют заданной рабочей диаграмме.

14 Spannungs-Dehnungs-Linie des Stahlfaserbetons im Zugbereich für eine nichtlineare Berechnung

Заключение

Используя модель материала "изотропное повреждение 2D/3D" мы можем точно проверить свойства сталефибробетона после образования трещин при нагружении одноосной растягивающей нагрузкой. Необходимо обратить внимание на то, что в подобных проверочных расчетах нужно исключить любое влияние соседних элементов, многоосных напряженных состояний или модификаций в модели материала, что можно сделать с помощью задания размера проверочного элемента l_FE,R.

База знаний

KB 001601 | Определение характеристик сталефибробетона и его применение в программе RFEM

База знаний

KB 001601 | Определение характеристик сталефибробетона и его применение в программе RFEM

Автор

Г-н Мейергофер является руководителем отдела разработки программ для расчета железобетонных конструкций.

Ссылки

Программы для расчета железобетонных конструкций

Ссылки

CEN (2000). Бетон - Часть 1: Festlegung, Eigenschaften, Herstellung und Konformität; EN 206-1:2000
Немецкий комитет по строительному бетону (DAfStb). (2012). Железобетон - оборудование и условия DIN EN 1992-1-1 в соединении с DIN EN 1992-1-1/NA, DIN EN 206-1 в соединении с DIN 1045-2 и DIN EN 13670 в соединении DIN 1045-3; DAfStb Stahlfaserbeton:2012-11.
Teutsch, M., Wins, U., & Alfes, C: Stahlfaserbeton nach DAfStb-Richtlinie "Stahlfaserbeton", Beton- und Stahlbetonbau 105, Seiten 539 - 551. Берлин: Ernst & Sohn, 2010
Европейский комитет по стандартизации (CEN). Расчет железобетонных конструкций - Часть 1-1: Общие правила и правила для надземных сооружений, EN 1993-1-1:2005. Берлин: Beuth VerLAG GmbH.
Dlubal Software, сентябрь 2017 (2018). Руководство пользователя RFEM. Тифенбах,

Скачивания

Файл модели в программе RFEM

392 KB

;