Stanovení materiálových vlastností drátkobetonu a jeho použití v programu RFEM

Materiálové charakteristiky

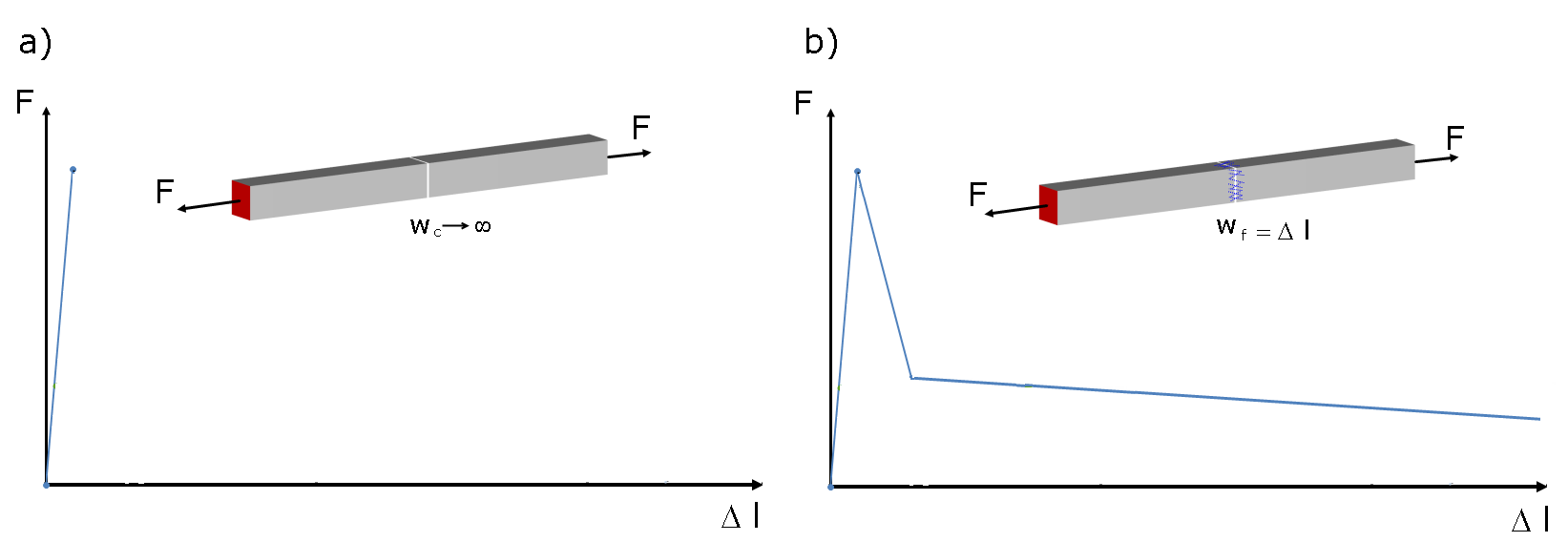
V případě vláknobetonu se podle DIN EN 206-1 jedná o beton, do něhož se k dosažení určitých vlastností přidávají ocelová vlákna. Při přidání dostatečného množství ocelových vláken je beton schopen odolávat tahovému napětí i po vzniku trhliny. Na obr. 01 je znázorněno obecné chování nevyztuženého betonu a betonu vyztuženého ocelovými vlákny při působení tahu. Vidíme, že tahová únosnost drátkobetonu klesá se zvyšující se deformací; křivka vztahu mezi zatížením a deformací vykazuje po dosažení pevnosti v tahu pokles.

Vztah zatížení a deformace a) nevyztuženého betonu a b) drátkobetonu

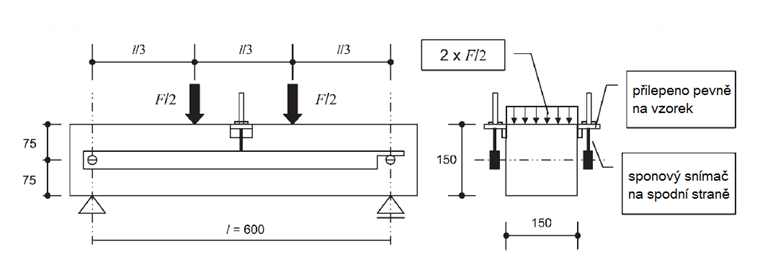
Pevnost kompozitního materiálu, jakým je drátkobeton, se po překročení pevnosti betonu v tahu nazývá pevnost v tahu po vzniku trhliny. Přitom jsou tahové síly v ocelových vláknech vztaženy na plochu tahové oblasti betonu. Pevnost v tahu po vzniku trhliny se zpravidla určuje v laboratoři pomocí tahové zkoušky za ohybu podle [1]. Jako zkušební tělesa se přitom používají nosníky o rozměrech b/h/l = 150 mm/150 mm/700 mm. Vzhledem k tomu, že pro pracovní diagram drátkobetonu je důležité chování v tahu za ohybu v oblasti porušené trhlinou, provádí se čtyřbodová ohybová zkouška. Na obr. 02 je znázorněna čtyřbodová ohybová zkouška se zakreslením rozměrů.

Prüfeinrichtung zur Ermittlung der Nachrissbiegezugfestigkeit (Abmessungen in mm)

Protože se v případě této čtyřbodové ohybové zkoušky jedná o experiment, může se místo vzniku trhliny nacházet na zkušebním nosníku na libovolném místě - lokální namáhání mezi oběma působišti zatížení je totiž konstantní. Na obrázku níže lze po ukončeném pokusu pozorovat (tlak byl po ukončení experimentu ještě vyvíjen dál ručně pro zvětšení trhliny), že trhlina se vytvoří volně mezi oběma válci na rozhodujícím (nejslabším) místě.

Dokončená čtyřbodová ohybová zkouška s trhlinou (obrázek: BPL Müller a Lobisch GmbH)

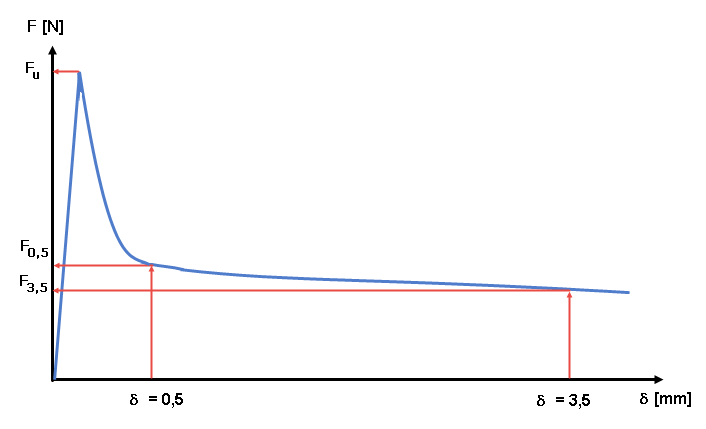
Výsledky zkoušky zaznamenává křivka vztahu mezi zatížením a deformací (viz obr. 04). Z této křivky se stanoví takzvané ekvivalentní pevnosti v tahu za ohybu a dále pomocí převodních součinitelů pevnost drátkobetonu v tahu po vzniku trhliny. Rozlišujeme přitom mezi charakteristickou hodnotou pro posouzení mezního stavu použitelnosti (= malé deformace, δ = 0,5 mm) a rozhodujícím parametrem pro mezní stav únosnosti (= velké deformace, δ = 3,5 mm).

Symbolická křivka vztahu mezi zatížením a deformací pro stanovení pevnosti v tahu po vzniku trhliny

Pevnosti drátkobetonu v tahu za ohybu po vzniku trhliny se stanoví na základě hodnot zatížení F_0,5 při δ = 0,5 mm a F_3,5 při δ = 3,5 mm. Dosažené zatížení L_i (s i=0,5, respektive 3,5) se přitom vynásobí příslušným ramenem zatížení a vydělí momentem únosnosti W _j neporušeného průřezu. Průměrná hodnota pevnosti v tahu za ohybu po vzniku trhliny f^f_cflm,Li se stanoví u testovací řady n zkušebních nosníků jako aritmetický průměr jednotlivých hodnot pevnosti v tahu po vzniku trhliny.

Pro klasifikaci drátkobetonu jakožto kompozitního materiálu stanoví příslušná německá směrnice DAfStb dvě různé výkonnostní třídy L1 a L2. Výkonnostní třída L1 udává materiálové charakteristiky při malých deformacích (δ = 0,5 mm) a výkonnostní třída L2 pak chování při větších deformacích (δ = 3,5 mm). Označení výkonnostních tříd Li odpovídá charakteristické hodnotě pevnosti v tahu za ohybu po vzniku trhliny f^f_cflk,Li v N/mm² pro příslušné deformace. Charakteristická pevnost v tahu za ohybu po vzniku trhliny se podle [1] stanoví tak, jak uvádíme níže, na základě průměrné pevnosti v tahu za ohybu po vzniku trhliny f^f_cflm,Li.

kde
Lf^f_cflm,Li ... průměrná hodnota logaritmovaných výsledků jednotlivých zkoušek f^f_cfl,Li,j (pro podrobnosti viz [1])
L_s ... standardní odchylka logaritmovaných výsledků jednotlivých zkoušek (pro podrobnosti viz [1]
k_s ... opravný součinitel pro neznámé standardní odchylky pro 5% kvantil s 75% mírou pravděpodobnosti (pro podrobnosti viz [1])

Označení drátkobetonu je tak doplněno písmenem L pro výkonnostní třídu s charakteristickou pevností v tahu za ohybu po vzniku trhliny pro deformace 1 (MSP) a 2 (MSÚ). Drátkobeton C30/37 L0,9/ L0,6 XC1 tak má například charakteristickou pevnost v tahu za ohybu po vzniku trhliny 0,9 N/mm² pro deformaci 1 a 0,6 N/mm² pro deformaci 2.

Pracovní diagram drátkobetonu

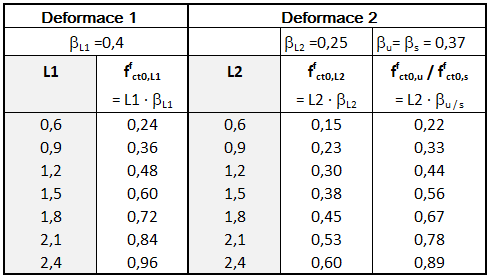
Pro posouzení konstrukčních prvků z drátkobetonu jsou zapotřebí pracovní diagramy. Výše uvedené charakteristické pevnosti v tahu za ohybu po vzniku trhliny f^f_cflk,Li se tak pomocí součinitelů β přepočítají na pevnosti v dostředném tahu po vzniku trhliny f^f_ct0,i podle [1]. V tabulce R3 [1] směrnice výboru DAfStb ke kompozitnímu materiálu [1] jsou již uvedeny základní hodnoty pevnosti v dostředném tahu po vzniku trhliny f^f_ct0,i pro příslušné výkonnostní třídy (viz obr. 05).

Gebräuchlichste Leistungsklassen L1 und L2 mit zugehörigen Grundwerten der zentrischen Nachrisszugfestigkeit

Abychom získali výpočtové hodnoty f^f_ctR,i pro pracovní diagram, je třeba základní hodnoty pevnosti v dostředném tahu po vzniku trhliny ještě upravit dvěma opravnými součiniteli κ^f_G a κ^f_F.

f^f_ctR,i = κ^f_G ⋅ κ^f_F ⋅ f^f_ct0,i

kde
κ^f_G ... součinitel pro zohlednění vlivu velikosti dílce na variační součinitel = 1,0 + A^f_ct ⋅ 0,5 < 1,70
A_ct ... průřezová plocha oblastí porušených trhlinami v m², na kterou působí tahové napětí a která náleží k příslušnému stavu rovnováhy
κ^f_F ... součinitel zohledňující orientaci vláken = 0,5. U rovinných, ve vodorovné poloze vyrobených plošných konstrukčních prvků (b <5) lze uvažovat κ^f_F = 1,0 při namáhání v tahu za ohybu.

Směrnice ke kompozitnímu materiálu [1] vychází z předpokladu, že deformace 1 s δ = 0,5 mm při čtyřbodové ohybové zkoušce odpovídá přetvoření ε = 0,0035 a deformace 2 s δ = 3,5 mm přetvoření ε = 0,025.

V závislosti na zvoleném výpočtu jsou v [1] k dispozici pro oblast tahu různé pracovní diagramy. Při nelineárním výpočtu deformací a vnitřních sil se v tahové oblasti uplatňuje multilineární vztah znázorněný na obr. 06. Lineární průběh lze přitom aplikovat až do dosažení pevnosti betonu v tahu f_ctm. Pracovní diagram znázorněný modře na obr. 06 je podle [1] přípustný pouze u drátkobetonu s poměrem L2 / L1 ≥ 0,7. Pokud je poměr výkonnostních tříd L2/L1 ≤ 0,7, lze použít pouze rozdělení napětí (zelená čárkovaná linie na obr. 06).

Spannungs-Dehnungs-Linie im Zugbereich nach [1] für die Schnittgrößen- und Verformungsermittlung bei nichtlinearen Verfahren

Pro posouzení průřezu v mezním stavu únosnosti nelze použít pevnost betonu v tahu f_ctm. Přídavná pevnost v tahu, kterou lze použít, plyne pouze z tahové síly přenášené ocelovými vlákny v trhlině. Dále je třeba uvažovat pevnosti v tahu pro posouzení únosnosti s návrhovými hodnotami f^f_ctd,Li. Získají se vynásobením výpočtových hodnot f^f_ctR,Li redukčním součinitelem α^f_c a vydělením dílčím součinitelem spolehlivosti γ^f_ct. Použití f^f_ctd,L1 a f^f_ctd,L2 (modrá plná čára na obr. 07) je omezeno na případy, kdy je poměr L2 / L1 ≥ 0,7. Rozdělení napětí, které je vyznačeno na obr. 07 zelenou čárkovanou linií, se může zjednodušeně použít v případě poměru L2/L1 ≤ 1.

Spannungs-Dehnungs-Linie auf der Zugseite gemäß [1] für die Querschnittsbemessung im Grenzzustand der Tragfähigkeit

V tlačené oblasti pracovního diagramu není žádný rozdíl mezi betonem bez vláken a betonem vyztuženým ocelovými vlákny. Pro vztah mezi napětím a přetvořením v tlačené oblasti platí beze změny ustanovení EN 1992-1-1 [4]. Pro nelineární výpočet deformace a vnitřních sil se tak použije parabolický pracovní diagram podle čl. 3.1.5 [4] (viz obr. 08 a), respektive pro návrh průřezu parabolicko-rektangulární pracovní diagram podle čl. 3.1.6 [4] pro beton namáhaný tlakem.

Spannungs-Dehnungs-Linie nach [4] für den Druckbereich: a) für die nichtlineare Berechnung; b) für die Querschnittsbemessung

Nelineární výpočet v programu RFEM

Nelineární metodu lze podle [1] používat v zásadě u konstrukčních prvků z drátkobetonu, pokud je únosnost převážně dosažena použitím betonářské výztuže. Ve všech ostatních případech lze nelineární výpočet uplatnit pouze u konstrukčních prvků s pružným uložením, u podvodních betonových základů se zpětným kotvením, u podkladního betonu na pilotách, u skořepinových prvků a monolitických prefabrikovaných nádrží.

V programu RFEM nyní zadáme pracovní diagram pro drátkobeton a ověříme chování materiálu - pro účely našeho článku nejdříve pouze na jediném konečném prvku při jednoosém namáhání v tahu. Tato jednoduchá zkouška nám umožní ověřit materiálový model používaný v programu RFEM v případě přenosu jednoosého namáhání tahem.

Při nelineárním výpočtu vnitřních sil a deformace drátkobetonu se uplatňuje v tlačené oblasti parabolický pracovní diagram podle čl. 3.1.5 normy EN 1992-1-1 [4] a v tažené oblasti multilineární průběh se zohledněním pevnosti betonu v tlaku f_ctm (obr. 06). V programu RFEM je třeba použít materiálový model, který zohlední klesající větev po vzniku trhliny. Přesně toto chování vystihuje materiálový model „Izotropní poškození 2D/3D“, který nám nabízí přídavný modul RF-MAT NL programu RFEM. Materiálový model „Izotropní poškození“ jsme popsali v našem dřívějším příspěvku. 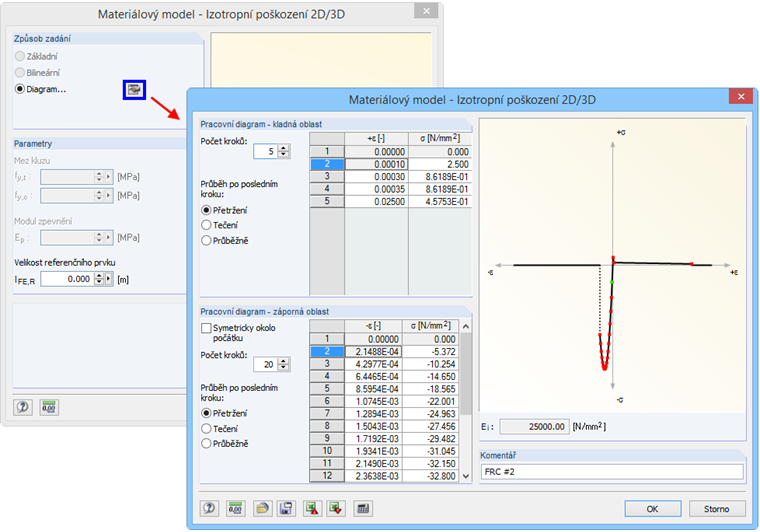Pracovní diagram se obecně zadává v programu RFEM. Pomocí volby „Diagram ...“ lze samostatně definovat tlačenou a taženou oblast. Jedině modul pružnosti na počátku musí být stejný pro příslušnou posloupnost v tlačené a tažené oblasti. Velikost referenčního prvku l_FE,R je ponechána beze změny na délce 0,0 m. Zajistíme tak, aby zadaný pracovní diagram byl při výpočtu uvažován v oblasti poškození 1:1. Na obr. 09 vidíme zadání posuzovaného drátkobetonu ve vstupním dialogu programu RFEM.

Definition der Spannungs-Dehnungs-Linie des Stahlfaserbetons

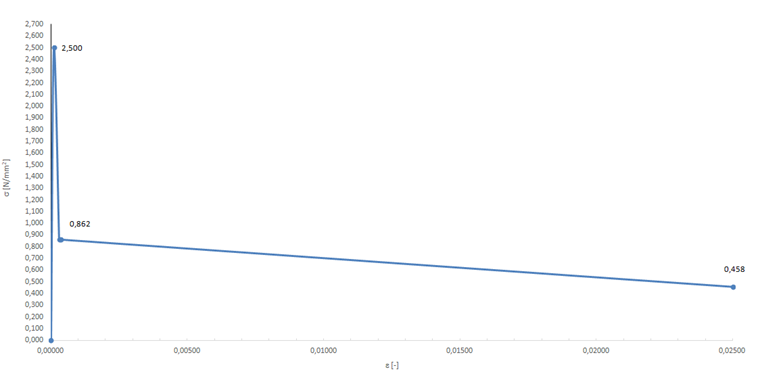
Vzhledem k tomu, že se má chování v tahu po vzniku trhliny vyšetřit důkladněji, stanoví se vlastnosti v tažené oblasti testovaného drátkobetonu podrobněji:

f_ctm = 2,500 N/mm²
1,04 ⋅ f^f_ctr,L1 = 0,862 N/mm²
1,04 ⋅ f^f_ctr,L2 = 0,458 N/mm²

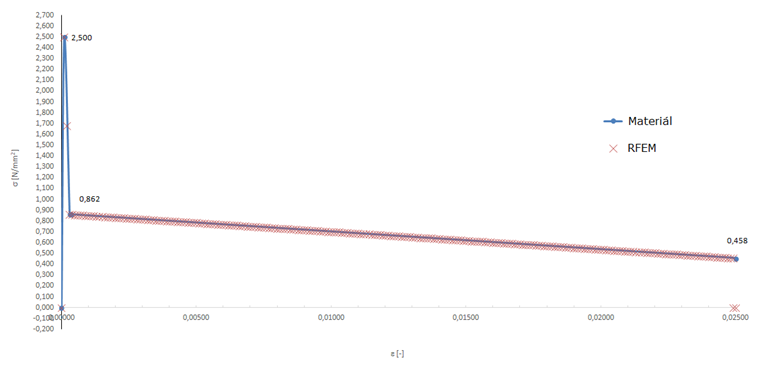
Na základě uvedených parametrů materiálu se pro taženou oblast stanoví pracovní diagram, který vidíme na obr. 10.

Výpočtový model v programu RFEM: ein FE-Element, links gehalten, rechts gezogen

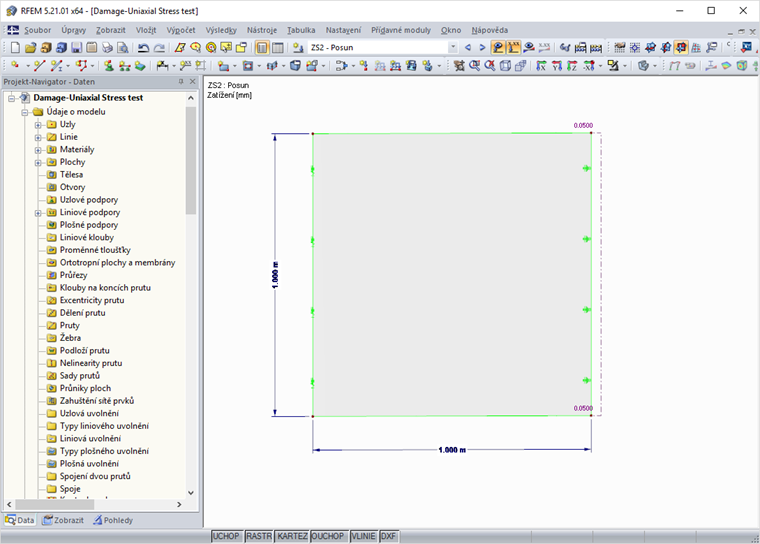
Abychom vyloučili vliv sousedících prvků a dvouosých stavů napjatosti na naše výsledky, zkontrolujeme materiál na konečném prvku s délkou stran 1 ⋅ 1 m. Prvek je přitom vodorovně podepřen na jedné straně a tažen na straně protilehlé. Pro získání obrazce pevnosti v tahu po vzniku trhliny je třeba zatížení aplikovat jako při řízené čtyřbodové ohybové zkoušce. Na obr. 11 je znázorněn výpočtový model v programu RFEM.

Vorgabe der stufenweise ansteigenden Belastung

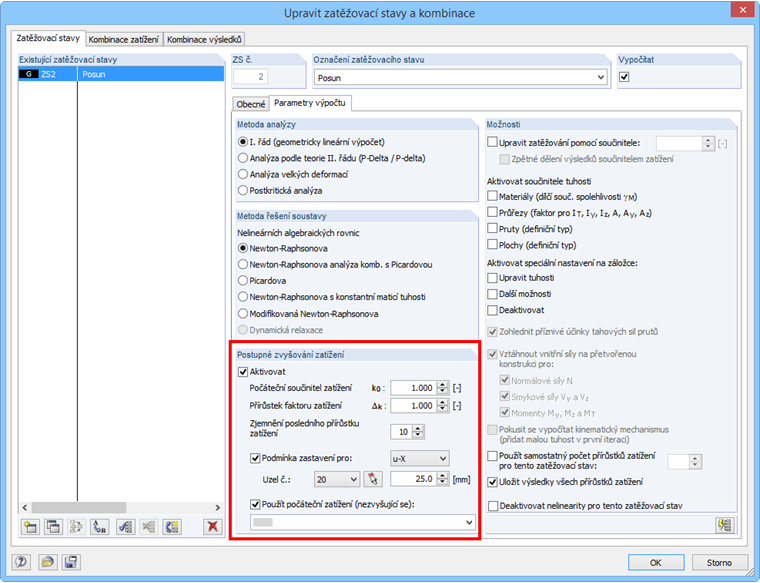
Pomocí funkce „Postupné zvyšování zatížení“ v parametrech výpočtu zatěžovacího stavu se bude deformace zvětšovat až do dosažení kritéria přerušení. Jako kritérium přerušení byl nastaven posun uzlu 25,1 mm, což odpovídá přetvoření ε 0,0251.

Darstellung der 1. Membranspannung im Berechnungsdiagramm

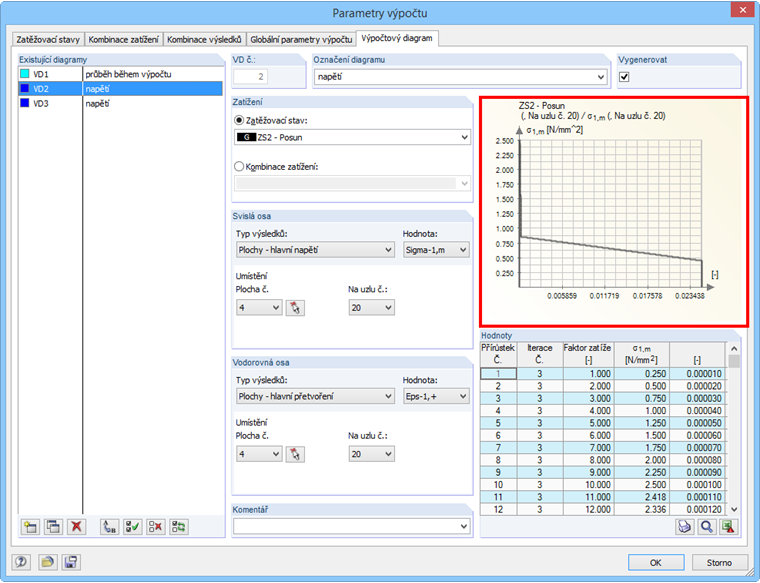
Výsledky výpočtu se vyhodnotí na membránovém napětí ve směru první hlavní osy σ_1,m. V dialogu „Parametry výpočtu“ se nám nabízí možnost nechat zobrazit průběh výsledků výpočtu při postupném zvyšování zatížení.

Gegenüberstellung der RFEM-Ergebnisse mit definierter Materialeigenschaft im Zugbereich

Vypočítané membránové napětí přesně odpovídá zadanému průběhu pevnosti v tahu po vzniku trhliny. V následujícím diagramu je hlavní napětí σ_1,m určeno pracovním diagramem pro taženou oblast drátkobetonu. Výsledky vypočítané v programu RFEM přesně odpovídají zadanému pracovnímu diagramu.

Spannungs-Dehnungs-Linie des Stahlfaserbetons im Zugbereich für eine nichtlineare Berechnung

Shrnutí

Materiálový model „Izotropní poškození 2D/3D“ umožnil přesně ověřit chování drátkobetonu po vzniku trhliny při jednoosém namáhání v tahu. Přitom je třeba dát pozor na to, aby při podobných ověřovacích výpočtech byly vyloučeny veškeré vlivy sousedících prvků, dvouosých stavů napjatosti nebo modifikací v materiálovém modelu nastavením velikosti referenčního prvku l_FE,R.

Databáze znalostí

KB 001601 | Stanovení materiálových vlastností drátkobetonu a jeho použití v programu RFEM