Ermittlung der Materialeigenschaften von Stahlfaserbeton und deren Verwendung in RFEM

Materialeigenschaften

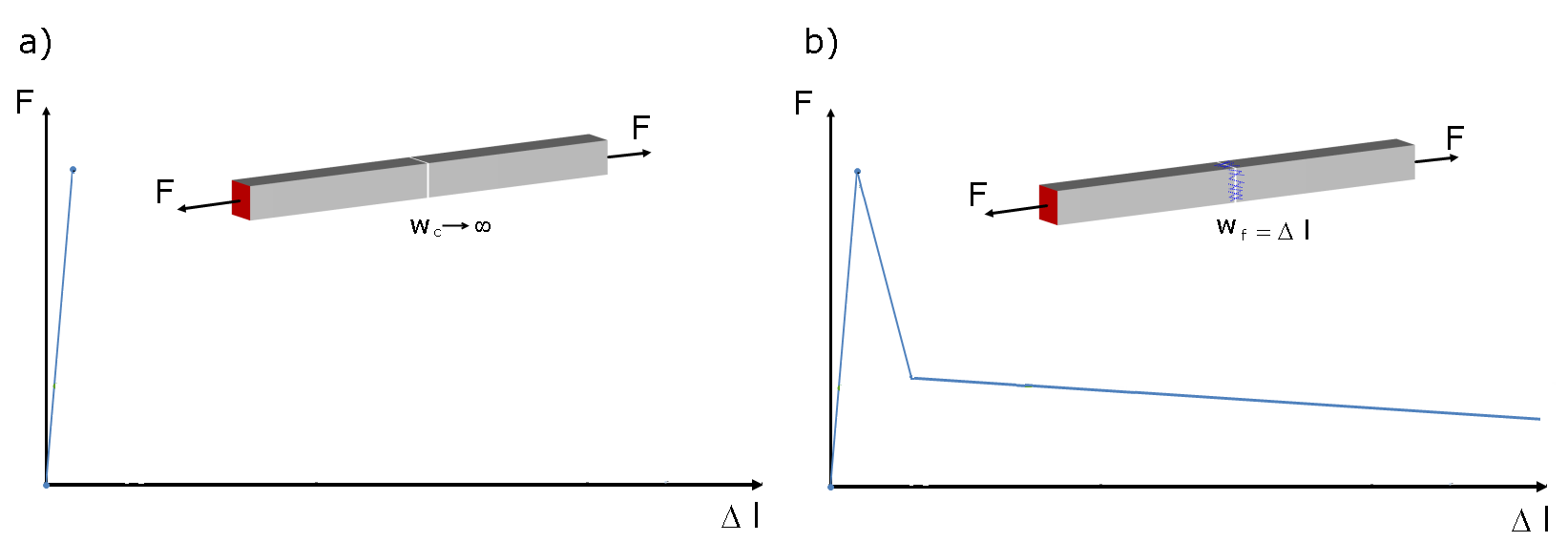
Bei Faserbeton handelt es sich um einen Beton nach DIN EN 206-1, dem zum Erreichen bestimmter Eigenschaften Stahlfaser beigegeben wird. Durch eine ausreichende Zugabe von Stahlfasern können diese im Beton Zugkräfte über den Riss hinweg übertragen. In Bild 01 ist das prinzipielle Verhalten von unbewehrtem Beton und Stahlfaserbeton auf Zug gegenübergestellt. Dort kann man erkennen, dass der Zugwiderstand des Stahlfaserbetons mit größer werdender Verformung abnimmt, die Last-Verformungs-Kurve weist nach Erreichen der Zugfestigkeit einen abfallenden Ast auf.

Last-Verformungs-Verhalten von a) unbewehrtem Beton und b) Stahlfaserbeton

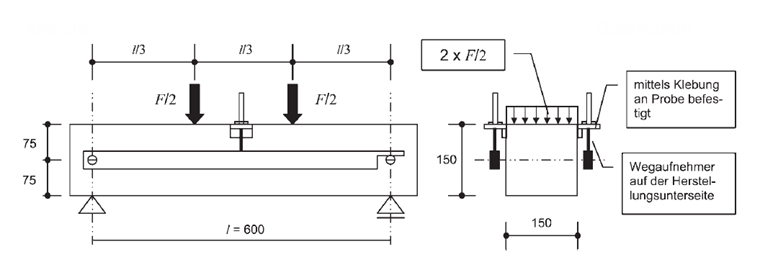
Die Festigkeit des Verbundwerkstoffes Stahlfaserbeton nach Überschreitung der Betonzugfestigkeit wird Nachrisszugfestigkeit genannt. Dabei werden die tatsächlich in den Stahlfasern auftretenden Zugkräfte auf die Fläche der Betonzugzone bezogen. Die Nachrisszugfestigkeit wird in der Regel mittels eines Biegezugversuches nach [1] im Baustofflabor bestimmt. Als Probekörper werden dabei Balken mit den Abmessungen b/h/l = 150 mm / 150 mm / 700 mm eingesetzt. Da für die Arbeitslinie des Stahlfaserbetons das Biegezugverhalten im Nachrissbereich von Bedeutung ist, wird der 4-Punkt-Biegeversuch weggesteuert durchgeführt. Bild 02 zeigt die vermaßte zeichnerische Darstellung des 4-Punkt-Biegeversuches.

Prüfeinrichtung zur Ermittlung der Nachrissbiegezugfestigkeit (Abmessungen in mm)

Aufgrund des Versuchsaufbaus des 4-Punkt-Biegeversuches kann sich die Rissstelle vollkommen frei am Versuchsbalken einstellen, da die lokale Beanspruchung zwischen den beiden Belastungspunkten konstant ist. Im nachfolgenden Bild sieht man am abgeschlossenen Versuch (Presse wurde zur Vergrößerung der Rissöffnung nach dem Abschluss des Experimentes manuell noch weiter ausgefahren), dass sich die Rissbildung frei zwischen den beiden Pressenrollen an der maßgebenden Stelle (= schwächste Stelle) einstellt.

Abgeschlossener 4-Punkt-Biegeversuch mit Rissöffnung (Bild: BPL Müller und Lobisch GmbH)

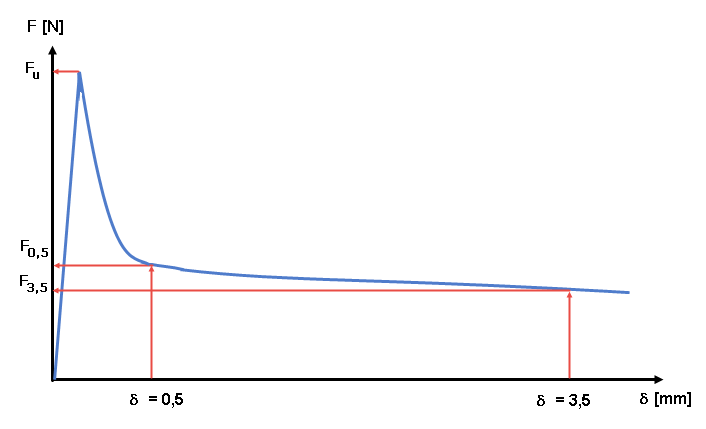
Die Prüfergebnisse werden in einer Last-Verformungskurve dokumentiert (siehe Bild 04). Aus dieser Last-Verformungs-Kurve werden die sogenannten äquivalenten Biegezugfestigkeiten und daraus mit Hilfe von Umrechnungsfaktoren die Nachrisszugfestigkeit des Stahlfaserbetons ermittelt. Man unterscheidet dabei zwischen einem Kennwert für die Beurteilung des Grenzzustandes der Gebrauchstauglichkeit (= kleine Verformungen, δ = 0,5 mm) und einem maßgebenden Kennwert für den Bruchzustand (= große Verformungen, δ = 3,5 mm).

Symbolische Last-Verformungs-Kurve zur Ermittlung der Nachrisszugfestigkeiten

Die Nachrissbiegezugfestigkeiten des Stahlfaserbetons sind aus den Belastungswerten F_0,5 bei δ = 0,5 mm und F_3,5 bei δ = 3,5 mm zu ermitteln. Dabei wird die erreichte Last L_i (mit i=0,5 beziehungsweise 3,5) mit dem zugehörigem Lasthebelarm multipliziert und durch das Widerstandsmoment W_j des ungerissenen Querschnittes dividiert. Die mittlere Nachrissbiegezugfestigeit f^f_cflm,Li einer Versuchsreihe aus n Püfbalken ergibt sich als arithmetisches Mittel der einzelnen Nachrisszugfestigkeiten.

Zur Klassifizierung des Verbundwerkstoffes Stahlfaserbeton sieht die DAfStb-Richtlinie Stahlfaserbeton zwei unterschiedliche Leistungsklassen L1 und L2 vor. Die Leistungsklasse L1 beschreibt die Materialeigenschaften für kleine Verformungen (δ = 0,5 mm) und die Leistungsklasse L2 das Verhalten für größere Verformungen (δ= 3,5 mm). Die Bezeichnung der Leistungsklassen Li entspricht dem charaktristischen Wert der Nachrissbiegezugfestigkeit f^f_cflk,Li in N/mm² für die entsprechenden Verformungen. Die charakteristische Nachrissbiegezugfestigkeit berechnet sich gemäß [1] folgendermaßen aus der mittleren Nachrissbiegezugfestigkeit f^f_cflm,Li.

Dabei ist
Lf^f_cflm,Li ... Mittelwert der logarithmierten Einzelprüfergebnisse f^f_cfl,Li,j (Details siehe [1])
L_s ... Standardabweichung der logarithmierten Einzelprüfergebnisse (Details siehe [1]
k_s ... Fraktilenkorrekturfaktor für unbekannte Standardabweichungen für das 5-%-Fraktil mit 75 % Aussagewahrscheinlichkeit (Details siehe [1])

Die Bezeichnung des Stahlfaserbetons erfolgt somit durch die Ergänzung des Buchstabens L für Leitungsklasse mit der charakteristischen Nachrissbiegezugfestigkeit für die Vorformungen 1 (GZG) und 2 (GZT). Ein Stahlfaserbeton C30/37 L0,9/ L0,6 XC1 hat beispielsweise eine charakteristische Nachrissbiegezugfestigkeit von 0,9 N/mm² für die Verformung 1 und 0,6 N/mm² für die Verformung 2.

Spannungs-Dehnungs-Linie des Stahlfaserbetons

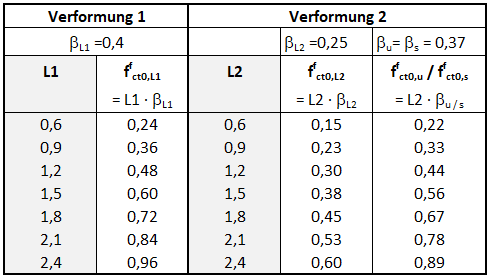
Für die Bemessung von Stahlfaserbetonbauteilen benötigt man Spannungs-Dehnungs-Linien. Hierfür werden die vorher beschriebenen charakterischtischen Nachrissbiegezugfestigkeiten f^f_cflk,Li mit Hilfe von β-Faktoren in zentrische Nachrisszugfestigkeiten f^f_ct0,i gemäß [1] umgerechnet. In der Tabelle R3 der DAfStb-Richtlinie Stahlfaserbeton [1] werden die Grundwerte der zentrischen Nachrisszugfestigkeit f^f_ct0,i für die jeweiligen Leistungsklassen bereits angegeben (siehe Bild 05).

Gebräuchlichste Leistungsklassen L1 und L2 mit zugehörigen Grundwerten der zentrischen Nachrisszugfestigkeit

Um die Rechenwerte f^f_ctR,i für die Spannungs-Dehnungs-Linie zu erhalten, sind die Grundwerte der zentrischen Nachrisszugfestigkeit noch mit zwei Korrekturfaktoren κ^f_G und κ^f_F zu modifizieren.

f^f_ctR,i = κ^f_G ⋅ κ^f_F ⋅ f^f_ct0,i

Dabei ist
κ^f_G ... Faktor zur Berücksichtigung des Einflusses der Bauteilgröße auf den Variationskoeffizienten = 1,0 + A^f_ct ⋅ 0,5 < 1,70
A_ct ... zum jeweiligen Gleichgewichtszustand gehörige, unter Zugspannung stehende Querschnittsfläche der gerissenen Bereiche in m²
κ^f_F ... Faktor zur Berücksichtigung der Faserorientierung = 0,5. Bei ebenen, liegend hergestellten flächenhaften Bauteilen (b < 5) darf κ^f_F = 1,0 bei Biege- und Zugbeanspruchung angenommen werden.

Die Stahlfaserrichtlinie [1] geht davon aus, dass die Verformung 1 mit δ = 0,5 mm des 4-Punkt-Biegeversuches einer Dehnung von ε = 0,0035 und die Verformung 2 mit δ = 3,5 mm einer Dehnung ε = 0,025 entsprechen.

Je nach vorgesehener Berechnung stehen in [1] für den Zugbereich verschiedene Spannungs-Dehnungs-Linien zur Verfügung. Für eine nichtlineare Verformungs- und Schnittgrößenermittlung ist im Zugbereich die in Bild 06 dargestellte multilineare Beziehung anzusetzen. Dabei ist der lineare Verlauf bis zum Erreichen der Betonzugfestigkeint f_ctm ansetzbar. Die in Bild 06 blau dargestellte Spannungs-Dehnungs-Linie ist gemäß [1] nur für Stahlfaserbeton mit einen Verhältnis von L2 / L1 ≥ 0,7 zulässig. Bei Leistungsklassenverhältnissen L2 / L1 ≤ 0,7 ist nur noch der Ansatz des Spannungsblockes (grün gestrichelte Linie in Bild 06) erlaubt.

Spannungs-Dehnungs-Linie im Zugbereich nach [1] für die Schnittgrößen- und Verformungsermittlung bei nichtlinearen Verfahren

Für die Querschnittbemessung im Grenzzustand der Tragfähigkeit darf die Betonzugfestigkeit f_ctm nicht angesetzt werden. Die ansetzbare zusätzliche Zugfestigkeit kommt lediglich aus der durch die Stahlfasern übertragene Zugkraft im Riss. Des Weiteren sind die Zugfestigkeiten für den Nachweis der Tragfähigkeit mit den Bemessungswerten f^f_ctd,Li anzusetzen. Diese ergeben sich mit der Multiplikation der Rechenwerte f^f_ctR,Li mit den Abminderungsfaktor α^f_c und der Division mit dem Teilsicherheitsbeiwert γ^f_ct. Der Ansatz von f^f_ctd,L1 und f^f_ctd,L2 (blau durchgezogene Linie in Bild 7) ist auf Verhältnisse von L2 / L1 ≥ 0,7 beschränkt. Der in Bild 07 grün gestrichelt dargestellte Spannungsblock darf vereinfacht für Verhältnisse L2 / L1 ≤ 1 verwendet werden.

Spannungs-Dehnungs-Linie auf der Zugseite gemäß [1] für die Querschnittsbemessung im Grenzzustand der Tragfähigkeit

Im Druckbereich der Spannungs-Dehnungs-Linie für den Stahlfaserbeton gibt es keinen Unterschied zwischen Normalbeton ohne Fasern und Stahlfaserbeton. Für die Spannungs-Dehnungs-Beziehung im Druckbereich gilt unverändert die Regelung von EN 1992-1-1 [4]. Demnach ist für die nichtlineare Berechnung der Verfomung und Schnittgrößen ein parabelförmiger Verlauf gemäß Kapitel 3.1.5 [4] (siehe Bild 08 a) beziehungsweise für die Bemessung ein Parabel-Rechteck nach Kapital 3.1.6 [4] für die Spannungs-Dehnungs-Linie im Druckbereich zu verwenden.

Spannungs-Dehnungs-Linie nach [4] für den Druckbereich: a) für die nichtlineare Berechnung; b) für die Querschnittsbemessung

Nichtlineare Berechnung mit RFEM

Nichtlineare Verfahren dürfen gemäß [1] bei Stahlfaserbetonbauteilen grundsätzlich angewendet werden, wenn die überwiegende Tragwirkung durch Betonstahl erzielt wird. In allen anderen Fällen ist die nichtlineare Berechnung nur für elastisch gebettete Bauteile, rückverankerte Unterwasserbetonsohlen, pfahlgestützte Bodenplatten, schalenförmige Bauteile und monolitisch hergestellte Fertigteilbehälter anwendbar.

Nachfolgend wird in RFEM die Spannungs-Dehnungs-Linie für einen Stahlfaserbeton definiert und das Materialverhalten kontrolliert. Im Zuge dieses Artikels wird dies zunächst nur an einem FE-Element mit einer einachsigen Zugbelastung durchgeführt. Mittels dieses einfachen Tests soll das in RFEM verwendete Materialmodell zur Aufnahme einer einachsigen Zugbelastung verifiziert werden.

Für eine nichtlineare Schnittgrößen- und Verformungsberechnung von Stahlfaserbeton besteht die anzusetzende Spannungs-Dehnungs-Linie im Druckbereich aus einer Parabel gemäß 3.1.5 EN 1992-1-1 [4] und im Zugbereich aus dem multiliniearen Verlauf mit Berücksichtigung der Betonzugfestigkeit f_ctm (Bild 06). Es muss in RFEM ein Materialmodell verwendet werden, welches den abfallenden Ast nach der Rissbildung abbilden kann. Mit dem Zusatzmodul RF-MAT NL kann in RFEM mit dem Materialmodell "Isotrope Beschädigung 2D/3D" genau dieses Verhalten abgebildet werden. In einem früheren Artikel wurde das Materialmodell "Isotrope Beschädigung" bereits detailliert beschrieben. 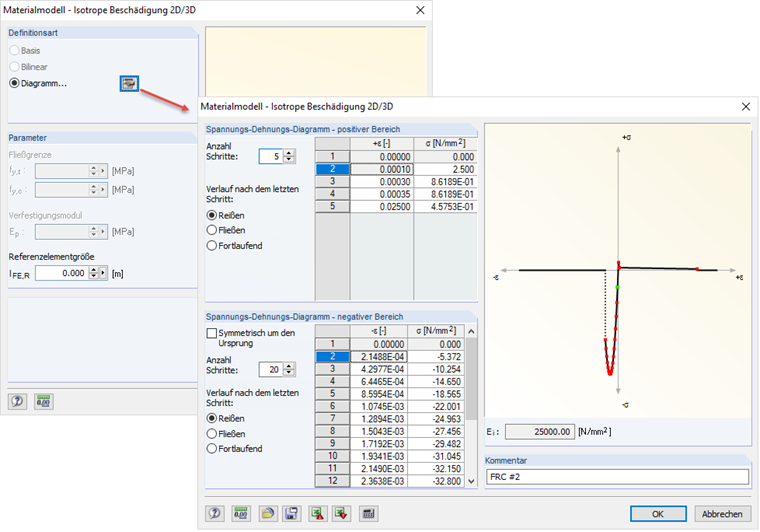Die Eingabe der Spannungs-Dehnungs-Linie ist in RFEM allgemein gehalten. Druck- und Zugbereich können individuell durch die Eingabeoption "Diagramm..." definiert werden. Einzig der Elastizitätsmodul im Ursprung muss zu den jeweiligen Nachfolgepunkten im Druck- und Zugbereich identisch sein. Die Referenzelementgröße l_FE,R wird unverändert mit einer Länge von 0,0 m belassen. Damit ist sichergestellt, dass die definierte Spannungs-Dehnungs-Linie im Schädigungsbereich 1:1 in der Berechnung angesetzt wird. Bild 09 zeigt die Eingabe des untersuchten Stahlfaserbetons in die Eingabemaske von RFEM.

Definition der Spannungs-Dehnungs-Linie des Stahlfaserbetons

Da nachfolgend die Abbildung des Nachrisszugverhaltens näher untersucht werden soll, werden die Eigenschaften im Zugbereich des getesteten Stahlfaserbetons nachfolgend detailliert beschrieben:

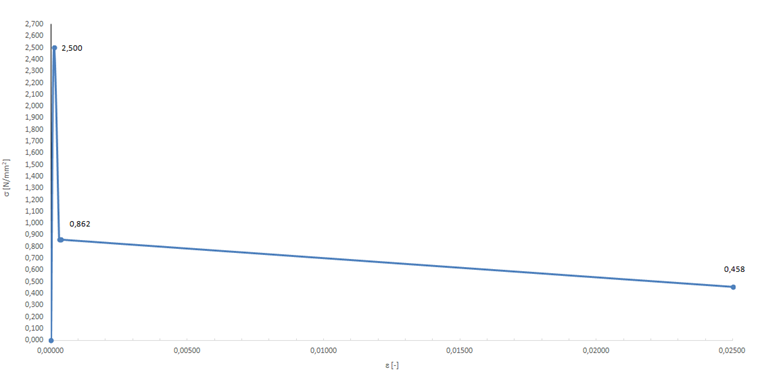
f_ctm = 2,500 N/mm²
1,04 ⋅ f^f_ctr,L1 = 0,862 N/mm²
1,04 ⋅ f^f_ctr,L2 = 0,458 N/mm²

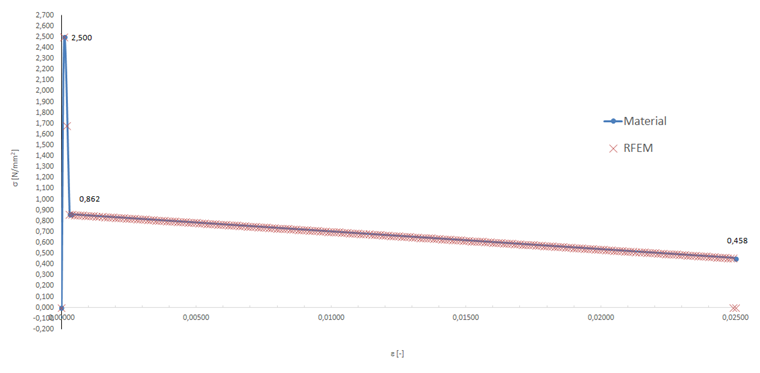
Aus den vorgenannten Materialparamatern ergibt sich im Zugbereich die in Bild 10 gezeigte Spannungs-Dehnungs-Linie.

Berechnungsmodell in RFEM: ein FE-Element, links gehalten, rechts gezogen

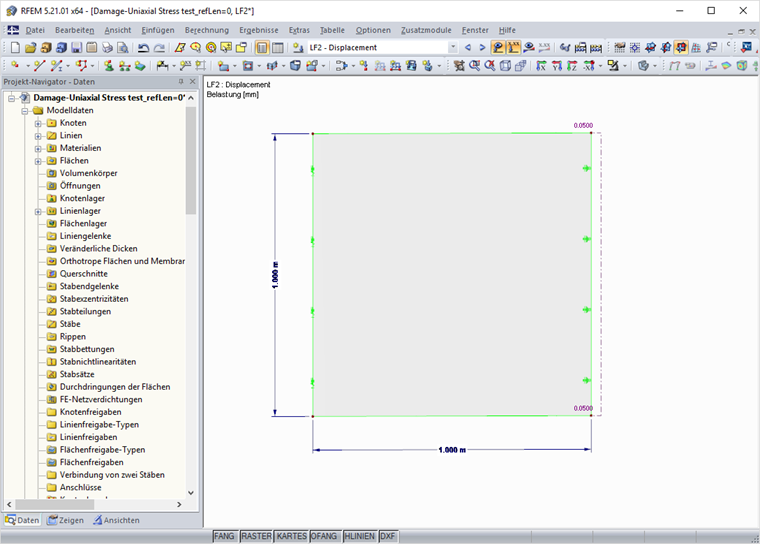
Um den Einfluss von Nachbarelementen und zweichsigen Spannungzuständen auf die Ergebnisse zu vermeiden, wird das Material an einem finiten Element mit den Seitenlängen 1 ⋅ 1 m überprüft. Das Element wird dabei an einer Elementseite horizontal gehalten und an der gegenüberliegend gezogen. Um das Bild der Nachrisszugfestigkeit zu erhalten, muss die Belastung wie beim oben beschriebenen 4-Punkt-Biegeversuch weggesteuert aufgebracht werden. Bild 11 zeigt das Berechnungsmodell in RFEM.

Vorgabe der stufenweise ansteigenden Belastung

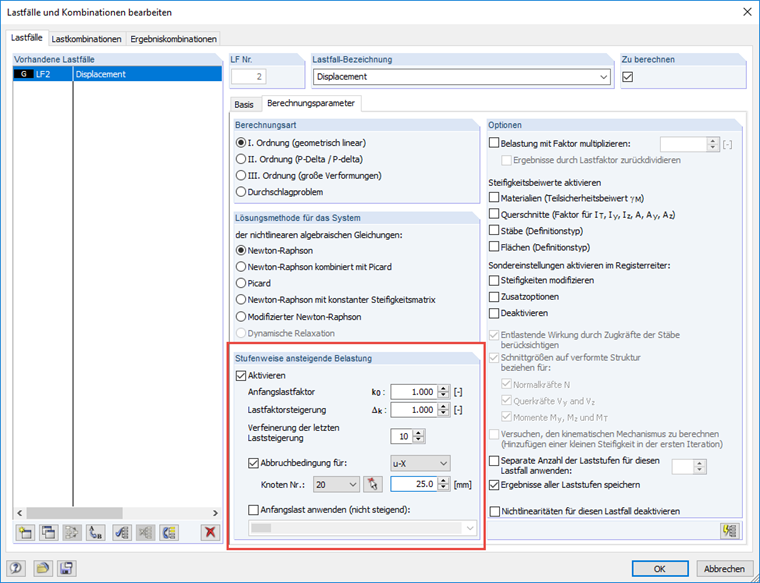
Durch die Verwendung der Funktion "Stufenweise ansteigende Belastung" in den Berechnungsparametern des Lastfalles wird die Verformung bis zum Erreichen des Abbruchkriteriums gesteigert. Das verwendete Abbruchkriterium wurde mit einer Knotenverschiebung von 25,1 mm definiert, was einer Dehnung ε von 0,0251 entspricht.

Darstellung der 1. Membranspannung im Berechnungsdiagramm

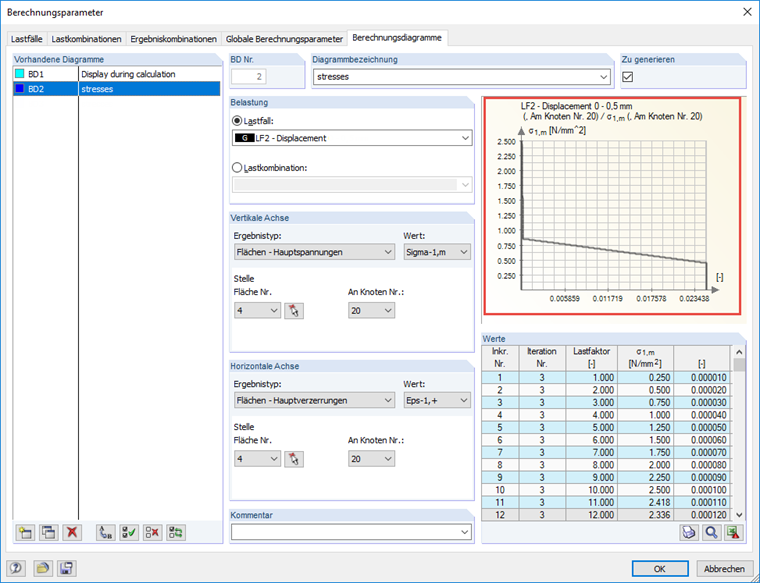
Zur Auswertung der Berechnungsergebnisse wird die Membranspannung in Richtung der 1. Hauptachse σ_1,m verwendet. Im Dialog "Berechnungsparamter" besteht die Möglichkeit, ein Diagramm für die Berechnungsergebnisse bei einer stufenweise Laststeigerung anzeigen zu lassen.

Gegenüberstellung der RFEM-Ergebnisse mit definierter Materialeigenschaft im Zugbereich

Die berechenete Membranspannung folgt genau dem vorgegebenen Verlauf der Nachrisszugfestigkeit. Im nachfolgenden Diagramm wird die Hauptspannung σ_1,m über die im Zugbereich definierte Spannungs-Dehnungs-Linie des Stahlfaserbetons gelegt. Die in RFEM berechneten Ergebnisse passen genau mit der definierten Arbeitslinie zusammen.

Spannungs-Dehnungs-Linie des Stahlfaserbetons im Zugbereich für eine nichtlineare Berechnung

Zusammenfassung

Durch die Verwendung des Materialmodells "Isotrope Beschädigung 2D/3D" konnte exakt das Nachrissverhalten des Stahlfaserbetons bei einachsiger Zugbelastung verifiziert werden. Dabei ist zu beachten, dass bei solchen Verifizierungsberechnungen sämtliche Einflüsse aus beispielsweise Nachbarelementen, mehrachsigen Spannungszuständen oder Modifikationsmöglichkeiten im Materialmodell mittels der Vorgabe einer Referenzelementgröße l_FE,R ausgeschlossen werden.

Knowledge Base

KB 001601 | Ermittlung der Materialeigenschaften von Stahlfaserbeton und deren Verwendung in RFEM