- F.3.1 Метод средневзвешенного значения
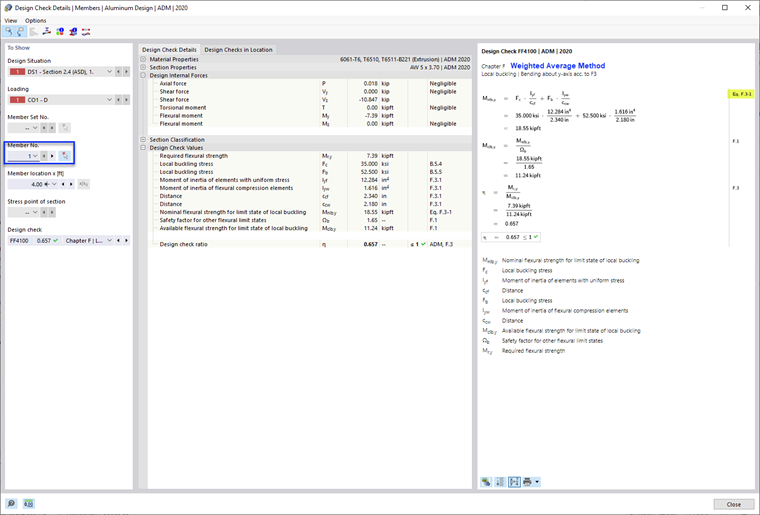
Это наиболее распространенный метод, используемый в примерах ADM и метод по умолчанию в RFEM 6. The weighted average method combines strengths determined separately for each element using equation F.3-1 of ADM 2020 [1].
- F.3.2 Прямой метод прочности
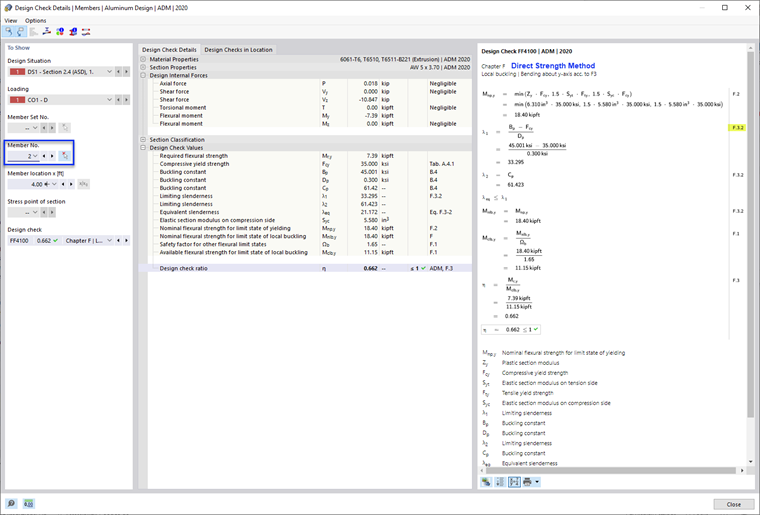
В данном методе прочность при местном выпучивании поперечного сечения как одного целого определяется путем анализа, который непосредственно включает взаимодействие элементов. Этот метод является наиболее точным и полным из всех трех.
- F.3.3 Метод граничного элемента
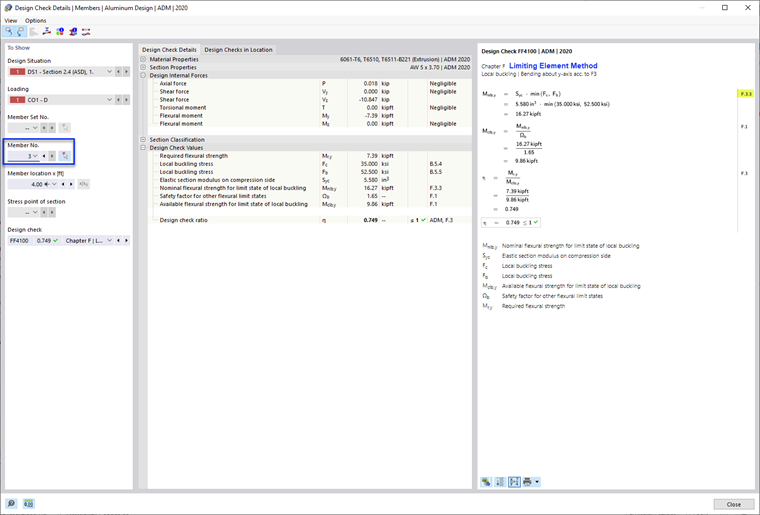
Этот метод ограничивает прочность стержня на изгиб на основе самой низкой прочности на изгиб среди всех элементов. This method is often less accurate and more conservative, since it does not account for the interaction between elements.
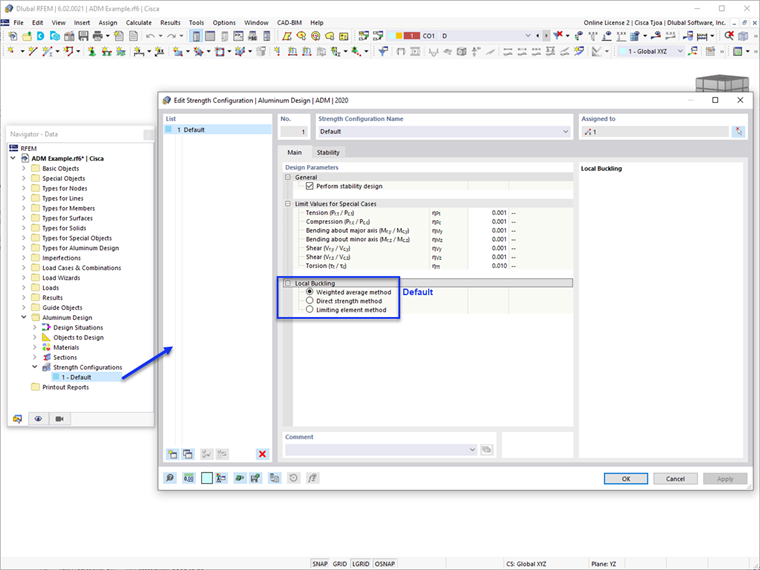
All three methods used in Section F.3 to determine the local buckling strengths reference Sections B.5.4 and B.5.5. Эти разделы включают определение прочности элементов при равномерном сжатии и элементов при изгибном сжатии. Прочность при местном выпучивании кроме прочего зависит от того, поддерживается ли элемент на одном или на обеих концах, а также от соотношения ширины к толщине, b/t.
Comparison of RFEM Results Using Three Different Methods
The local buckling strength of an aluminum beam in Example 3 of the ADM is compared to the RFEM results using the three different methods described above.
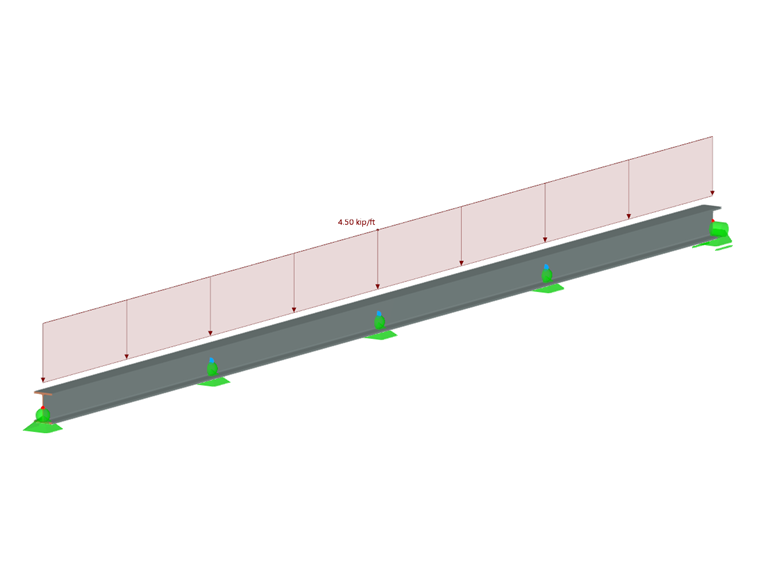
AW 5 x 3.70 section and 6061-T6 (B221) material is used for the 16-foot-long beam. Балка имеет непрерывную боковую опору, а расстояние между вертикальными опорами по центру - 4,0 фута. It supports a uniform dead load of 4.50 k/ft (Image 2).
Характеристики сечения показаны на рисунке 3.
Напряжения местного выпучивания полки и стенки необходимы для определения номинальной прочности стержня на изгиб.
Напряжение при местном выпучивании полки
Полка (плоский элемент, опирающийся на одну кромку) подвержена равномерному сжатию. Its local buckling stress is determined according to Section B.5.4.1.
The slenderness ratio b/t is equal to [(3.5 in -0.19 in - 2*0.30 in)/2] / 0.32 in = 4.234
The slenderness factor λ1 = 6.7 can be found using the equation listed in Section B.5.4.1 or taken directly from Table 2-19 of Part VI.
Since b/t = 4.234 is less than λ1 = 6.7, the yielding limit state controls. Therefore, the uniform compressive stress
Fc = Fcy = 35.0 ksi (Table A.4.1 & Table A.4.3).
Напряжение при местном выпучивании стенки
Стенка (плоский элемент, опирающийся на две кромки) подвержена изгибающему сжатию. Its local buckling stress is determined according to Section B.5.5.1.
The slenderness ratio b/t is equal to [(5.0 in -2*0.32 in -2*0.3 in)] / 0.19 in = 19.789
The slenderness factor λ1 = 33.1 can be found using the equation listed in Section B.5.5.1 or taken directly from Table 2-19 of Part VI.
Since b/t = 19.789 is less than λ1 = 33.1, the yielding limit state controls. Therefore, the flexural compressive stress, Fb = 1.5*Fcy = 1.5*35.0 ksi = 52.5 ksi (Table A.4.1 & Table A.4.3).
В подробностях расчета в RFEM 6 приведены формулы и ссылки, используемые в каждом методе. Результаты каждого метода можно легко проверить.
- Nominal Flexural Strength, Mnlb as per F.3.1 Weighted Average Method
- Nominal Flexural Strength, Mnlb as per F.3.2 Direct Strength Method
- Nominal Flexural Strength, Mnlb as per F.3.3 Limiting Element Method
This is the method used in Example 3 [1]. Незначительная разница в коэффициенте использования обусловлена уравнением балки, используемым для определения максимального требуемого изгибающего момента.
Заключение
In this example, the design check ratios of the Weighted Average Method and Direct Strength Method are almost identical (0.657 and 0.662). Как и ожидалось, метод граничного элемента является наиболее консервативным и имеет самый высокий расчетный коэффициент использования (0,749).
.png?mw=760&hash=532a9ec54f1f2d64bc51a71a0a76e52cce2b8524)