- F.3.1 Método del promedio ponderado
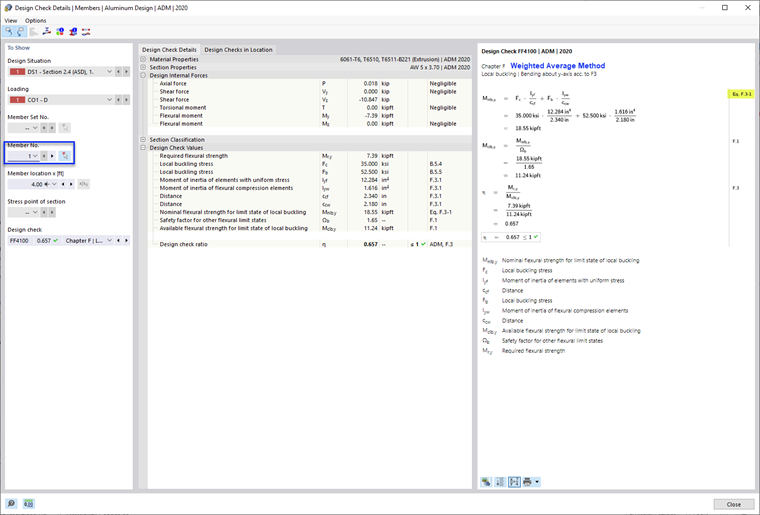
Este es el método más común utilizado en los ejemplos de ADM y la opción predeterminada en RFEM 6. The weighted average method combines strengths determined separately for each element using equation F.3-1 of ADM 2020 [1].
- F.3.2 Método de la resistencia límite
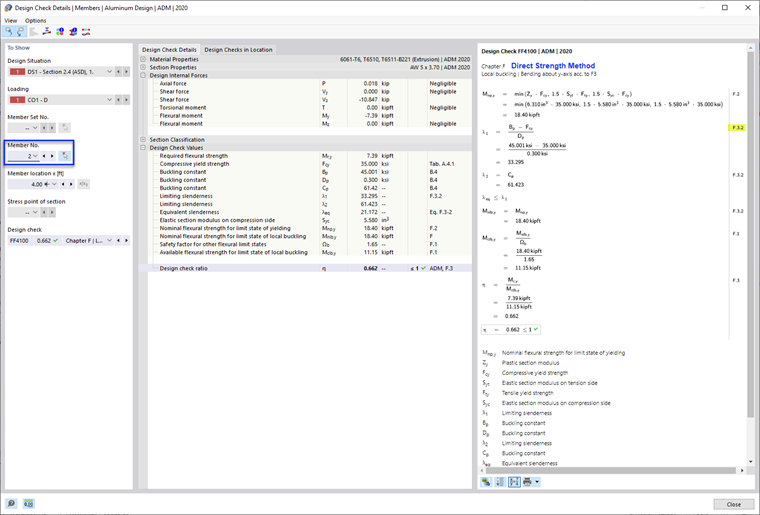
En este método, la resistencia al pandeo local de la sección en su conjunto se determina mediante un análisis que incluye directamente la interacción de los elementos. Este método es el más preciso y completo de los tres.
- F.3.3 Método del elemento limitador
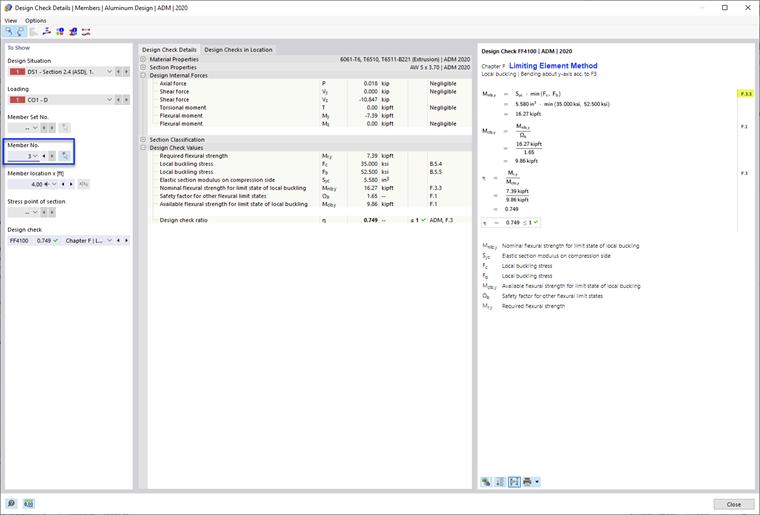
Este método limita la resistencia a la flexión de la barra en función de la resistencia al pandeo local más baja de todos los elementos. This method is often less accurate and more conservative, since it does not account for the interaction between elements.
All three methods used in Section F.3 to determine the local buckling strengths reference Sections B.5.4 and B.5.5. Estas secciones incluyen la determinación de la resistencia de los elementos en compresión uniforme y elementos en compresión a flexión. La resistencia al pandeo local depende además de si el elemento está apoyado en uno o ambos bordes, además de la relación entre el ancho y el espesor b/t.
Comparison of RFEM Results Using Three Different Methods
The local buckling strength of an aluminum beam in Example 3 of the ADM is compared to the RFEM results using the three different methods described above.
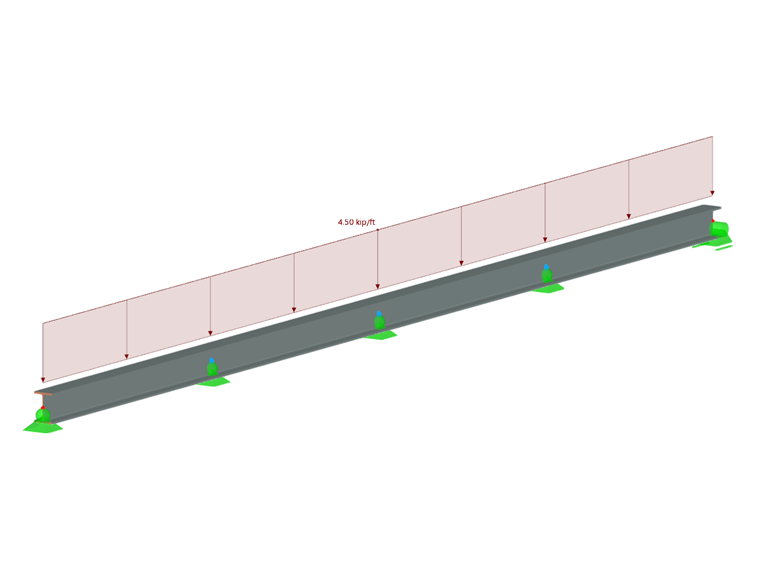
AW 5 x 3.70 section and 6061-T6 (B221) material is used for the 16-foot-long beam. La viga tiene un apoyo lateral continuo y una separación de apoyo vertical a 4,0 pies (1,2 m) en el centro. It supports a uniform dead load of 4.50 k/ft (Image 2).
Las propiedades de la sección se muestran en la Imagen 3.
.png?mw=760&hash=532a9ec54f1f2d64bc51a71a0a76e52cce2b8524)
Las tensiones de pandeo locales del ala y del alma son necesarias para determinar la resistencia nominal a la flexión de la barra.
Tensión de pandeo local del ala
El ala (un elemento plano apoyado en un borde) está en compresión uniforme. Its local buckling stress is determined according to Section B.5.4.1.
The slenderness ratio b/t is equal to [(3.5 in -0.19 in - 2*0.30 in)/2] / 0.32 in = 4.234
The slenderness factor λ1 = 6.7 can be found using the equation listed in Section B.5.4.1 or taken directly from Table 2-19 of Part VI.
Since b/t = 4.234 is less than λ1 = 6.7, the yielding limit state controls. Therefore, the uniform compressive stress
Fc = Fcy = 35.0 ksi (Table A.4.1 & Table A.4.3).
Tensión de pandeo local del alma
El alma (un elemento plano apoyado en dos bordes) está en compresión por flexión. Its local buckling stress is determined according to Section B.5.5.1.
The slenderness ratio b/t is equal to [(5.0 in -2*0.32 in -2*0.3 in)] / 0.19 in = 19.789
The slenderness factor λ1 = 33.1 can be found using the equation listed in Section B.5.5.1 or taken directly from Table 2-19 of Part VI.
Since b/t = 19.789 is less than λ1 = 33.1, the yielding limit state controls. Therefore, the flexural compressive stress, Fb = 1.5*Fcy = 1.5*35.0 ksi = 52.5 ksi (Table A.4.1 & Table A.4.3).
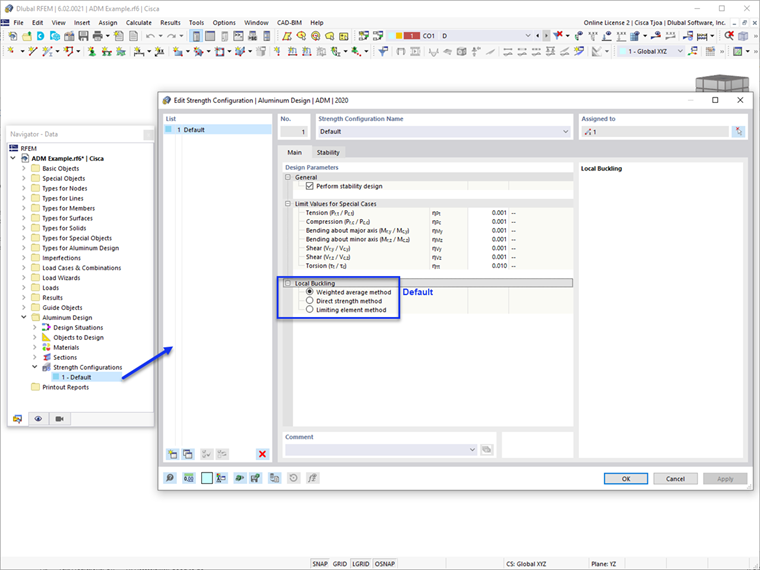
Los detalles de verificación de diseño en RFEM 6 proporcionan las ecuaciones y referencias utilizadas en cada método. El resultado de cada método se puede verificar fácilmente.
- Nominal Flexural Strength, Mnlb as per F.3.1 Weighted Average Method
- Nominal Flexural Strength, Mnlb as per F.3.2 Direct Strength Method
- Nominal Flexural Strength, Mnlb as per F.3.3 Limiting Element Method
This is the method used in Example 3 [1]. La diferencia despreciable en la relación de utilización proviene de la fórmula de la viga utilizada para determinar el momento flector máximo requerido.
Conclusión
In this example, the design check ratios of the Weighted Average Method and Direct Strength Method are almost identical (0.657 and 0.662). Y, como se esperaba, el método del elemento limitador es el más conservador y tiene la relación de comprobación de diseño más alta (0,749).
Base de datos de conocimientos