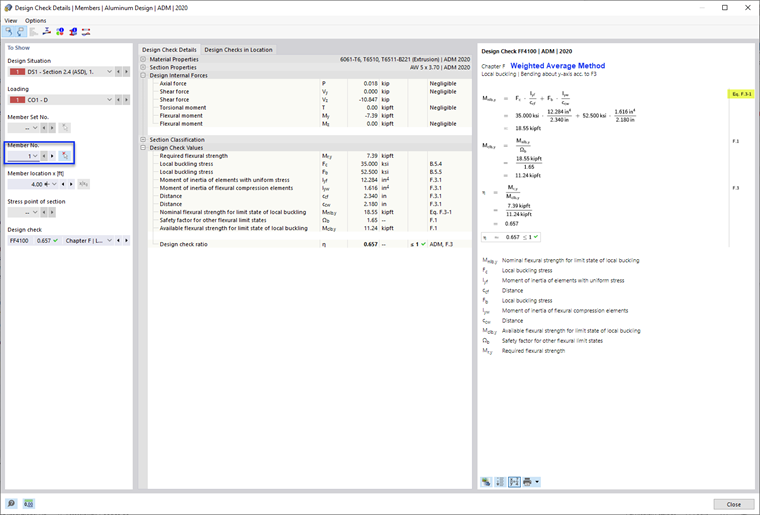
- F.3.1 Methode des gewichteten Durchschnitts
Dies ist die in den ADM-Beispielen am häufigsten verwendete Methode und die Standardoption in RFEM 6. The weighted average method combines strengths determined separately for each element using equation F.3-1 of ADM 2020 [1].
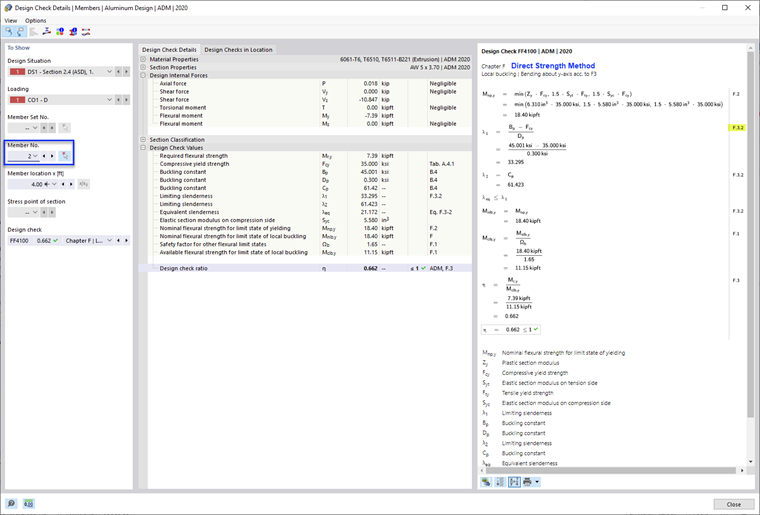
- F.3.2 Direkte Festigkeitsmethode
Bei diesem Verfahren wird die lokale Beulfestigkeit des Gesamtquerschnitts durch eine Theorie ermittelt, die das Zusammenspiel der Elemente direkt einbezieht. Diese Methode ist die genaueste und umfassendste der drei Methoden.
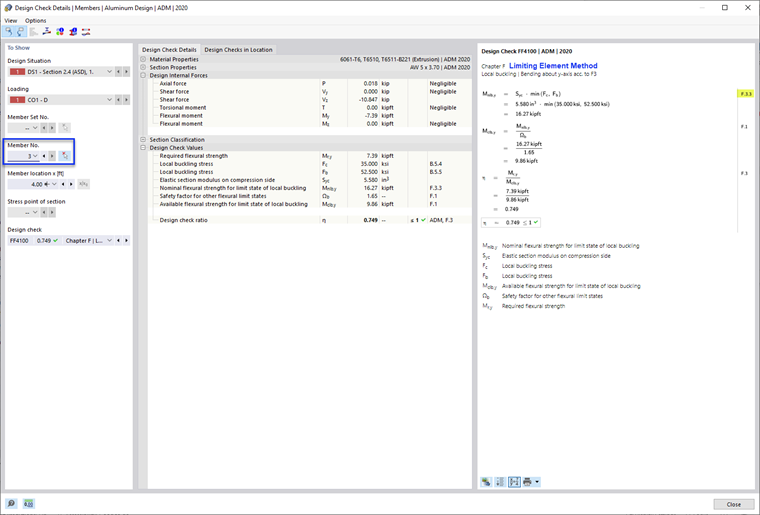
- F.3.3 Methode der Begrenzungselemente
Diese Methode begrenzt die Biegefestigkeit des Stabes anhand der niedrigsten lokalen Beulfestigkeit aller Elemente. This method is often less accurate and more conservative, since it does not account for the interaction between elements.
All three methods used in Section F.3 to determine the local buckling strengths reference Sections B.5.4 and B.5.5. Diese Abschnitte beinhalten die Bestimmung der Festigkeit von Elementen unter reinem Druck und von Elementen unter Biegedruck. Zusätzlich zum Breiten-Dicken-Verhältnis, b/t, hängt die lokale Beulstabilität außerdem davon ab, ob das Element an einem Rand oder an beiden Rändern gelagert ist.
Comparison of RFEM Results Using Three Different Methods
The local buckling strength of an aluminum beam in Example 3 of the ADM is compared to the RFEM results using the three different methods described above.
AW 5 x 3.70 section and 6061-T6 (B221) material is used for the 16-foot-long beam. Der Träger hat eine durchgehende seitliche Abstützung und einen vertikalen Auflagerabstand von 1,2 m in der Mitte. It supports a uniform dead load of 4.50 k/ft (Image 2).
Die Profileigenschaften sind in Bild 3 dargestellt.
.png?mw=760&hash=532a9ec54f1f2d64bc51a71a0a76e52cce2b8524)
Die lokalen Beulspannungen der Flansche und Stege werden zur Ermittlung der Nennbiegefestigkeit des Stabes benötigt.
Lokale Knickspannung des Flansches
Der Flansch (ein einseitig gelagertes flächiges Element) steht unter gleichmäßigem Druck. Its local buckling stress is determined according to Section B.5.4.1.
The slenderness ratio b/t is equal to [(3.5 in -0.19 in - 2*0.30 in)/2] / 0.32 in = 4.234
The slenderness factor λ1 = 6.7 can be found using the equation listed in Section B.5.4.1 or taken directly from Table 2-19 of Part VI.
Since b/t = 4.234 is less than λ1 = 6.7, the yielding limit state controls. Therefore, the uniform compressive stress
Fc = Fcy = 35.0 ksi (Table A.4.1 & Table A.4.3).
Lokale Knickspannung des Steges
Der Steg (ein zweiseitig gelagertes flächiges Element) steht unter Biegedruck. Its local buckling stress is determined according to Section B.5.5.1.
The slenderness ratio b/t is equal to [(5.0 in -2*0.32 in -2*0.3 in)] / 0.19 in = 19.789
The slenderness factor λ1 = 33.1 can be found using the equation listed in Section B.5.5.1 or taken directly from Table 2-19 of Part VI.
Since b/t = 19.789 is less than λ1 = 33.1, the yielding limit state controls. Therefore, the flexural compressive stress, Fb = 1.5*Fcy = 1.5*35.0 ksi = 52.5 ksi (Table A.4.1 & Table A.4.3).
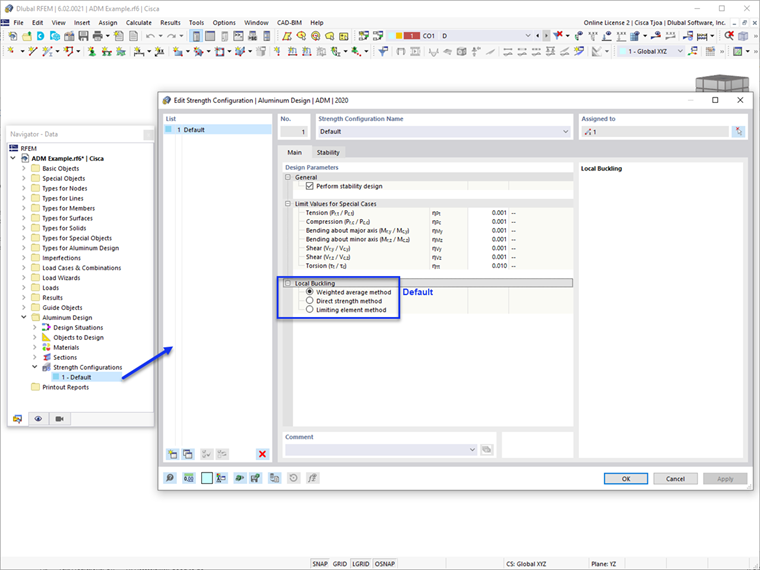
In RFEM 6 werden in den Nachweisdetails die Gleichungen und Referenzen bereitgestellt, die in jeder Methode verwendet werden. Die Ergebnisausgabe jeder Methode kann leicht überprüft werden.
- Nominal Flexural Strength, Mnlb as per F.3.1 Weighted Average Method
- Nominal Flexural Strength, Mnlb as per F.3.2 Direct Strength Method
- Nominal Flexural Strength, Mnlb as per F.3.3 Limiting Element Method
This is the method used in Example 3 [1]. Die vernachlässigbare Differenz im Ausnutzungsgrad ergibt sich aus der Trägerformel, mit der das maximal erforderliche Biegemoment ermittelt wird.
Fazit
In this example, the design check ratios of the Weighted Average Method and Direct Strength Method are almost identical (0.657 and 0.662). Und wie erwartet ist das Grenzelementverfahren das konservativste und weist das höchste Nachweisverhältnis (0,749) auf.
Knowledge Base