- F.3.1 Metoda váženého průměru
Jedná se o nejběžnější metodu používanou v příkladech ADM a také o přednastavenou volbu v programu RFEM 6. Metoda váženého průměru kombinuje pevnosti stanovené zvlášť pro každý prvek pomocí rovnice F.3-1 z ADM 2020 [1].
- F.3.2 Přímá pevnostní metoda
V této metodě se pevnost při lokálním boulení průřezu jako celku stanoví pomocí analýzy, která přímo zahrnuje interakci prvků. Tato metoda je ze všech tří metod nejpřesnější a nejkomplexnější.
- F.3.3 Metoda hraničních prvků
Tato metoda omezuje pevnost prutu v ohybu na základě nejnižší pevnosti při lokálním boulení všech prvků. Tato metoda je často méně přesná a konzervativnější, protože nezohledňuje interakci mezi prvky.
Všemi třemi metodami uvedenými v článku F.3 Lokální boulení se dosud určovala pevnost při lokálním boulení se zřetelem k článkům B.5.4 a B.5.5. Tyto články stanovují pevnost prvků v prostém tlaku a prvků v tlaku a ohybu. Kromě poměru šířky a tloušťky b/t má na stabilitu při lokálním boulení vliv to, zda je prvek podepřen na jednom konci nebo na obou koncích.
Comparison of RFEM Results Using Three Different Methods
Pevnost při lokálním boulení hliníkového nosníku v příkladu 3 v ADM je porovnána s výsledky různých výše popsaných metod v programu RFEM.
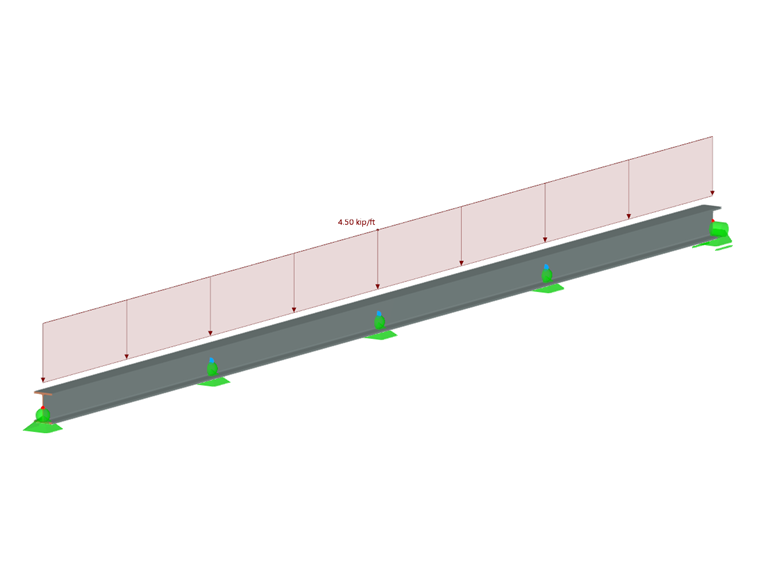
Pro 16 stop dlouhý nosník byl použit průřez AW 5 x 3,70 a materiál 6061-T6 (B221). Nosník má spojitou příčnou podporu a svislé podpory v rozestupech 4,0 stopy. Je zatížen rovnoměrným vlastním zatížením 4,50 k/ft (obrázek 2).
Průřezové charakteristiky jsou znázorněny na obrázku 3.
.png?mw=760&hash=532a9ec54f1f2d64bc51a71a0a76e52cce2b8524)
Pro stanovení jmenovité ohybové pevnosti prutu je zapotřebí napětí při lokálním boulení na pásnici a stojině.
Napětí při lokálním boulení na pásnici
Pásnice (plochý prvek podepřený na jednom okraji) je rovnoměrně zatížena tlakem. Její lokální boulení se stanoví podle kapitoly B.5.4.1.
Poměrná štíhlost b/t se rovná [(3,5 in -0,19 in - 2*0,30 in)/2] / 0,32 in = 4,234
Součinitel štíhlosti λ1 = 6,7 lze najít na základě rovnice uvedené v článku B.5.4.1 nebo přímo v tabulce 2-19 v části VI.
Protože b/t = 4,234 je menší než λ1 = 6,7, převládá mezní stav tečení. Therefore, the uniform compressive stress
Fc = Fcy = 35.0 ksi (Table A.4.1 & Table A.4.3).
Napětí při lokálním boulení na stojině
Stojina (plochý prvek podepřený na dvou okrajích) je namáhána ohybovým tlakem. Její lokální boulení se stanoví podle kapitoly B.5.5.1.
Poměrná štíhlost b/t se rovná [(5,0 in -2*0,32 in -2*0,3 in)] / 0,19 in = 19,789
Součinitel štíhlosti λ1 = 33,1 lze najít na základě rovnice uvedené v článku B.5.5.1 nebo přímo v tabulce 2-19 v části VI.
Protože b/t = 19,789 je menší než λ1 = 33,1, převládá mezní stav tečení. Proto je konstantní napětí v ohybu Fb = 1,5*Fcy = 1,5*35,0 ksi = 52,5 ksi (tabulka A.4.1 & tabulka A.4.3).
V detailech posudku v programu RFEM 6 jsou pro každou metodu uvedeny použité rovnice a odkazy. Výsledky každé metody lze snadno ověřit.
- Jmenovitá pevnost v ohybu Mnlb Metodou váženého průměru podle F.3.1
- Jmenovitá pevnost v ohybu Mnlb Přímou pevnostní metodou podle F.3.2
- Jmenovitá pevnost v ohybu Mnlb Metodou hraničních prvků podle F.3.3
This is the method used in Example 3 [1]. Nepatrný rozdíl ve využití pochází z rovnice nosníku, která je použita pro stanovení maximálního požadovaného ohybového momentu.
Závěr a výhled
V našem příkladu jsou využití při metodě váženého průměru a přímé pevnostní metodě téměř shodná (0,657 a 0,662). A podle očekávání je metoda hraničních prvků nejkonzervativnější a má nejvyšší využití (0,749).
Databáze znalostí