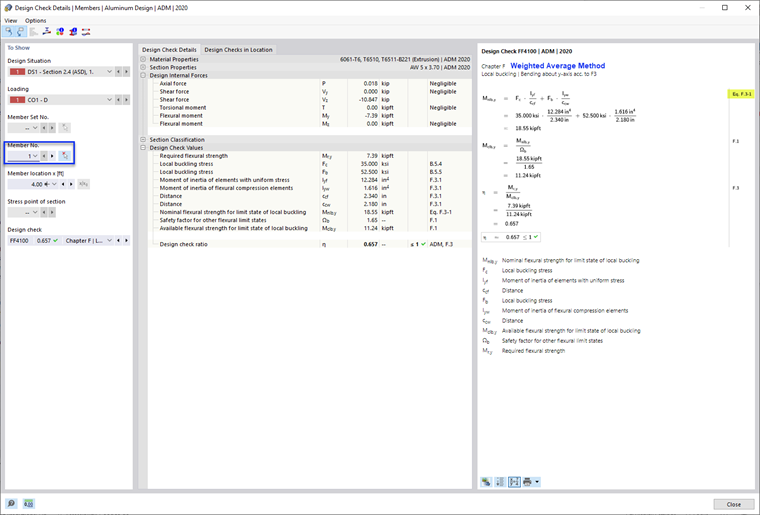
- F.3.1 Metoda średniej ważonej
This is the most common method used in the ADM examples and the default option in RFEM 6. The weighted average method combines strengths determined separately for each element using equation F.3-1 of ADM 2020 <a href="#Refer">[1]</a>.
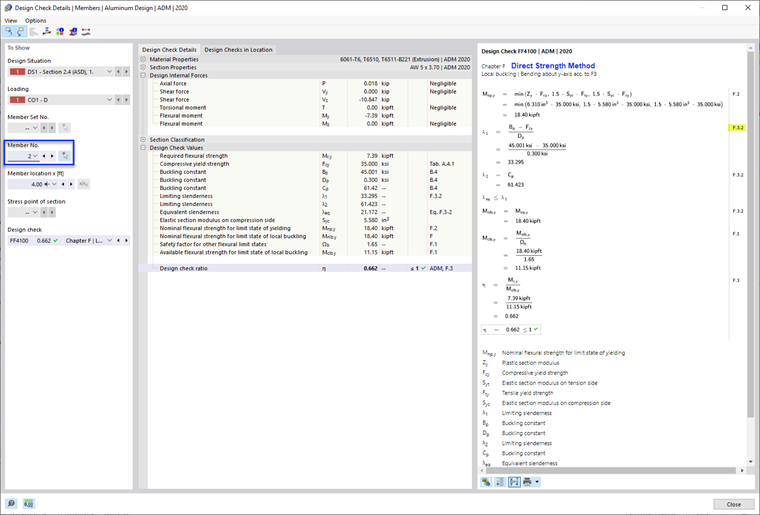
- F.3.2 Direct Strength Method
In this method, the local buckling strength of the cross-section as a whole is determined by analysis which directly includes the interaction of the elements. This method is the most accurate and comprehensive of the three methods.
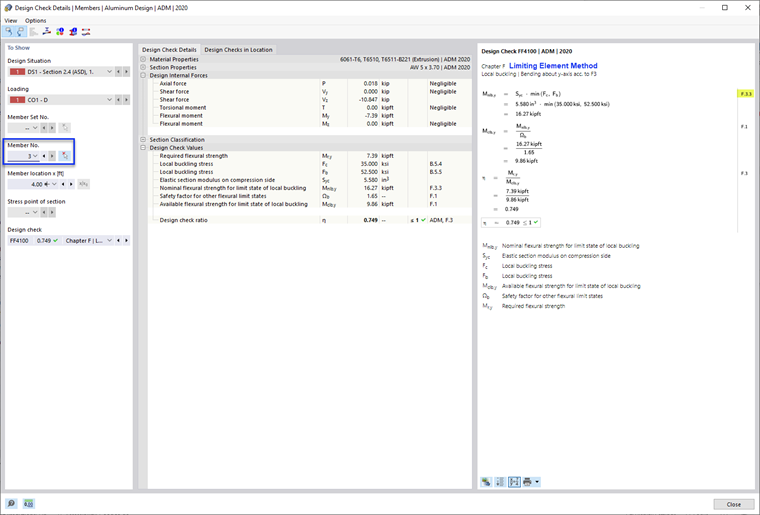
- F.3.3 Limiting Element Method
This method limits the flexural strength of the member based on the lowest local buckling strength of all elements. This method is often less accurate and more conservative, since it does not account for the interaction between elements.
All three methods used in Section F.3 to determine the local buckling strengths reference Sections B.5.4 and B.5.5. These sections include determining the strength of elements in uniform compression and elements in flexural compression. The local buckling strength further depends on whether the element is supported on one or both edges in addition to the width to thickness ratio, b/t.
Comparison of RFEM Results Using the Three Different Methods
The local buckling strength of an aluminum beam in Example 3 of the ADM is compared to the RFEM results using the three different methods described above.
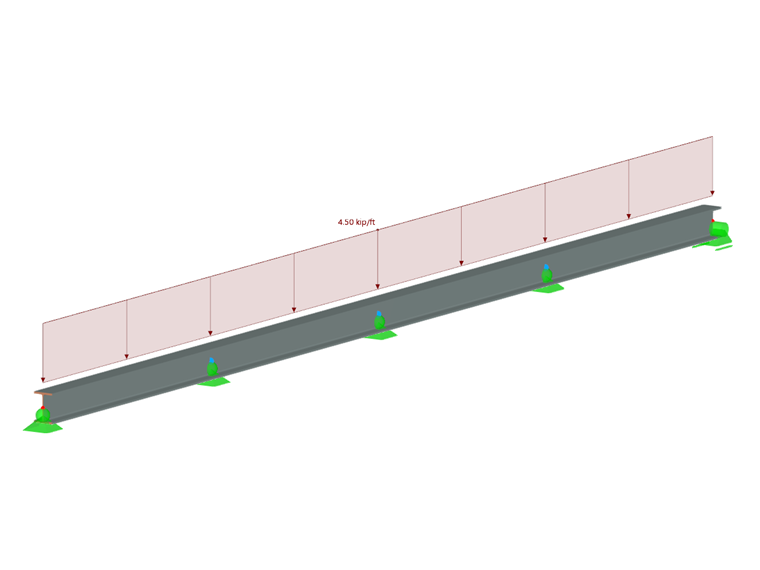
AW 5 x 3.70 section and 6061-T6 (B221) material is used for the 16-foot-long beam. The beam has continuous lateral support and vertical support spacing at 4.0 ft on center. It supports a uniform dead load of 4.50 k/ft (Image 2).
The section properties are shown in Image 3.
.png?mw=760&hash=532a9ec54f1f2d64bc51a71a0a76e52cce2b8524)
The flange and web local buckling stresses are needed to determine the nominal flexural strength of the member.
Flange Local Buckling Stress
The flange (a flat element supported on one edge) is in uniform compression. Its local buckling stress is determined according to Section B.5.4.1.
The slenderness ratio b/t is equal to [(3.5 in -0.19 in - 2*0.30 in)/2] / 0.32 in = 4.234
The slenderness factor λ1 = 6.7 can be found using the equation listed in Section B.5.4.1 or taken directly from Table 2-19 of Part VI.
Since b/t = 4.234 is less than λ1 = 6.7, the yielding limit state controls. Therefore, the uniform compressive stress
Fc = Fcy = 35.0 ksi (Table A.4.1 & Table A.4.3).
Web Local Buckling Stress
The web (a flat element supported on two edges) is in flexural compression. Its local buckling stress is determined according to Section B.5.5.1.
The slenderness ratio b/t is equal to [(5.0 in -2*0.32 in -2*0.3 in)] / 0.19 in = 19.789
The slenderness factor λ1 = 33.1 can be found using the equation listed in Section B.5.5.1 or taken directly from Table 2-19 of Part VI.
Since b/t = 19.789 is less than λ1 = 33.1, the yielding limit state controls. Therefore, the flexural compressive stress, Fb = 1.5*Fcy = 1.5*35.0 ksi = 52.5 ksi (Table A.4.1 & Table A.4.3).
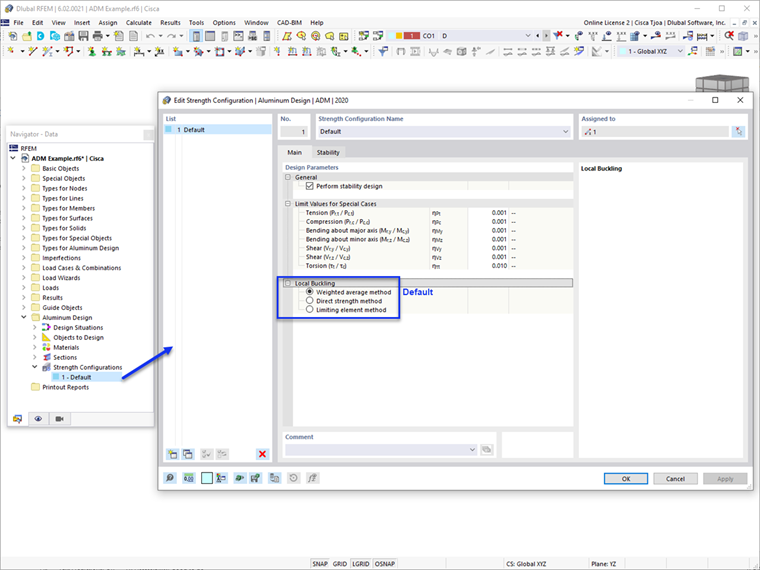
The Design Check Details in RFEM 6 provides the equations and references used in each method. The result output of each method can be verified easily.
- Nominal Flexural Strength, Mnlb as per F.3.1 Weighted Average Method
- Nominal Flexural Strength, Mnlb as per F.3.2 Direct Strength Method
- Nominal Flexural Strength, Mnlb as per F.3.3 Limiting Element Method
This is the method used in Example 3 <a href="#Refer">[1]</a>. The negligible difference in the utilization ratio is from the Beam Formula used to determine the maximum required bending moment.
Uwagi końcowe
In this example, the design check ratios of the Weighted Average Method and Direct Strength Method are almost identical (0.657 and 0.662). And as expected, the Limiting Element Method is the most conservative and has the highest design check ratio (0.749).
303x
6x
Baza informacji
.png?mw=350&hash=316aa4e88ec2f4caa5b692f324d010eab773ec38)
.png?mw=600&hash=49b6a289915d28aa461360f7308b092631b1446e)