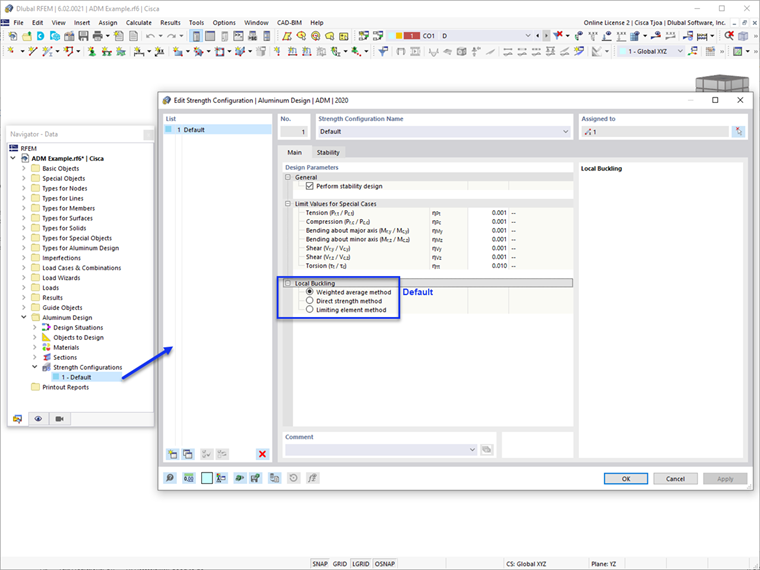
- F.3.1 Méthode de la moyenne pondérée
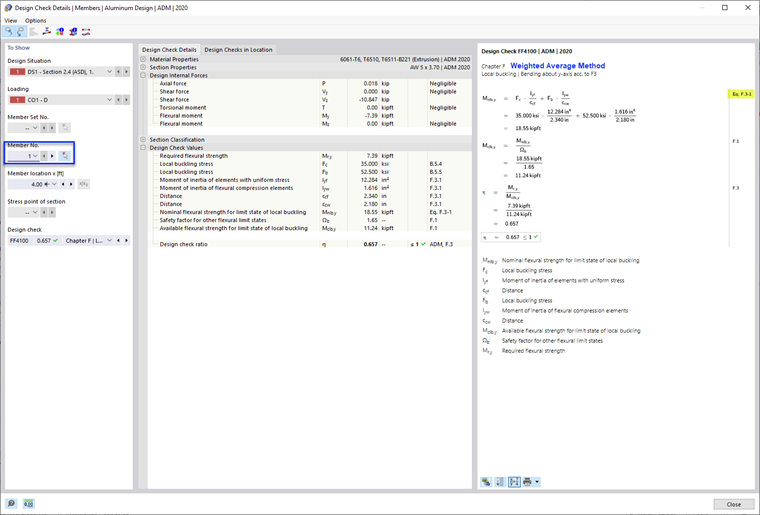
Il s’agit de la méthode la plus couramment utilisée dans les exemples de l’ADM et de l’option par défaut dans RFEM 6. La méthode de la moyenne pondérée combine les résistances déterminées séparément pour chaque élément à l’aide de l’équation F.3-1 de l’ADM 2020 [1].
- F.3.2 Méthode directe de résistance
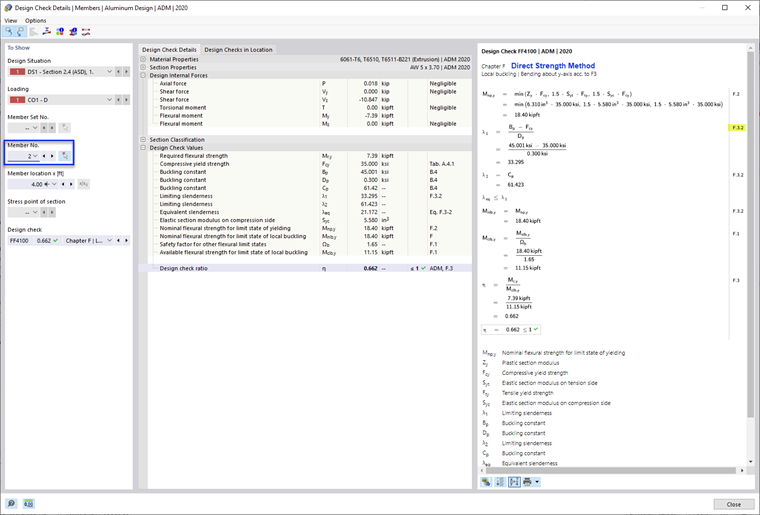
Dans cette méthode, la résistance au flambement local de la section dans son ensemble est déterminée par une analyse qui inclut directement l’interaction des éléments. Cette méthode est la plus précise et la plus complète des trois.
- F.3.3 Méthode de l’élément limite
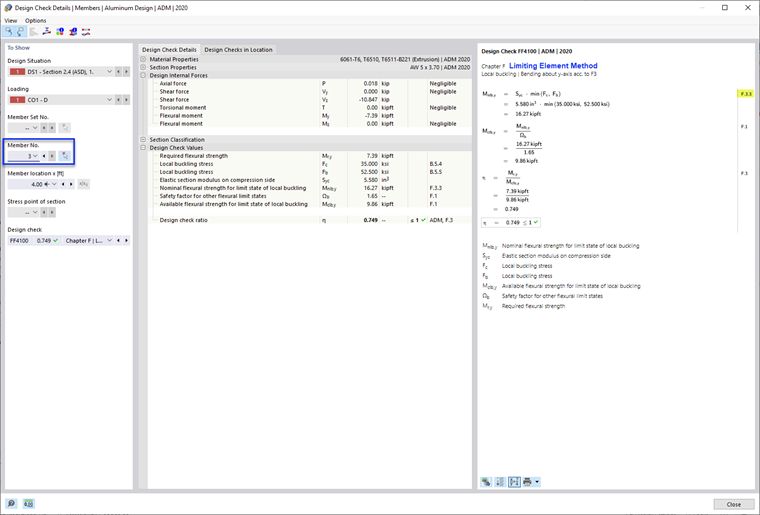
Cette méthode limite la résistance en flexion de la barre en fonction de la résistance au flambement local la plus faible de tous les éléments. Cette méthode est souvent moins précise et plus prudente car elle ne prend pas en compte l’interaction entre les éléments.
Les trois méthodes utilisées dans la clause F.3 pour déterminer les résistances au flambement local font référence aux clauses B.5.4 et B.5.5. Ces clauses comprennent la détermination de la résistance des éléments en compression uniforme et des éléments en compression en flexion. La résistance au flambement local dépend en outre du fait que l’élément repose sur un ou deux bords, ainsi que du rapport largeur/épaisseur b/t.
Comparaison des résultats de RFEM à l’aide de trois méthodes
La résistance au flambement local d’une poutre en aluminium dans l’exemple 3 de l’ADM est comparée aux résultats de RFEM à l’aide des trois méthodes décrites ci-dessus.
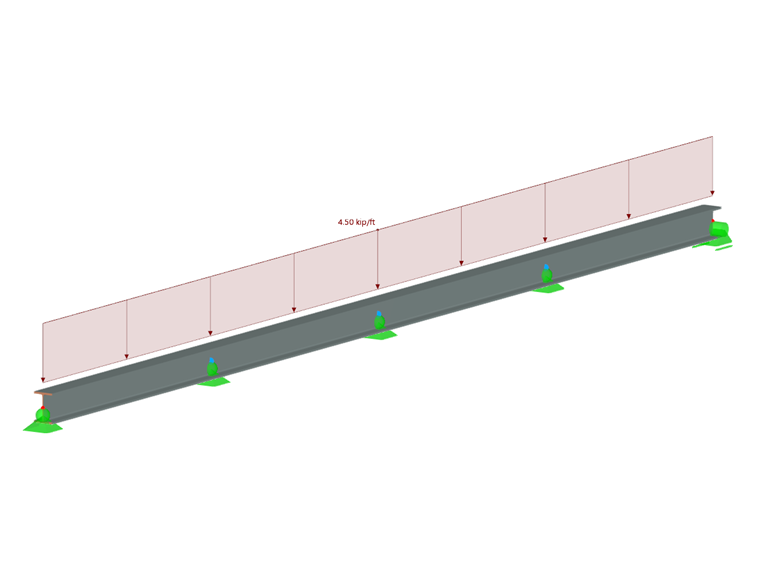
Une section AW 5 x 3,70 et un matériau 6061-T6 (B221) sont utilisés pour la poutre de 4,50 m de long. La poutre a un appui latéral continu et un espacement des appuis verticaux à 1,2 mètres au centre. Elle supporte une charge permanente uniforme de 4,50 k/pi (Figure 2).
Les propriétés de la section sont présentées dans la Figure 3.
.png?mw=760&hash=532a9ec54f1f2d64bc51a71a0a76e52cce2b8524)
Les contraintes de voilement local de la semelle et de l’âme sont nécessaires pour déterminer la résistance nominale en flexion de la barre.
Contrainte de flambement local de la semelle
La semelle (élément plat appuyé sur un bord) est en compression uniforme. Sa contrainte de voilement local est déterminée selon la clause B.5.4.1.
Le rapport d'élancement b/t est égal à [(3,5 in -0,19 in - 2*0,30 in)/2]/0,32 in = 4,234
Le facteur d’élancement λ1 = 6,7 peut être déterminé à l’aide de l’équation de la clause B.5.4.1 ou directement du Tableau 2-19 de la Partie VI.
Étant donné que b/t = 4,234, inférieur à λ1 = 6,7, l’élasticité est l’état limite contrôlé. Par conséquent, la contrainte de compression uniforme
Fc = Fcy = 35,0 ksi (Tableau A.4.1 & Tableau A.4.3).
Contrainte de flambement local de l’âme
L’âme (élément plat reposant sur deux bords) est en compression due à la flexion. Sa contrainte de flambement local est déterminée selon la clause B.5.5.1.
Le rapport d’élancement b/t est égal à [(5,0 in -2*0,32 in -2*0,3 in)] / 0,19 in = 19,789
Le facteur d’élancement λ1 = 33,1 peut être déterminé à l’aide de l’équation de la clause B.5.5.1 ou du Tableau 2-19 de la Partie VI.
Étant donné que b/t = 19,789 est inférieur à λ1 = 33,1, l’élasticité est l’état limite contrôlé. Par conséquent, la contrainte de compression en flexion Fb = 1,5*Fcy = 1,5*35,0 ksi = 52,5 ksi (Tableau A.4.1 & Tableau A.4.3).
Les détails de la vérification dans RFEM 6 fournissent les équations et les références utilisées dans chaque méthode. Les résultats de chaque méthode peuvent être vérifiés facilement.
- Résistance nominale en flexion, Mnlb selon la méthode de la moyenne pondérée F.3.1
- Résistance nominale en flexion, Mnlb selon la méthode de la résistance directe F.3.2
- Résistance nominale en flexion, Mnlb selon la méthode de l’élément limite F.3.3
Il s’agit de la méthode utilisée dans l’exemple 3 [1]. La différence négligeable du rapport d’utilisation provient de la formule de poutre utilisée pour déterminer le moment fléchissant maximal requis.
Conclusion
Dans cet exemple, les rapports de vérification de la méthode de la moyenne pondérée et de la méthode de résistance directe sont presque identiques (0,657 et 0,662). Et comme prévu, la méthode de l’élément limite est la plus prudente et présente le ratio de vérification le plus élevé (0,749).
Base de connaissance
Base de connaissance