В случае тонкостенных стальных элементов, кроме общей потери устойчивости (потеря продольной устойчивости, потеря устойчивости при кручении, поперечная и изгибно-крутильная потеря устойчивости), необходимо также рассчитать характеристики местной устойчивости сечения. В норме EN 1993-1-3 [1] проводится различие между двумя типами:
- Местная потеря продольной устойчивости: характеризуется выпучиванием отдельных частей сечения из их плоскости, при этом углы сечения предполагаются фиксированными шарнирными опорами. Эта форма потери устойчивости описана в норме EN 1993-1-5 [2] как потеря продольной устойчивости пластины.
- Общая потеря устойчивости панели/деформированная потеря устойчивости: характеризуется потерей устойчивости кромочного элемента жесткости сечения. В то же время, деформации в плоскости и из плоскости возникают в смежных частях сечения.
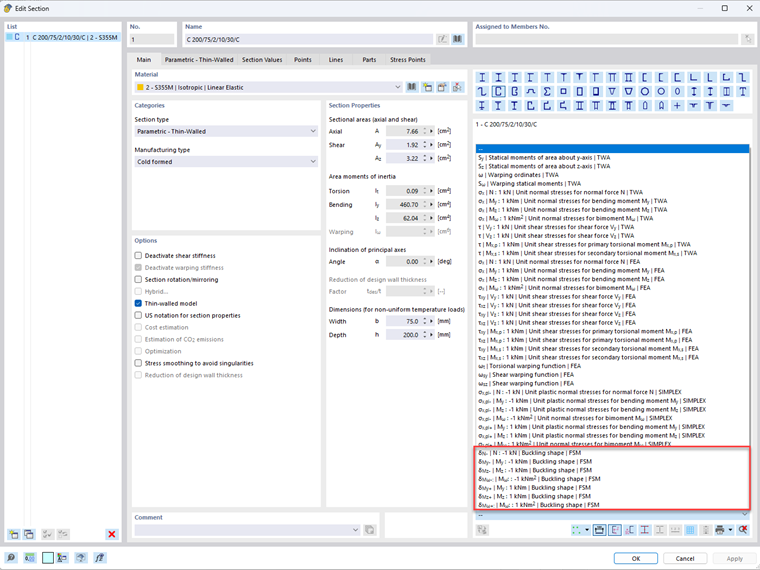
Программы RFEM 6 и RSTAB 9 позволяют рассчитать коэффициенты критической нагрузки и формы колебаний для упомянутых выше явлений местной потери устойчивости с учетом удельной нагрузки. Этот расчет представляет собой линейный расчет на устойчивость, основанный на «ограниченном методе конечных полос (cFSM)» [3]. Результаты расчета методом конечных полос можно легко просмотреть для всех тонкостенных сечений в диалоговом окне «редактировать сечение». Вы можете использовать раскрывающееся меню под значками сечений для выбора формы потери устойчивости из-за удельной нагрузки (рисунок 1) в дополнение к удельным напряжениям и другим функциям сечения.
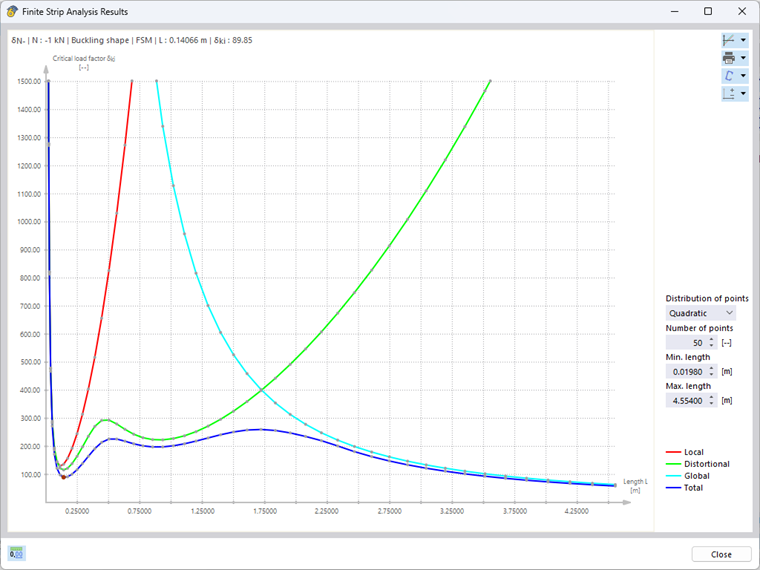
Если выбрать одну из удельных внутренних сил, то откроется интерактивная диаграмма «Результаты метода конечных полос». Графическое изображение синего цвета показывает минимальную критическую нагрузку в качестве функции соответствующей длины полуволны потери устойчивости. Результаты можно отобразить отдельно для различных форм устойчивости, таких как местная потеря устойчивости, деформированная потеря устойчивости и общая потеря устойчивости (для однопролетной балки с вильчатым опиранием) (рисунок 2).
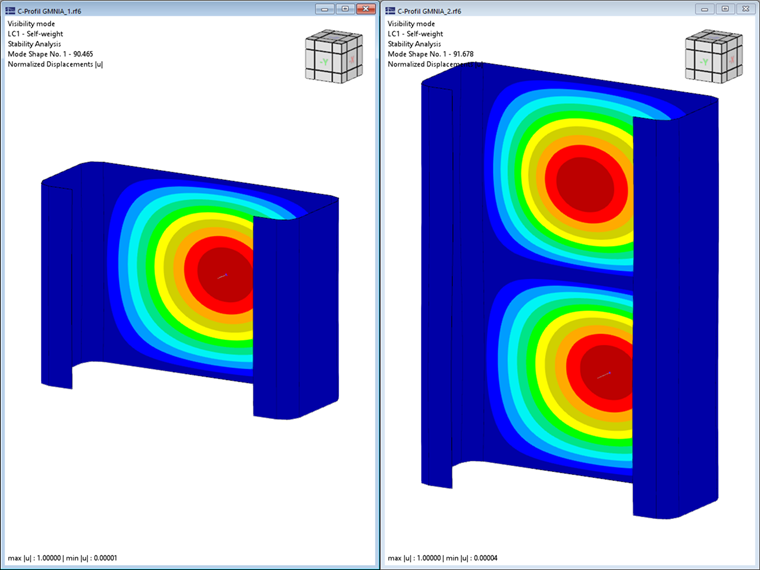
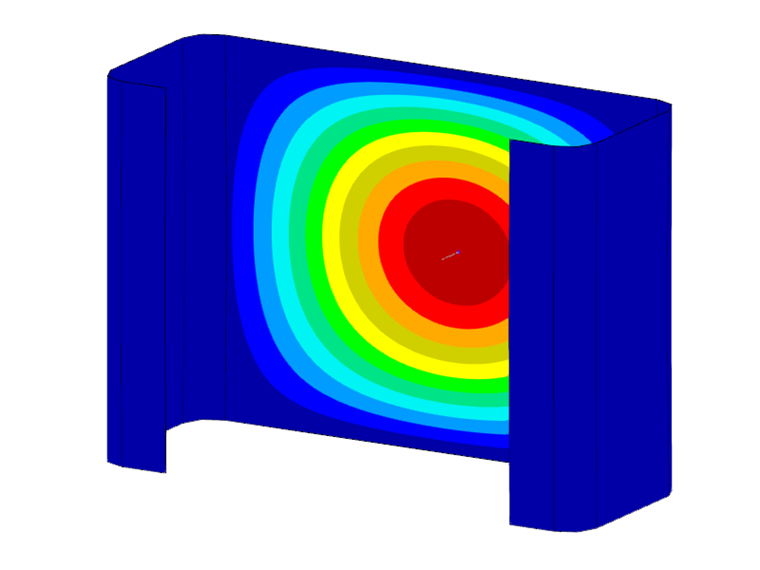
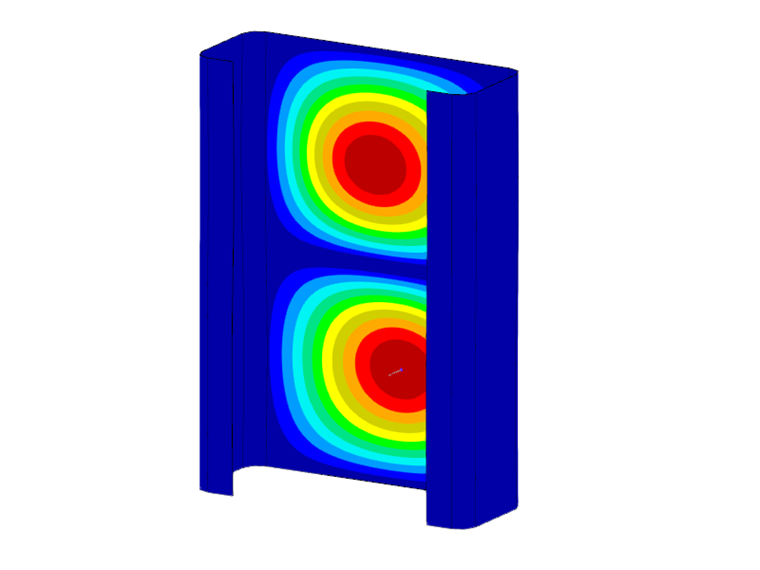
Обратите внимание на то, что при расчете на устойчивость учитывается только первая (одноволновая) форма колебаний соответствующей формы потери устойчивости. При этом установленные критические нагрузки применяются также к кратным соответствующим длинам полуволн. Это можно показать с помощью сравнительного расчета с использованием элементов оболочек и аддона «Устойчивость конструкции». Для данного С-образного профиля длиной 0,141 м мы получим критическую нагрузку -90,47 кН, что полностью соответствует результату FSM -89,85 кН (см. рисунок 2). При удвоении длины до 0,282 м, количество выпучиваний также удваивается при более или менее постоянной критической нагрузке (-91,68 кН). Поэтому при нахождении определяющих критических нагрузок для местной устойчивости (местная потеря устойчивости и деформированная потеря устойчивости) всегда следует учитывать соответствующие минимумы полученных предельных кривых.
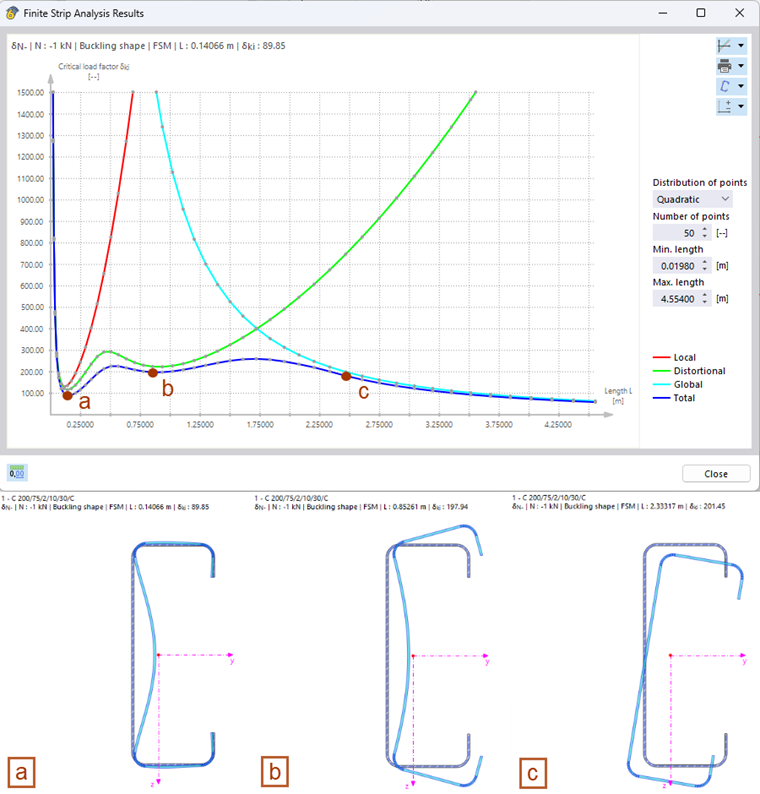
Деформации сечения, связанные с рассчитанной критической нагрузкой, можно увидеть на изображении сечения. По умолчанию отображается собственная форма, которая относится к первому местному минимуму кривой критической нагрузки. При щелчке по любой точке диаграммы, изображение автоматически обновляется. Формы колебаний, показанные на рисунке 4, демонстрируют влияние соответствующих форм устойчивости на найденную критическую нагрузку. В то время как в точке a преобладает местная потеря продольной устойчивости, форма колебаний в точке b характеризуется деформированной потерей устойчивости. Однако в точке c видно движение жёсткого тела сечения, которое связано с общей потерей устойчивости (в данном случае это поперечная и изгибно-крутильная потеря устойчивости).
Результаты МКЭ позволяют выполнить начальную оценку характеристик устойчивости тонких сечений и указывают на то, будет ли потеря устойчивости обусловлена местной, общей или взаимодействием двух форм устойчивости. Кроме того, полученные коэффициенты критической нагрузки могут быть использованы для расчета предельной несущей способности тонких профилей по норме EN 1993-1-3 [1] или AISI S100-16 [4].