Dans le cas de composants en acier à parois minces, outre la rupture de stabilité globale (flambement, flambement par torsion, déversement), le comportement de stabilité locale de la section doit également être examiné. Une distinction est faite entre deux types dans l'EN 1993-1-3 [1] :
- Flambement local : Caractérisé par le flambement des différentes parties de la section hors de leur plan, un appui articulé des coins de la section étant supposé. Ce mode de stabilité est décrit dans l'EN 1993-1-5 [2] comme voilement de plaque.
- Voilement global du panneau/flambement par distorsion : Caractérisé par l'évitement du raidissement de bord d'une section. Dans le même temps, des déformations dans et hors du plan se produisent dans les parties adjacentes de la section.
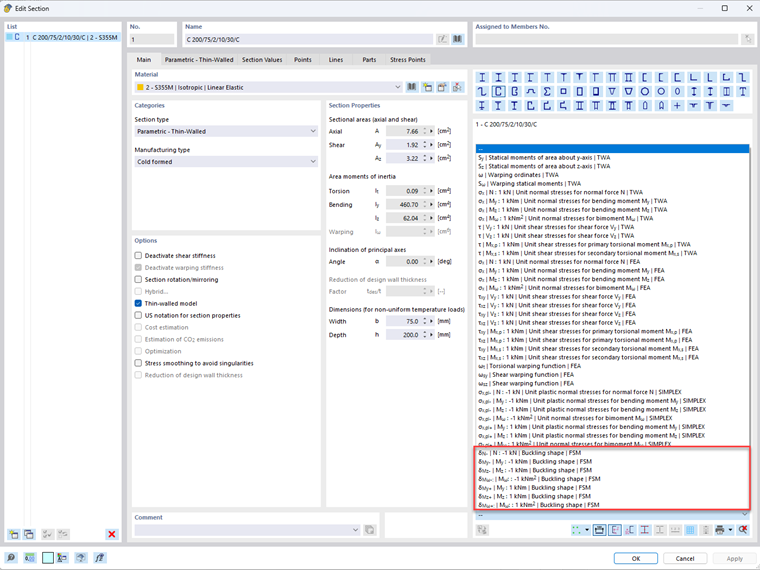
Dans RFEM 6 et RSTAB 9, vous pouvez calculer les facteurs de charge critiques et les modes propres pour les phénomènes de stabilité nommés sous charge unitaire. Le calcul est une analyse de stabilité linéaire basée sur la « Constrained Finite Strip Method (cFSM)" [3]. Les résultats du calcul des bandes finies peuvent être consultés pour toutes les sections à parois minces dans la boîte de dialogue « Modifier les sections ». Outre les contraintes unitaires et d'autres fonctions de section, vous pouvez sélectionner les formes de flambement dû aux contraintes unitaires dans le menu déroulant situé sous l'affichage de la section (Figure 1).
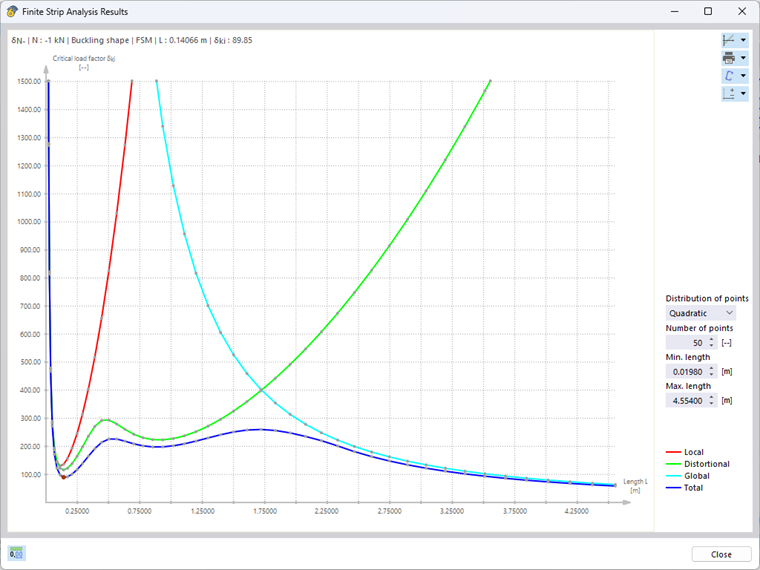
Si l'une des charges unitaires est sélectionnée, le diagramme interactif « Résultats de la méthode des bandes finies » s'ouvre. La courbe en bleu indique la charge critique minimale en fonction de la demi-longueur d'onde de flambement correspondante. Les résultats peuvent également être affichés séparément pour les différents modes de stabilité : flambement local, flambement par distorsion et rupture de stabilité globale (en supposant une poutre à travée simple sur deux appuis) (Figure 2).
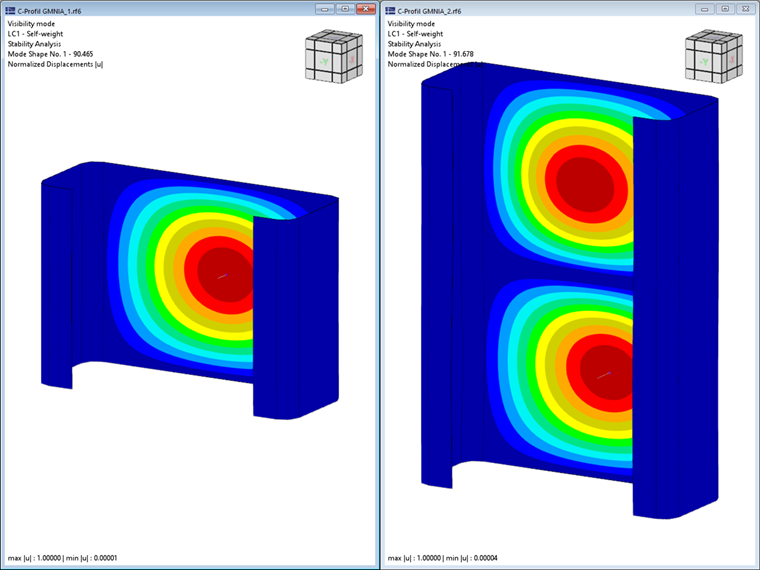
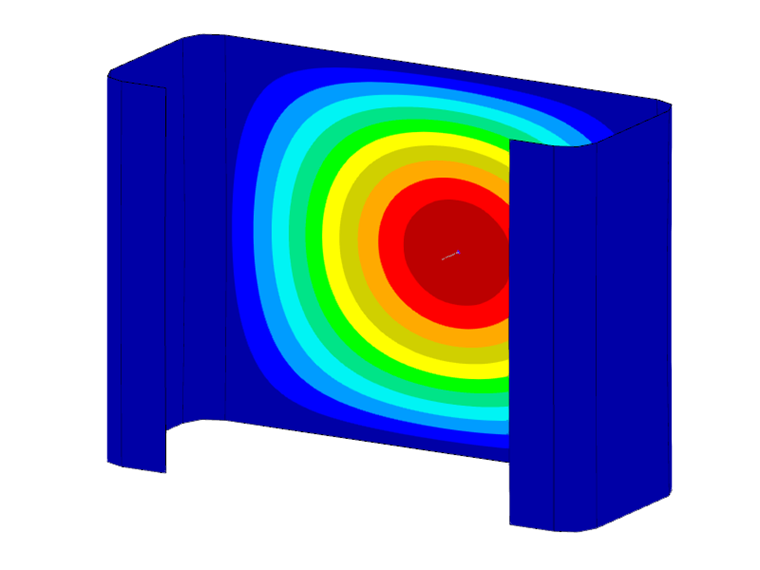
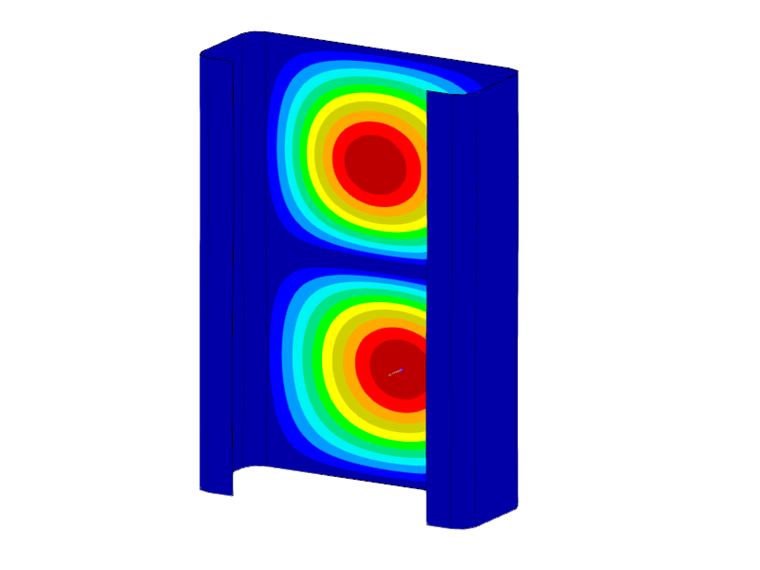
Notez que seul le premier mode propre (onde unique) du mode de stabilité respective est pris en compte dans l'analyse de stabilité. Cependant, les charges critiques déterminées s'appliquent également aux multiples des demi-longueurs d'onde associées. Ceci peut être démontré à l'aide d'un calcul comparatif avec des éléments de coque et le module complémentaire Stabilité de la structure. Pour la section en C étudiée d'une longueur de 0,141 m, cela se traduit par une charge critique de -90,47 kN, ce qui concorde très bien avec le résultat de la méthode des bandes finies de -89,85 kN (voir la Figure 2). Si la longueur est doublée à 0,282 m, le nombre de voilement locaux double également avec une charge critique plus ou moins constante (-91,68 kN). Pour la détermination des charges critiques déterminantes des phénomènes de stabilité locaux (flambement local et flambement par distorsion des sections), les minima respectifs des courbes limites déterminées doivent donc toujours être pris en compte.
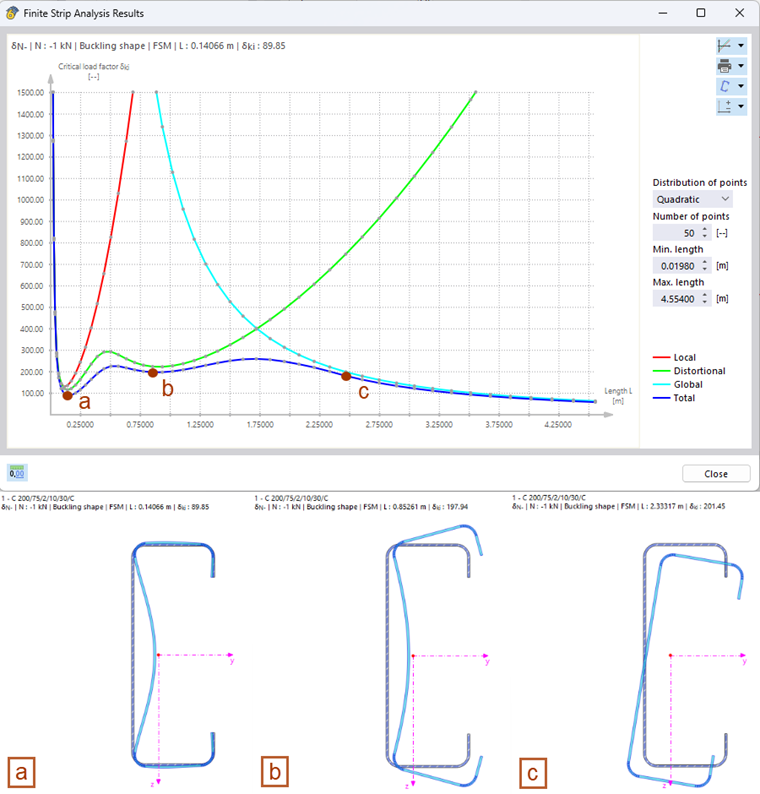
Les déformations de la section associées à une charge critique calculée peuvent être visualisées dans le graphique de la section. Par défaut, le mode propre qui appartient au premier minimum local de la courbe de charge critique est affiché. Cliquer sur n'importe quel point du diagramme met automatiquement à jour l'affichage. Les modes propres représentés à la Figure 4 montrent clairement l'influence des modes de stabilité respectifs sur la charge critique déterminée. Alors que le flambement local domine au point a, le mode propre au point b est caractérisé par un flambement par distorsion des sections. Au point c, en revanche, un mouvement de corps rigide de la section peut être observé, ce qui est associé à la rupture de stabilité globale (ici le déversement).
Les résultats de la méthode des bandes finies permettent une première évaluation du comportement de stabilité des sections élancées et indiquent si la rupture de stabilité est dominée par une interaction locale, globale ou une interaction des deux modes de stabilité. De plus, les facteurs de charge critique déterminés peuvent être utilisés pour calculer la capacité portante ultime des sections élancées selon l’EN 1993-1-3 [1] ou l'AISI S100-16 [4].