Bei dünnwandigen Bauteilen aus Stahl ist neben dem globalen Stabilitätsversagen (Knicken, Drillknicken, Biegedrillknicken) auch das lokale Stabilitätsverhalten des Querschnittes zu untersuchen. Hierbei wird in der EN 1993-1-3 [1] zwischen zwei Arten unterschieden:
- Lokales Beulen: Gekennzeichnet durch das Beulen einzelner Querschnittsteile aus ihrer Ebene wobei eine gelenkige Lagerung der Querschnittsecken angenommen wird. Diese Stabilitätsform wird in der EN 1993-1-5 [2] als Plattenbeulen beschrieben.
- Gesamtfeldbeulen/Forminstabilität: Gekennzeichnet durch das Ausweichen der Randversteifung eines Querschnittes. Gleichzeitig kommt es bei benachbarten Querschnittsteilen zu Verformungen in und aus der Ebene.
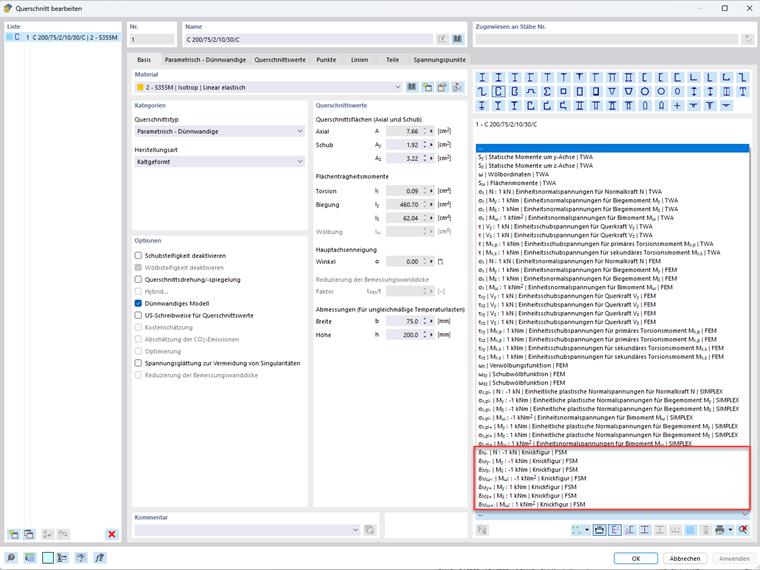
In RFEM 6 und RSTAB 9 lassen sich die Verzweigungslastfaktoren und Eigenformen für die genannten lokalen Stabilitätsphänomene unter Einheitsbeanspruchung berechnen. Es handelt sich bei der Berechnung um eine lineare Stabilitätsanalyse auf Grundlage der „Constrained Finite Strip Method (cFSM)“ [3]. Die Ergebnisse der Finite-Streifen Berechnung sind für alle dünnwandigen Querschnitte im Dialog „Querschnitte bearbeiten“ abrufbar. Über das Dropdown-Menü unterhalb der Querschnittsdarstellung lassen sich neben Einheitsspannungen und weiteren Querschnittsfunktionen die Knickfiguren infolge Einheitsbelastung auswählen (Bild 1).
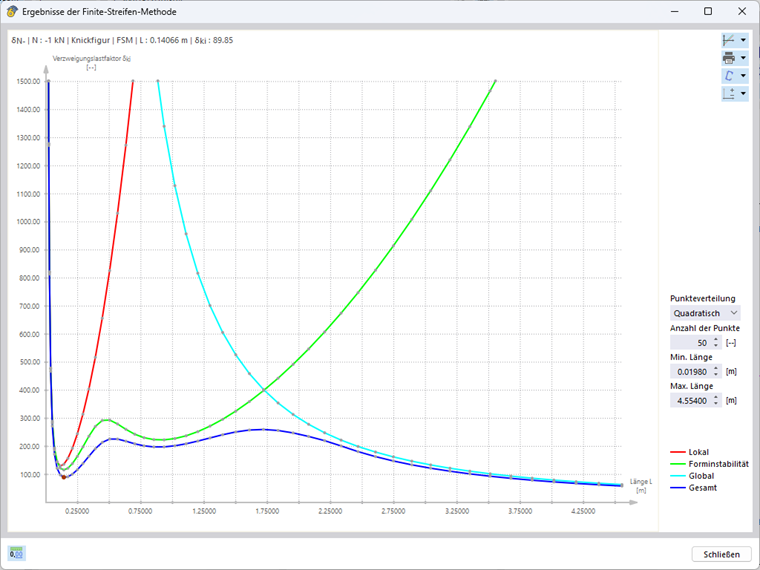
Wird eine der Einheitsbelastungen ausgewählt, öffnet sich das interaktive Diagramm „Ergebnisse der Finite-Streifen-Methode“. Die dargestellte blaue Kurve gibt die minimale Verzweigungslast in Abhängigkeit der zugehörigen Beul-Halbwellenlänge dar. Die Ergebnisse lassen sich auch getrennt für die unterschiedlichen Stabilitätsformen lokales Beulen, Forminstabilität und globales Stabilitätsversagen (bei Annahme eines gabelgelagerten Einfeldträgers) darstellen (Bild 2).
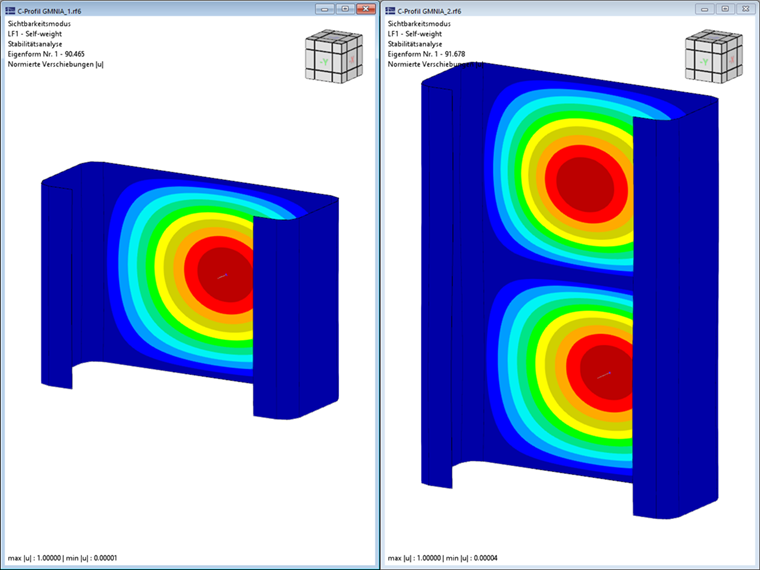
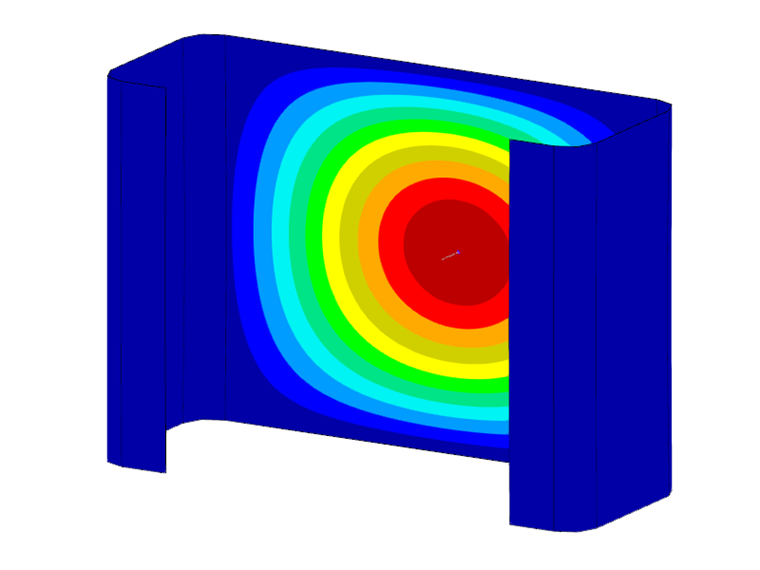
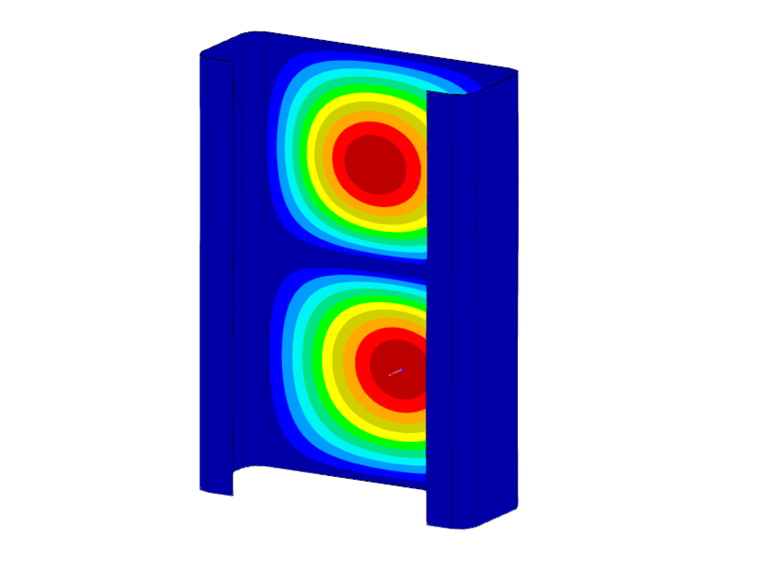
Zu beachten ist, dass nur die erste (einwellige) Eigenform der jeweiligen Stabilitätsform bei der Stabilitätsanalyse berücksichtigt wird. Die ermittelten Verzweigungslasten gelten allerdings auch für Vielfache der zugehörigen Halbwellenlängen. Dies lässt sich anhand einer Vergleichsrechnung mit Schalenelementen und dem Add-on Strukturstabilität zeigen. Für das untersuchte C-Profil mit einer Länge von 0,141 m ergibt sich hier eine Verzweigungslast von -90,47 kN was sehr gut mit dem Ergebnis der FSM von -89,85 kN übereinstimmt (siehe Bild 2). Bei einer Verdoppelung der Länge auf 0,282 m verdoppelt sich auch die Anzahl der Beulen bei mehr oder weniger gleichbleibender Verzweigungslast (-91,68 kN). Für die Ermittlung der maßgebenden Verzweigungslasten der lokalen Stabilitätsphänomene (lokales Beulen und Forminstabilität) sollten daher auf der sicheren Seite stets die jeweiligen Minima der ermittelten Grenzkurven berücksichtigt werden.
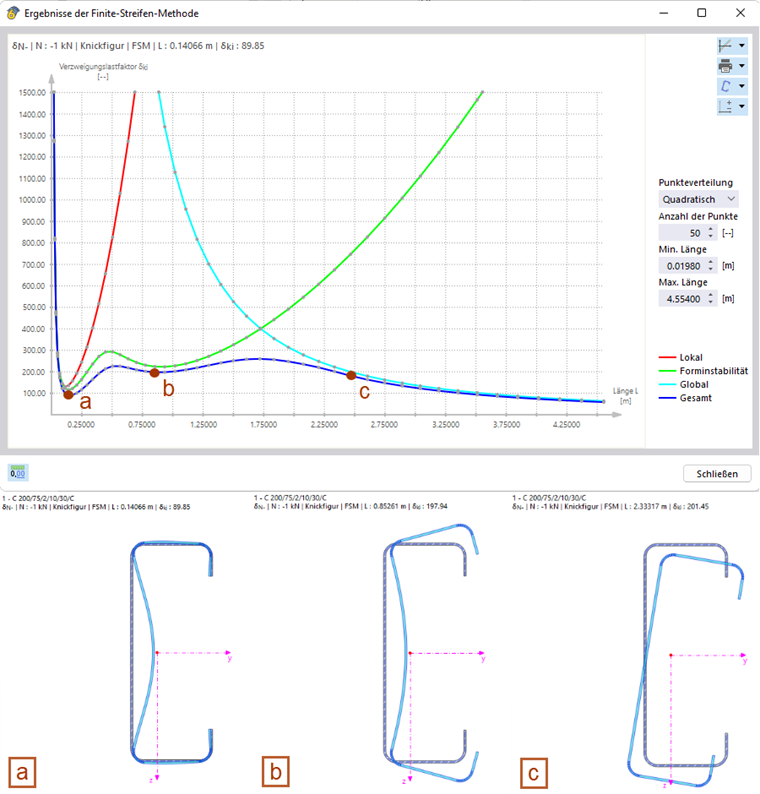
Die Verformungen des Querschnitts, die mit einer berechneten Verzweigungslast einhergehen, können in der Querschnittsgrafik angezeigt werden. Standardmäßig wird die Eigenform, die zum ersten lokalen Minimum der Verzweigungslastkurve gehört, angezeigt. Durch „Anklicken“ eines beliebigen Datenpunktes im Diagramm wird die Darstellung automatisch aktualisiert. Die in Bild 4 gezeigten Eigenformen zeigen eindrücklich den Einfluss der jeweiligen Stabilitätsformen auf die ermittelte Verzweigungslast auf. Während in Punkt a das lokale Beulen dominiert, ist die Eigenform in Punkt b von der Forminstabilität geprägt. In Punkt c ist hingegen eine Starrkörperbewegung des Querschnittes zu erkennen, die mit dem globalen Stabilitätsversagen einhergeht (hier Biegedrillknicken).
Die Ergebnisse der FSM ermöglichen eine erste Bewertung des Stabilitätsverhaltens schlanker Querschnitte und geben einen Hinweis, ob das Stabilitätsversagen durch eine lokale, die globale oder eine Interaktion beider Stabilitätsformen dominiert wird. Die ermittelten Verzweigungslastfaktoren können außerdem verwendet werden, um die Grenztragfähigkeit schlanker Profile gemäß EN 1993-1-3 [1] oder AISI S100-16 [4] zu berechnen.