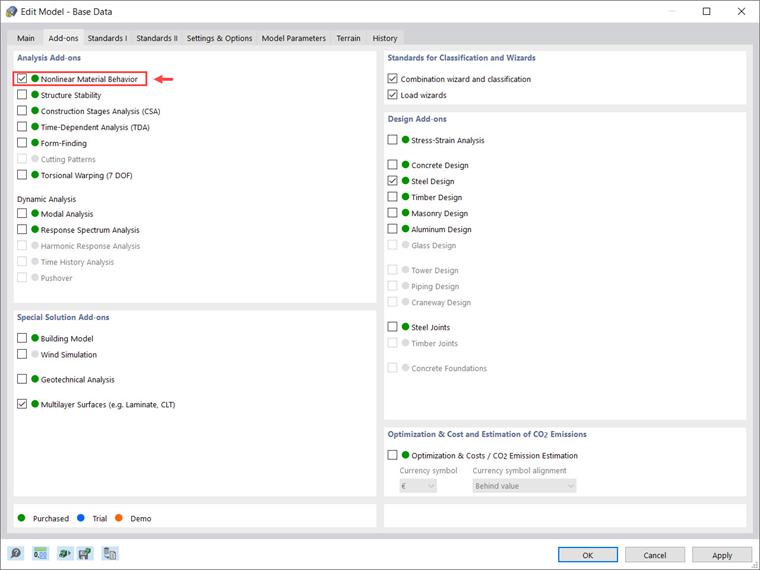
Дополнение "Нелинейное поведение материала" позволяет учитывать материал попадает в RFEM 6. Вы можете активировать это дополнение в Основных данных модели, как показано на Изображении 1.
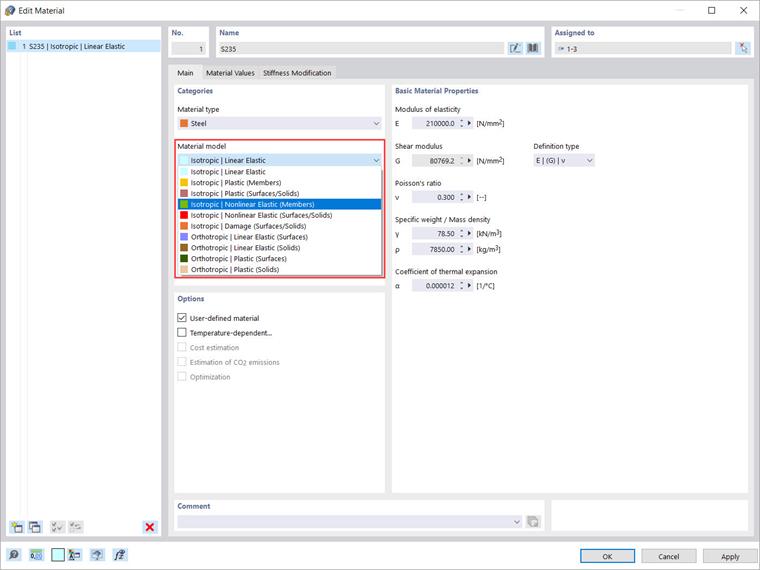
После того как дополнение "Анализ нелинейного поведения материала" активировано, в дополнение к моделям материала «Изотропный | Линейно-упругий» и «Ортотропный | Линейно-упругий» доступны дополнительные опции для выбора в списке (Изображение 2). Таким образом, вы можете выбрать из следующих моделей материала:
- Изотропный | Пластик (Элементы)
- Изотропный | Пластик (Поверхности/Твёрдые тела)
- Изотропный | Нелинейно-упругий (Элементы)
- Изотропный | Нелинейно-упругий (Поверхности/Твёрдые тела)
- Изотропный | Повреждение (Поверхности/Твёрдые тела)
- Ортотропный | Пластик (Поверхности)
- Ортотропный | Пластик (Твёрдые тела)
Изотропный | Пластик (Элементы) Материальная модель
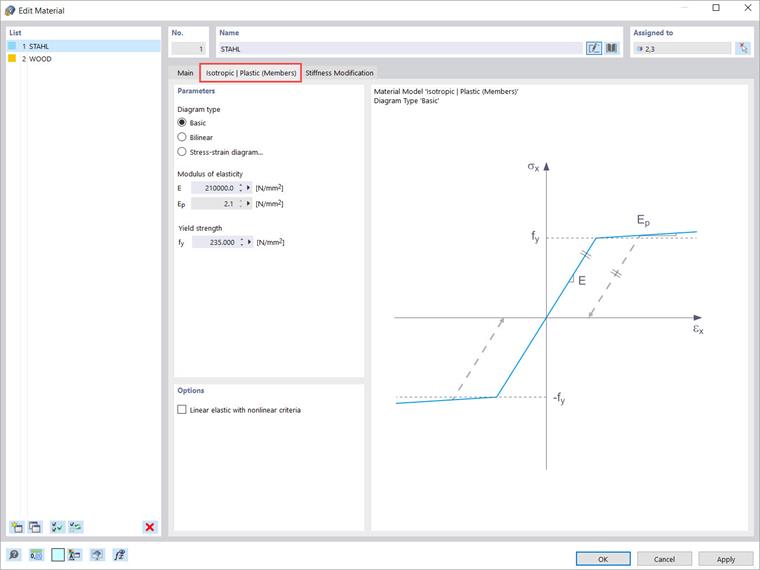
Если вы выберете одну из приведённых выше записей в раскрывающемся списке "Материальная модель", становится доступной новая вкладка для ввода параметров материала. Таким образом, при выборе материальной модели "Изотропный | Пластик (Элементы)" появляется соответствующая вкладка, как показано на Изображении 3.
Во-первых, у вас есть возможность выбрать следующие опции для типа диаграммы:
- Базовый
- Двухлинейный
- Диаграмма напряжение-деформация
Если вы выберете первую опцию (это "Базовый"), программа использует значения из базы данных материалов для модуля упругости E и предела текучести fy. Обратите внимание, что это также двухлинейная материальная модель, в которой ветвь графика не точно горизонтальна по численным причинам и имеет небольшой наклон Ep. В отличие от этого, если диаграмма определена двухлинейно (то есть, выбрана опция "Двухлинейная"), программа позволяет вам ввести значение Ep самостоятельно.
Третья доступная опция (это "Диаграмма напряжение-деформация") позволяет определить более сложные связи между напряжением и деформацией. Обратите внимание, что в этой материальной модели диаграмма напряжение-деформация относится к продольному напряжению σx. Разные точки текучести для сжатия и растяжения не могут учитываться с этой опцией.
Изотропный | Пластик (Поверхности/Твёрдые тела) Материальная модель
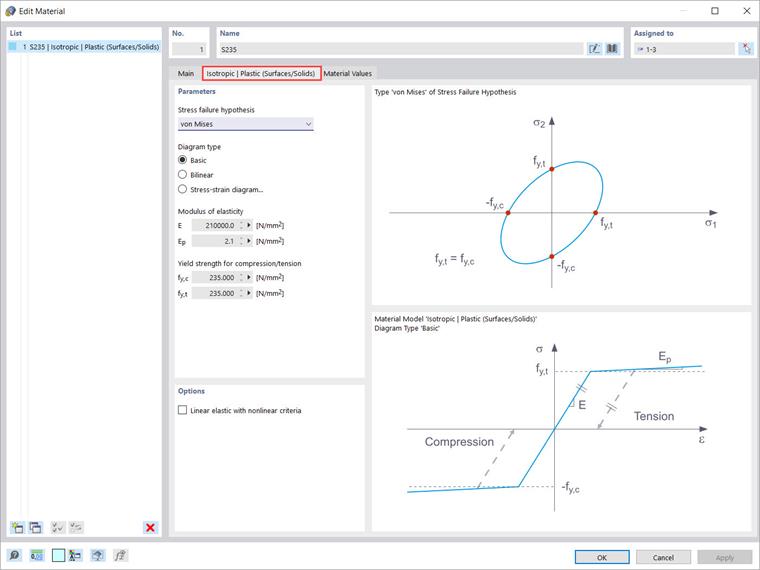
Изотропная пластиковая материальная модель также доступна для поверхностей и твёрдых тел. Таким же образом, как и для модели "Изотропный | Пластик (Элементы)", появляется соответствующая вкладка при выборе записи "Изотропный | Пластик (Поверхности/Твёрдые тела)" в раскрывающемся списке. В дополнение к опциям для определения типа диаграммы (таким же, как для "Изотропный | Пластик (Элементы)"), необходимо выбрать "Гипотеза предела прочности" (Изображение 4).
В раскрывающемся меню доступны следующие гипотезы предела прочности для выбора:
- Мизес
- Треска
- Друкер-Прагер
- Мора-Кулона
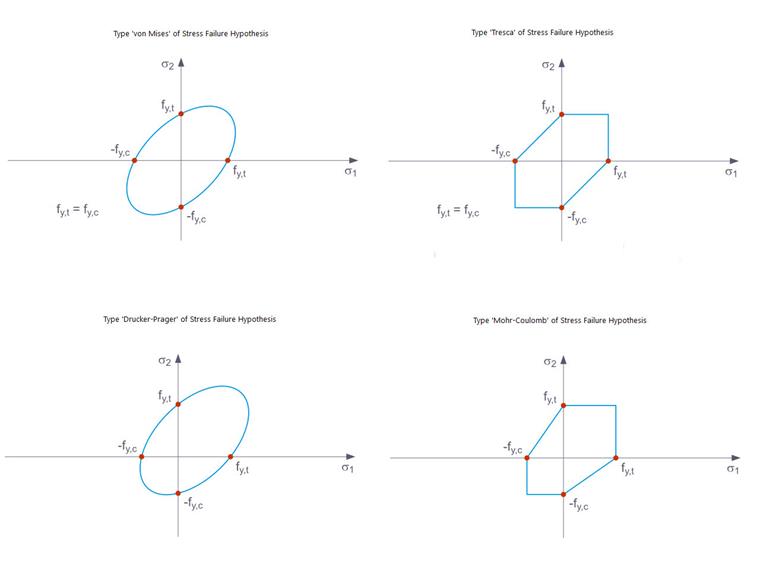
Критерий текучести по Мизесу представляет собой цилиндрическую уравнение с осью гидростатического напряжения в пространстве главных напряжений. Все состояния напряжений в этом пространстве полностью упругие. Состояния напряжений за пределами этого пространства недопустимы. С правилом текучести Треска пластическое деформирование происходит из-за максимального напряжения среза.
В качестве расширения этих критериев текучести есть правила текучести по Друкер-Прагеру и Мору-Кулону, при которых пластическое деформирование происходит, когда максимальное напряжение среза на месте превышается. В первом случае существует поверхность с гладкой границей в пространстве главных напряжений, тогда как во втором - поверхность с недостаточно гладкой границей (Изображение 5).
Изотропный | Нелинейно-упругий (Элементы) Материальная модель
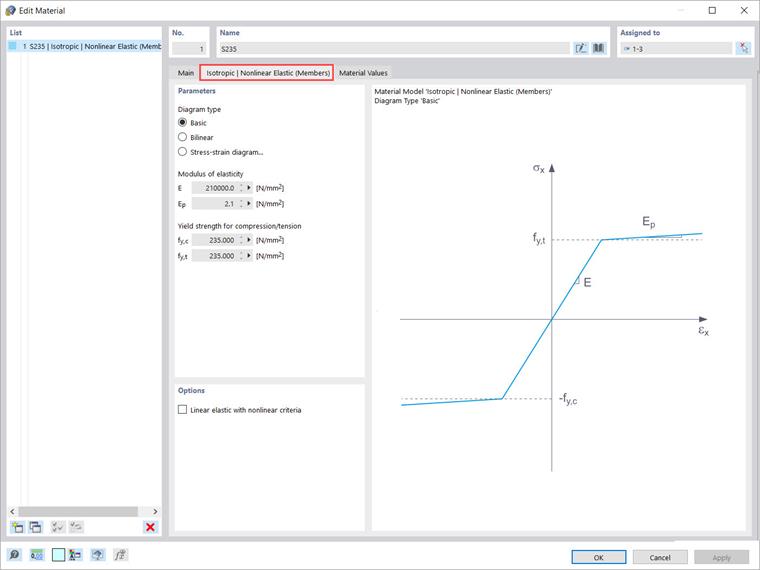
Вкладка для настройки параметров модели "Изотропный | Нелинейно-упругий (Элементы)" очень похожа на вкладку материальной модели "Изотропный | Пластик (Элементы)" (Изображение 6). Фактически, эти модели соответствуют друг другу. Разница между ними связана с общим различием между моделями нелинейной упругой материалов с одной стороны, и пластиковыми моделями с другой стороны.
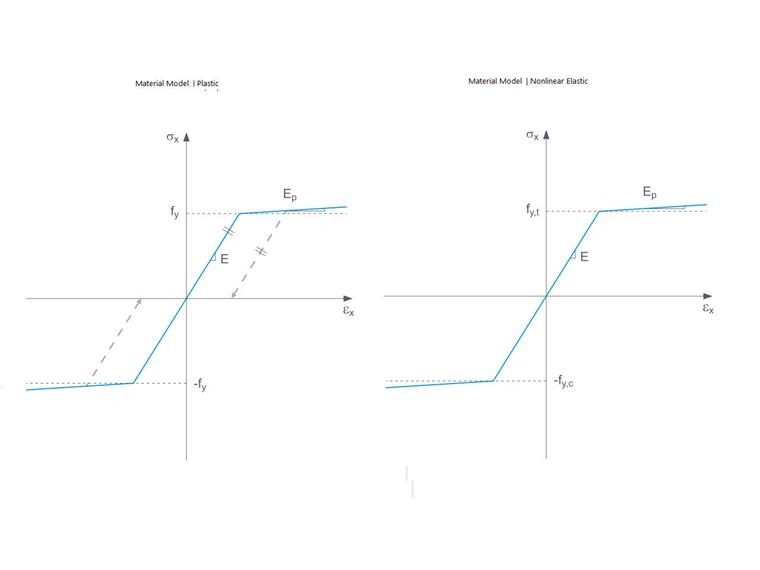
Если структурный элемент с нелинейно-упругим материалом фактически освобождается снова, напряжение возвращается по тому же пути, и больше нет напряжения, когда элемент полностью разгружен. В случае пластиковых материалов, с другой стороны, напряжение остаётся даже после полного снятия нагрузки. Это графически показано на Изображении 7.
Изотропный | Нелинейно-упругий (Поверхности/Твёрдые тела) Материальная модель
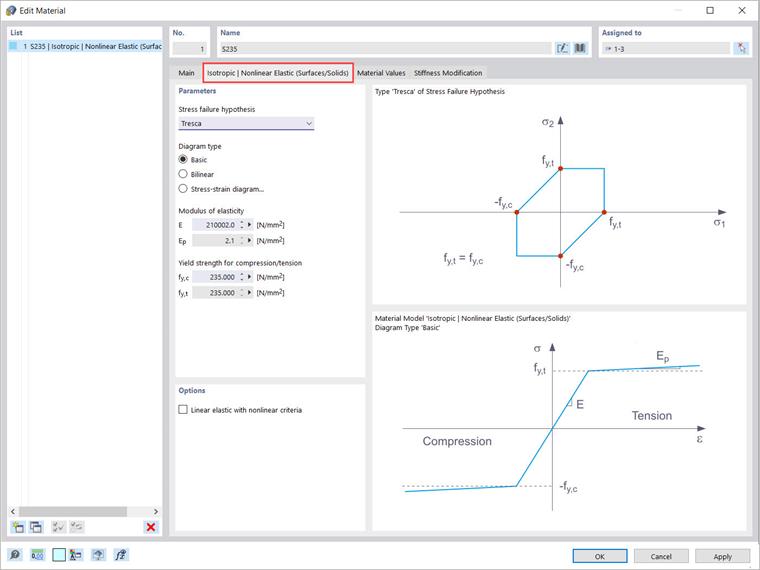
Та же дискуссия применима к соответствию между моделями материалов "Изотропный | Пластик (Поверхности/Твёрдые тела)" и "Изотропный | Нелинейно-упругий (Поверхности/Твёрдые тела)". Свойства модели должны быть определены так же (Изображение 8), с разницей, что после удаления нагрузки остаётся никакая пластическая деформация.
Изотропный | Повреждение (Поверхности/Твёрдые тела) Материальная модель
Указанные ранее законы текучести ограничены поверхностью текучести в пространстве главных напряжений, и их правила текучести могут применяться только к чисто упруго-пластическому поведению материала. Однако многие материалы не демонстрируют чисто симметричного нелинейного поведения. Для моделирования поведения материалов, подвергающихся процессу повреждения из-за трещин, требуется более подходящая материальная модель. Такой материал - это бетон, который имеет значительно более высокую прочность на сжатие, чем на растяжение.
Трещины, возникающие в зоне растяжения материала, снижают жесткость системы. В случае железобетона или армированного волокнами бетона, арматура поглощает растягивающие напряжения.
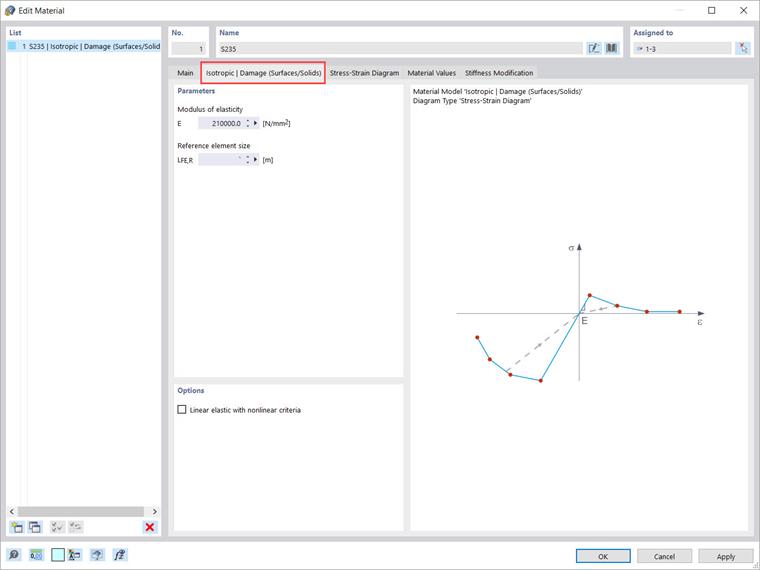
Для моделирования поведения таких материалов (например, стального волокнистого бетона), RFEM 6 предлагает вам материальную модель "Изотропный | Повреждение (Поверхности/Твёрдые тела)". Если вы выберете эту материальную модель, вам доступна вкладка, показанная на Изображении 9, для определения параметров модели.
В отличие от других моделей материалов, диаграмма напряжение-деформация для этой модели материалов не антиметрична относительно начала координат. "Референсный размер элемента" контролирует, как напряжение в области трещин масштабируется по длине элемента. При значении по умолчанию ноль, масштабирование не выполняется. В результате поведение материала стального волокнистого бетона моделируется реалистично.
Ортотропный | Пластик (Поверхности, Твёрдые тела) | Tsai-Wu Материальная модель
С ортотропной пластиковой материальной моделью для поверхностей и твёрдых тел в RFEM 6, поверхности и твёрдые тела с пластиковыми свойствами материалов могут быть рассчитаны и оценены согласно критерию разрушения Tsai-Wu. Эта материальная модель сочетает пластиковые и ортотропные свойства, что позволяет особое моделирование материалов с анизотропными свойствами. Таким образом, эта материальная модель может использоваться для представления поведения пластмасс, армированных волокнами, или древесно-стружечных плит.
В этой материальной модели эластичный диапазон соответствует материальной модели "Ортотропный | Линейно-упругий (Твёрдые тела)", тогда как для пластического диапазона применяются текучести согласно Tsai-Wu. Изображение 10 показывает условия текучести для обеих поверхностей (2D) и твёрдых тел (3D).
Если значение fy(σ) согласно уравнению Tsai-Wu, плоское напряженное состояние, меньше 1, напряжения находятся в области эластичности. Пластическая область достигается, как только fy(σ) = 1. Значения выше 1 не допускаются. Поведение модели идеально пластично; то есть, отсутствует упрочнение.
Резюме
Дополнение "Нелинейное поведение материала" позволяет учитывать материальные нелинейности в RFEM 6. Если вы активируете это дополнение в Основных данных модели, список материальных моделей расширяется, и вы можете легко выбрать интересующую вас нелинейную материальную модель.
При работе с нелинейными материальными моделями программа всегда выполняет итерационный расчёт. В зависимости от выбранной модели определяется различная связь между напряжениями и деформациями. Жесткость конечных элементов постоянно регулируется в ходе итераций, пока не будет удовлетворена связь напряжение-деформация.
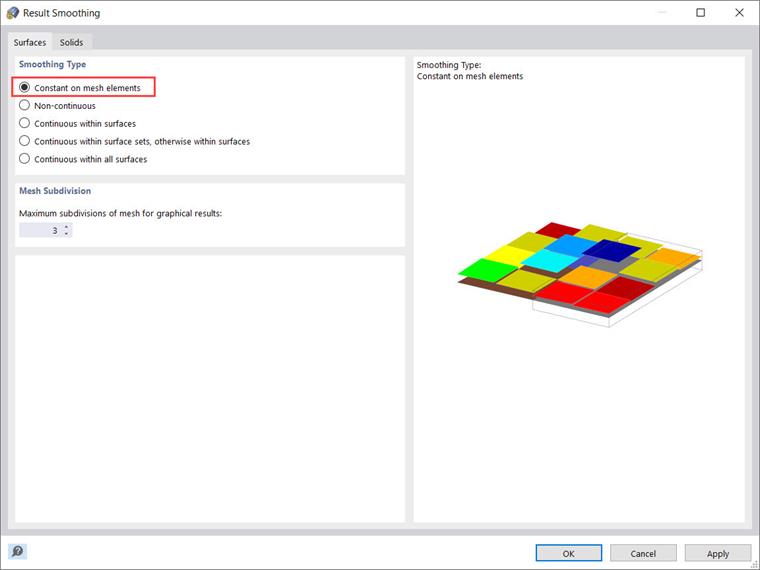
Регулировка всегда выполняется для всей поверхности или твердого элемента. Поэтому рекомендуется всегда использовать тип сглаживания "Постоянно на ячейках сетки" при оценке напряжений, как показано на Изображении 11.