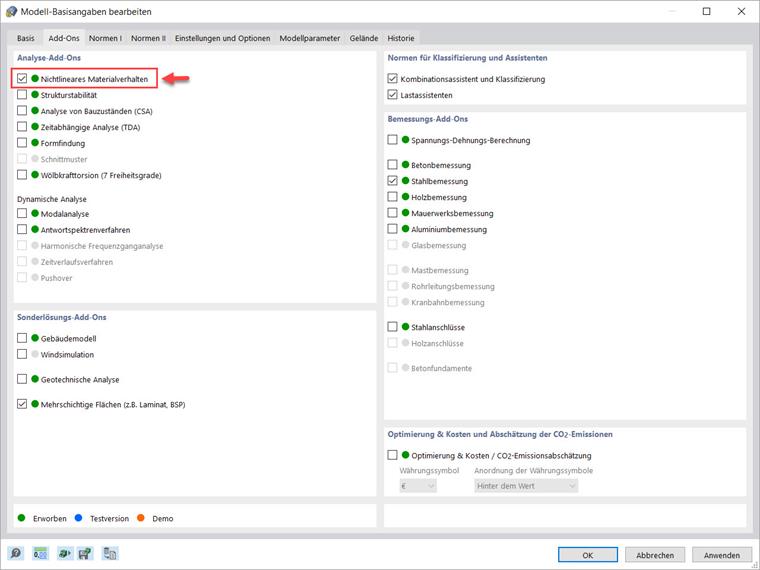
Das Add-On 'Nichtlineares Materialverhalten' ermöglicht es Ihnen, Materialnichtlinearitäten in RFEM 6 zu berücksichtigen. Sie können dieses Add-On in den Basisangaben des Modells aktivieren, wie in Bild 1 gezeigt.
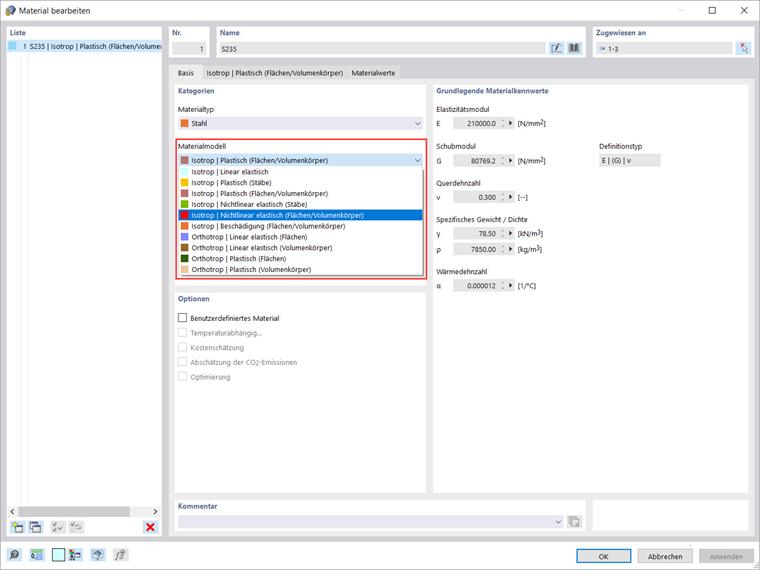
Sobald das Analyse-Add-On 'Nichtlineares Materialverhalten' aktiviert ist, stehen zusätzlich zu den Materialmodellen „Isotrop | Linear elastisch“ und „Orthotrop | Linear elastisch“ in der Liste weitere Optionen zur Auswahl zur Verfügung (Bild 2). Sie können daher zwischen den folgenden Materialmodellen wählen:
- Isotrop | Plastisch (Stäbe)
- Isotrop | Plastisch (Flächen/Volumenkörper)
- Isotrop | Nichtlinear elastisch (Stäbe)
- Isotrop | Nichtlinear elastisch (Flächen/Volumenkörper)
- Isotrop | Beschädigung (Flächen/Volumenkörper)
- Orthotrop | Plastisch (Flächen)
- Orthotrop | Plastisch (Volumenkörper)
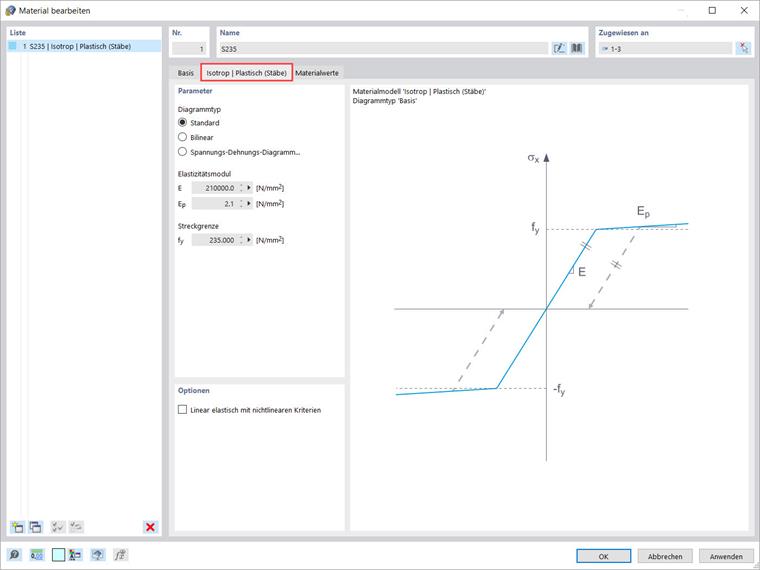
Materialmodell 'Isotrop | Plastisch (Stäbe)'
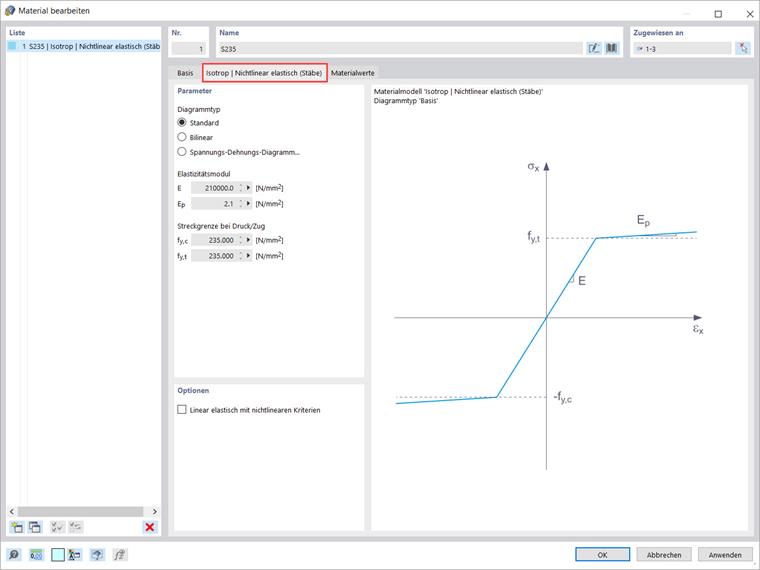
Wenn Sie einen der oben genannten Einträge in der Dropdown-Liste „Materialmodell“ auswählen, steht ein neues Register zur Eingabe der Materialparameter zur Verfügung. Wenn Sie also das Materialmodell „Isotrop | Plastisch (Stäbe)“ auswählen, erscheint ein entsprechender Reiter, wie in Bild 3 dargestellt.
Zuerst haben Sie die Möglichkeit, die folgenden Optionen für den Diagrammtyp auszuwählen:
- Standard
- Bilinear
- Spannungs-Dehnungs-Diagramm
Wenn Sie die erste Option (also „Standard“) wählen, verwendet das Programm Werte aus der Materialdatenbank für den Elastizitätsmodul E und die Streckgrenze fy. Bitte beachten Sie, dass es sich hierbei ebenfalls um ein bilineares Materialmodell handelt, bei dem der Ast des Graphen aus numerischen Gründen nicht exakt horizontal verläuft und eine geringe Steigung Ep aufweist. Wenn das Diagramm hingegen bilinear definiert ist (d.h. die Option „Bilinear“), ermöglicht es Ihnen das Programm, den Wert von Ep selbst einzugeben.
Die dritte verfügbare Option („Spannungs-Dehnungs-Diagramm“) ermöglicht es Ihnen, komplexere Beziehungen zwischen Spannung und Dehnung zu definieren. Bitte beachten Sie, dass das Spannungs-Dehnungs-Diagramm in diesem Materialmodell auf die Längsspannung σx bezogen ist. Verschiedene Fließgrenzen für Zug und Druck können mit dieser Option nicht berücksichtigt werden.
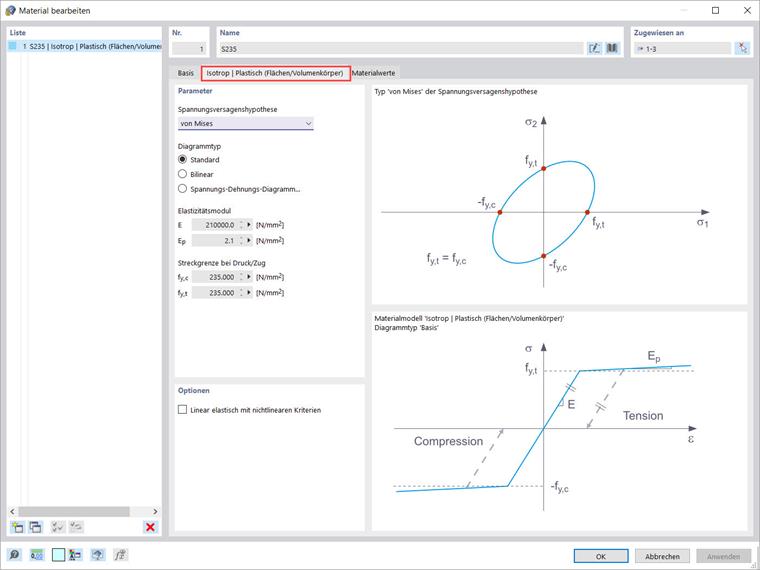
Materialmodell 'Isotrop | Plastisch (Flächen/Volumenkörper)'
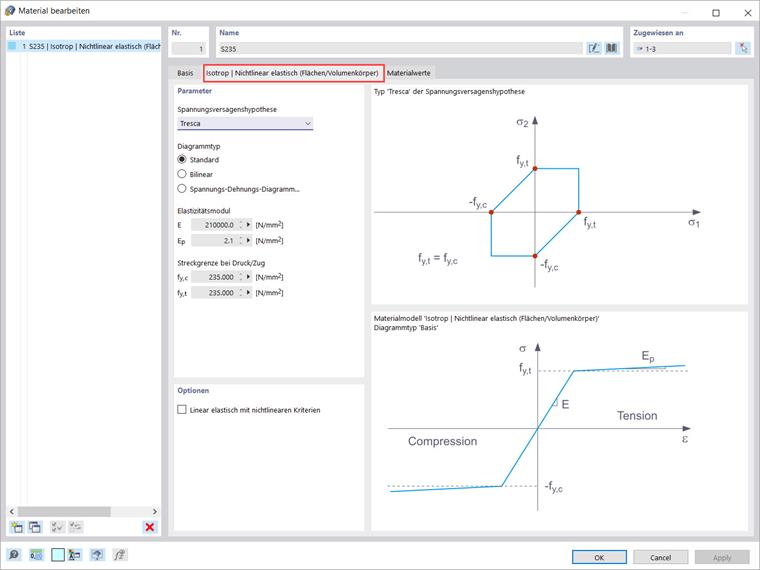
Das isotrope plastische Materialmodell ist auch für Flächen und Volumenkörper verfügbar. Ebenso wie für das Modell „Isotrop | Plastisch (Stäbe)“ erscheint ein entsprechendes Register, wenn „Isotrop | Plastisch (Flächen/Volumenkörper)“ in der Dropdown-Liste ausgewählt wird. Zusätzlich zu den Optionen zur Definition des Diagrammtyps (gleich wie für „Isotrop | Plastisch (Stäbe)“) muss die „Spannungsversagenshypothese“ ausgewählt werden (Bild 4).
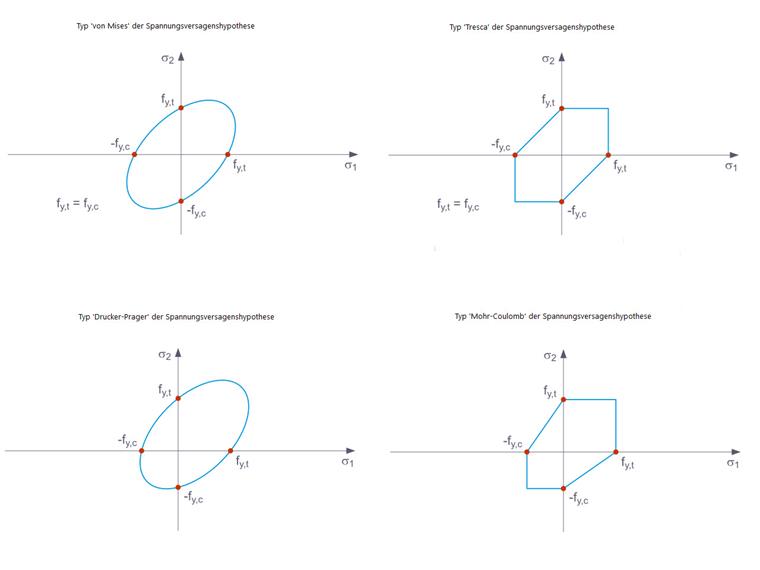
Die folgenden Spannungsversagenshypothesen stehen in der Dropdown-Liste zur Auswahl:
- von Mises
- Tresca
- Drucker-Prager
- Mohr-Coulomb
Das Fließkriterium nach von Mises ist ein Kreiszylinder mit hydrostatischer Achse im Hauptspannungsraum. Alle Spannungszustände innerhalb dieses Raums sind vollständig elastisch. Spannungszustände außerhalb dieses Raums sind nicht zulässig. Bei der Tresca’schen Fließregel tritt das plastische Fließen aufgrund der maximalen Schubspannung auf.
Als Erweiterung dieser Fließkriterien gibt es die Fließregeln nach Drucker-Prager und Mohr-Coulomb, bei denen das plastische Fließen eintritt, wenn die maximale Schubspannung lokal überschritten wird. Bei ersterem gibt es eine Oberfläche mit glattem Rand im Hauptspannungsraum, während letzterer eine Oberfläche mit nicht glattem Rand ist (Bild 5).
Materialmodell 'Isotrop | Nichtlinear elastisch (Stäbe)'
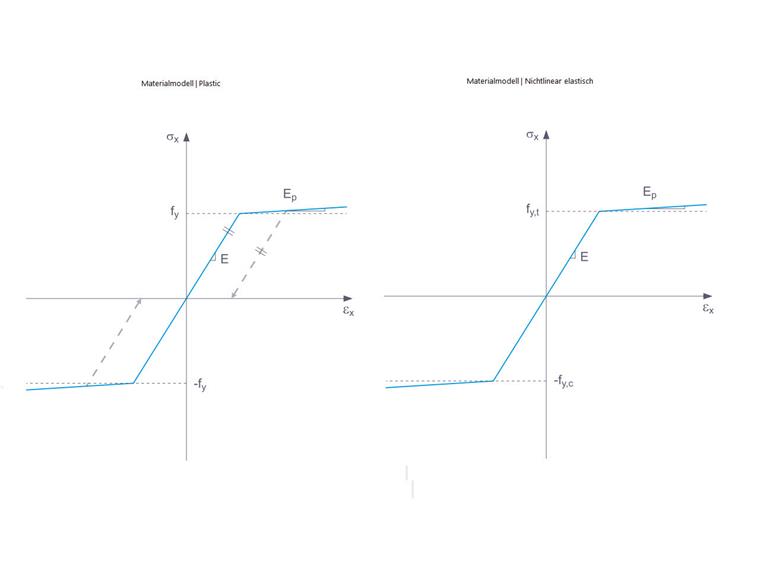
Der Reiter zur Einstellung der Parameter des Modells „Isotrop | Nichtlinear elastisch (Stäbe)“ ist dem des Materialmodells „Isotrop | Plastisch (Stäbe)“ sehr ähnlich (Bild 6). Tatsächlich stimmen diese Modelle miteinander überein. Der Unterschied zwischen ihnen hängt mit der allgemeinen Unterscheidung zwischen den Modellen für nichtlineare elastische Materialien einerseits und den Modellen für plastische Materialien andererseits zusammen.
Wenn ein Bauteil aus einem nichtlinearen elastischen Material tatsächlich wieder freigegeben wird, kehrt die Dehnung auf dem gleichen Weg zurück und es liegt keine Dehnung mehr vor, wenn das Bauteil vollständig entlastet ist. Bei plastischen Materialien hingegen bleibt die Dehnung auch nach vollständiger Entlastung bestehen. Dies ist in Bild 7 grafisch dargestellt.
Materialmodell 'Isotrop | Nichtlinear elastisch (Flächen/Volumenkörper)'
Die gleiche Überlegung gilt für die Entsprechung zwischen den Materialmodellen „Isotrop | Plastisch (Flächen/Volumenkörper)“ und „Isotrop | Nichtlinear elastisch (Flächen/Volumenkörper)“. Die Eigenschaften des Modells sollten auf die gleiche Weise definiert werden (Bild 8), mit dem Unterschied, dass nach der Belastungsentfernung keine plastische Dehnung verbleibt.
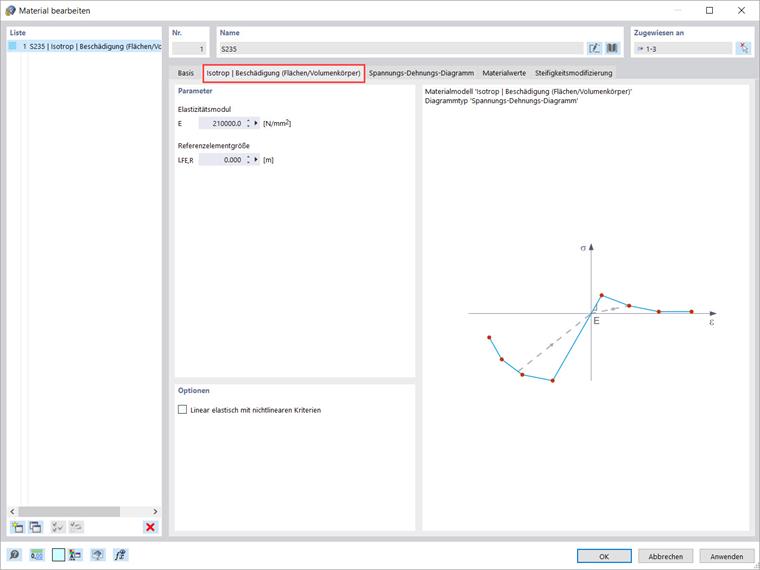
Materialmodell 'Isotrop | Beschädigung (Flächen/Volumenkörper)'
Die zuvor im Artikel erwähnten Fließgesetze beschränken sich auf die Fließfläche im Hauptspannungsraum und ihre Fließregeln können nur auf rein elastisch-plastisches Materialverhalten angewendet werden. Viele Materialien weisen jedoch kein rein symmetrisches nichtlineares Verhalten auf. Um das Verhalten von Materialien zu simulieren, die einem durch Risse verursachten Beschädigungsprozess ausgesetzt sind, ist ein geeigneteres Materialmodell erforderlich. Ein solches Material ist Beton, der eine deutlich höhere Druckfestigkeit als Zugfestigkeit aufweist.
Die Risse, die im Zugbereich des Materials auftreten, verringern die Steifigkeit des Systems. Bei Stahlbeton oder faserverstärktem Beton nimmt die Bewehrung die Zugspannungen auf.
Um das Verhalten solcher Materialien (zum Beispiel stahlfaserverstärkter Beton) zu simulieren, bietet RFEM 6 das Materialmodell „Isotrop | Beschädigung (Flächen/Volumenkörper)“. Wenn Sie dieses Materialmodell auswählen, steht Ihnen das in Bild 9 gezeigte Register zur Definition der Modellparameter zur Verfügung.
Im Gegensatz zu anderen Materialmodellen ist das Spannungs-Dehnungs-Diagramm für dieses Materialmodell nicht antimetrisch zum Ursprung. Die „Referenzelementgröße“ steuert, wie die Dehnung im Rissbereich auf die Länge des Elements skaliert wird. Mit dem Standardwert Null wird keine Skalierung durchgeführt. Dadurch wird das Materialverhalten des stahlfaserverstärkten Betons realistisch modelliert.
Materialmodell 'Orthotrop | Plastisch (Flächen, Volumenkörper) | Tsai-Wu'
Mit dem orthotropen plastischen Materialmodell für Flächen und Volumenkörper in RFEM 6 können Flächen und Volumen mit plastischen Materialeigenschaften nach dem Tsai-Wu-Ausfallkriterium berechnet und auswertet werden. Dieses Materialmodell kombiniert plastische und orthotrope Eigenschaften, wodurch eine spezielle Modellierung von Materialien mit anisotropen Eigenschaften ermöglicht wird. Dieses Materialmodell kann somit zur Darstellung des Verhaltens von faserverstärkten Kunststoffen oder Holzwerkstoffen verwendet werden.
In diesem Materialmodell entspricht der elastische Bereich dem Materialmodell „Orthotrop | Linear elastisch (Volumenkörper)“, während für den plastischen Bereich das Fließen nach Tsai-Wu gilt. Bild 10 zeigt die Fließbedingungen sowohl für Flächen (2D) als auch Volumenkörper (3D).
Wenn der Wert von fy(σ) gemäß Tsai-Wu-Gleichung, ebener Spannungszustand, kleiner als 1 ist, sind die Spannungen im elastischen Bereich. Der plastische Bereich wird erreicht, sobald fy(σ) = 1 ist. Werte über 1 sind nicht zulässig. Das Modellverhalten ist ideal plastisch, das heißt, es erfolgt keine Aussteifung.
Zusammenfassung
Das Add-On Nichtlineares Materialverhalten ermöglicht die Berücksichtigung von Materialnichtlinearitäten in RFEM 6. Wenn Sie dieses Add-On in den Basisangaben des Modells aktivieren, erweitert sich die Liste der Materialmodelle und Sie können ganz einfach das gewünschte nichtlineare Materialmodell auswählen.
Beim Arbeiten mit nichtlinearen Materialmodellen führt das Programm immer eine iterative Berechnung durch. Abhängig vom gewählten Modell wird eine andere Beziehung zwischen den Spannungen und Dehnungen definiert. Die Steifigkeit der finiten Elemente wird im Laufe der Iterationen kontinuierlich angepasst, bis die Spannungs-Dehnungs-Beziehung erfüllt ist.
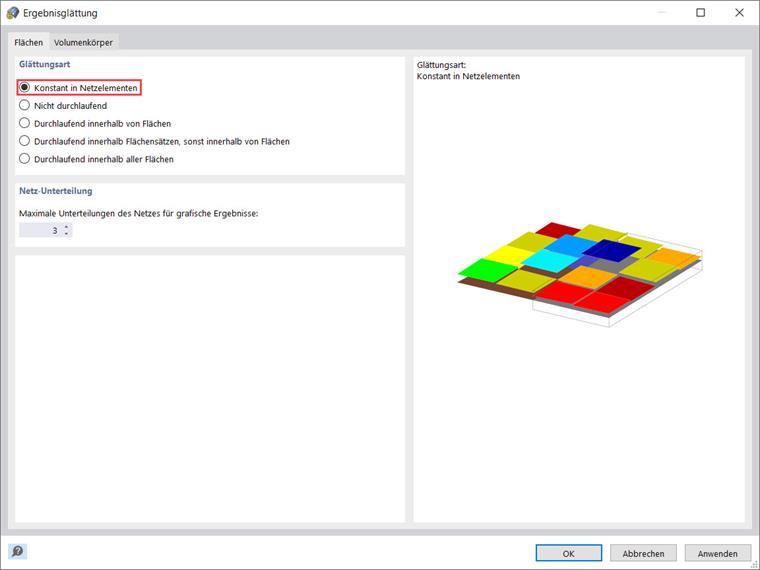
Die Anpassung erfolgt immer für ein ganzes Flächen- oder Volumenelement. Daher wird empfohlen, bei der Auswertung von Spannungen immer den Glättungstyp "Konstant in Netzelementen" zu verwenden, wie in Bild 11 gezeigt.