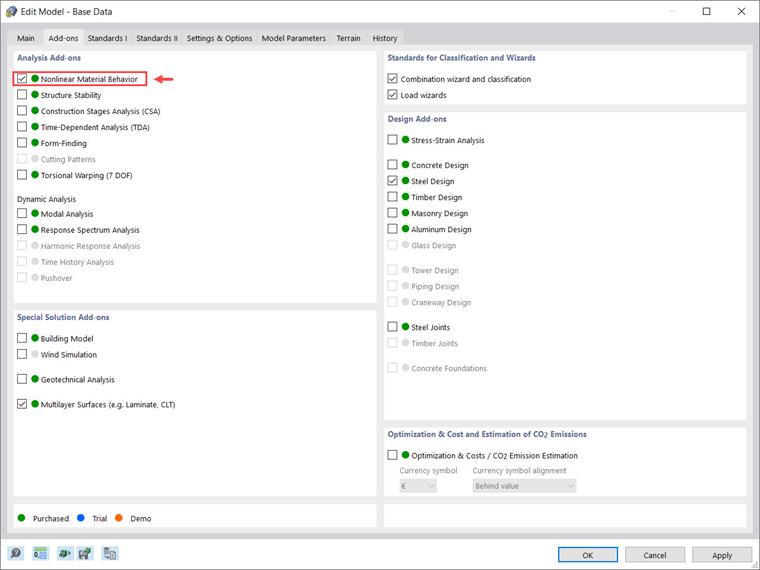
Dodatek do analizy nieliniowego zachowania materiału pozwala na uwzględnienie nieliniowości materiałowych w RFEM 6. Możesz aktywować ten dodatek w Danych Podstawowych modelu, jak pokazano na Obrazie 1.
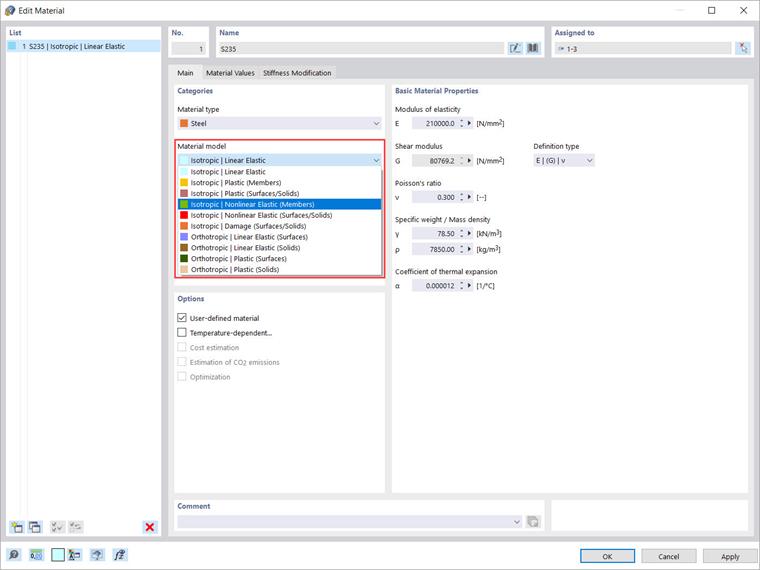
Po aktywowaniu dodatku do analizy nieliniowego zachowania materiału, oprócz modeli materiałowych „Izotropowy | Liniowo sprężysty” i „Ortotropowy | Liniowo sprężysty” dostępne są do wyboru dalsze opcje w liście (Obraz 2). Możesz zatem wybierać spośród następujących modeli materiałowych:
- Izotropowy | Plastyczny (Pręty)
- Izotropowy | Plastyczny (Powierzchnie/Bryły)
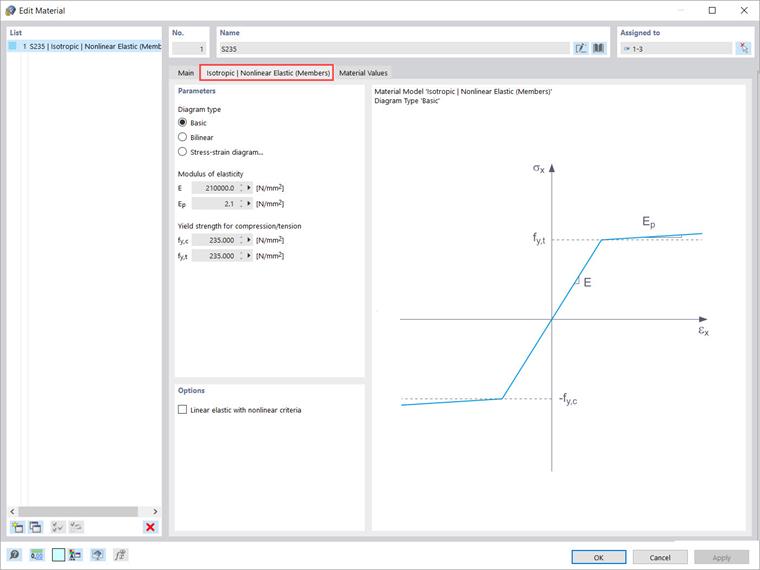
- Izotropowy | Nieliniowo sprężysty (Pręty)
- Izotropowy | Nieliniowo sprężysty (Powierzchnie/Bryły)
- Izotropowy | Uszkodzenie (Powierzchnie/Bryły)
- Ortotropowy | Plastyczny (Powierzchnie)
- Ortotropowy | Plastyczny (Bryły)
Izotropowy | Plastyczny (Pręty) Model Materiałowy
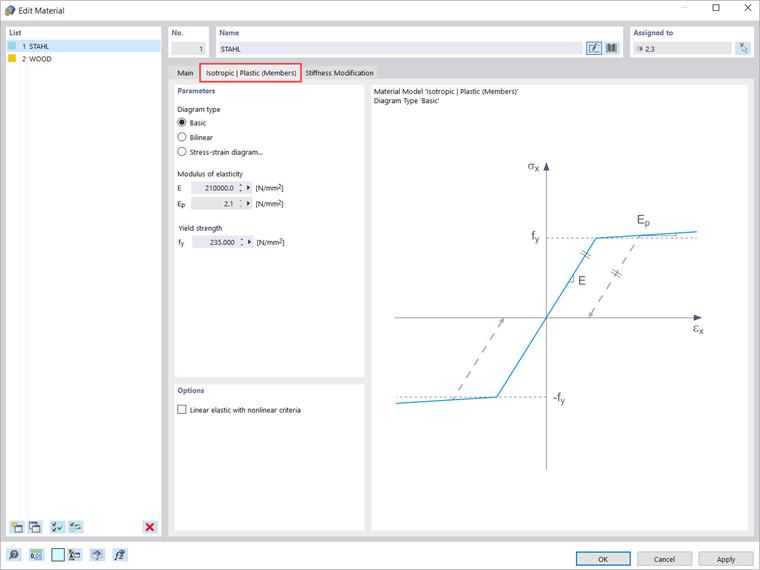
Jeśli wybierzesz jedną z powyższych pozycji w rozwijanym menu "Model materiałowy", pojawi się nowa zakładka do wprowadzania parametrów materiałowych. Dlatego wybierając model materiałowy "Izotropowy | Plastyczny (Pręty)”, pojawi się powiązana zakładka jak pokazano na Obrazie 3.
Najpierw masz możliwość wyboru następujących opcji dla typu wykresu:
- Podstawowy
- Dwuliniowy
- Wykres naprężenie-odkształcenie
Jeśli wybierzesz pierwszą opcję (czyli „Podstawowy”), program używa wartości z bazy danych materiałów dla modułu sprężystości E i granicy plastyczności fy. Należy zauważyć, że jest to również model materiałowy dwuliniowy, gdzie gałąź wykresu nie jest dokładnie pozioma ze względów numerycznych i posiada niewielkie nachylenie Ep. Natomiast jeśli wykres jest zdefiniowany dwuliniowo (czyli opcja „Dwuliniowy”), program pozwala na samodzielne wprowadzenie wartości Ep.
Trzecia dostępna opcja (czyli „Wykres naprężenie-odkształcenie”) pozwala na zdefiniowanie bardziej złożonych zależności między naprężeniem a odkształceniem. Należy zauważyć, że w tym modelu materiałowym wykres naprężenie-odkształcenie odnosi się do naprężeń wzdłużnych σx. Różne punkty plastyczności dla naprężeń ściskających i rozciągających nie mogą być uwzględnione tą opcją.
Izotropowy | Plastyczny (Powierzchnie/Bryły) Model Materiałowy
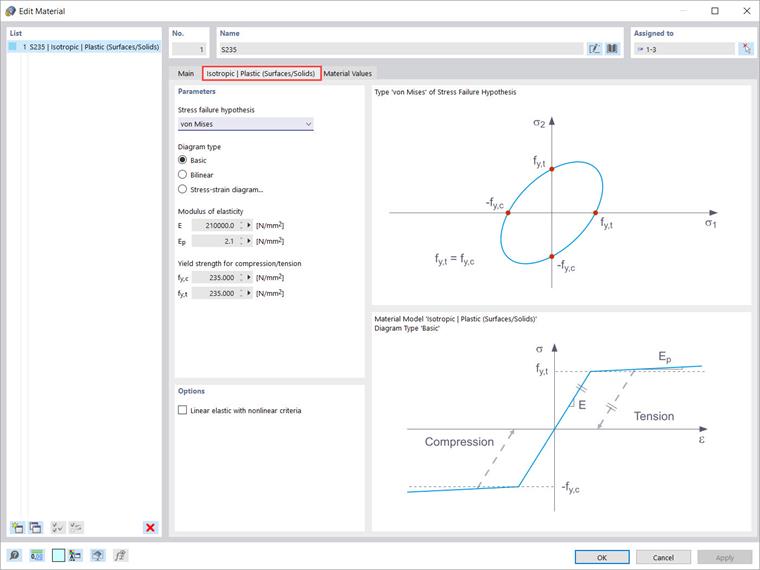
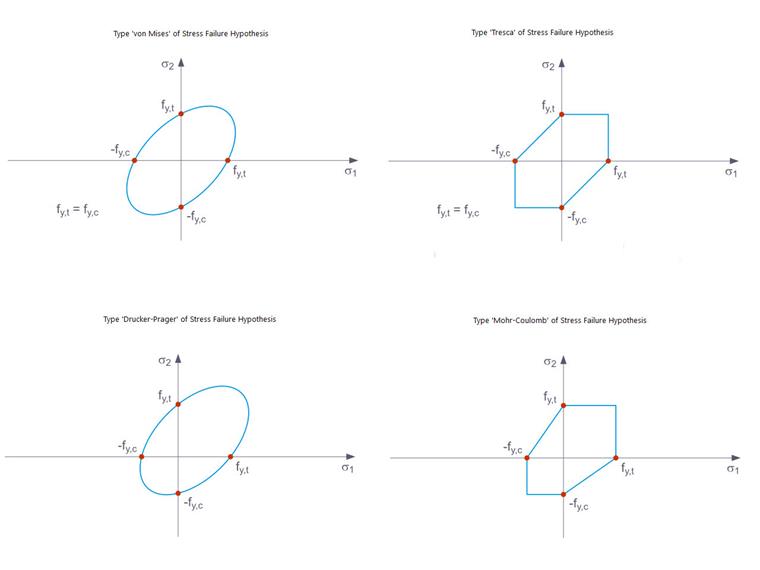
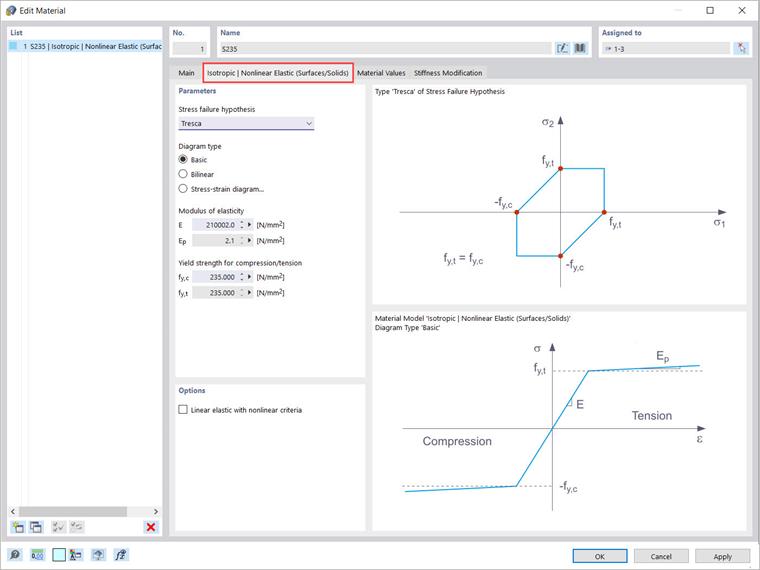
Izotropowy plastyczny model materiałowy jest również dostępny dla powierzchni i brył. W taki sam sposób jak dla modelu „Izotropowy | Plastyczny (Pręty)”, odpowiednia zakładka pojawia się po wybraniu pozycji „Izotropowy | Plastyczny (Powierzchnie/Bryły)” w rozwijanej liście. Oprócz opcji definiowania typu wykresu (takie same jak dla „Izotropowy | Plastyczny (Pręty)”), należy wybrać „Hipotezę zniszczenia naprężeniowego” (Obraz 4).
W rozwijanym menu dostępne są do wyboru następujące hipotezy zniszczenia naprężeniowego:
- von Mises
- Tresca
- Drucker-Prager
- Mohr-Coulomb
Kryterium plastyczności według von Misesa to cylindryczny kształt z osią hydrostatyczną w przestrzeni naprężeń głównych. Wszystkie stany naprężeniowe w obrębie tej przestrzeni są całkowicie sprężyste. Stany naprężeniowe poza tą przestrzenią nie są dozwolone. Zasada plastyczności Tresca powoduje występowanie plastyczności z powodu maksymalnego naprężenia stycznego.
Jako rozszerzenie tych kryteriów plastyczności, istnieją zasady plastyczności według Drucker-Pragera i Mohr-Coulomba, w których plastyczność występuje, gdy maksymalne naprężenie styczne jest lokalnie przekroczone. Pierwsza z nich to obszar o gładkiej granicy w przestrzeni naprężeń głównych, podczas gdy druga to obszar o niegładkiej granicy (Obraz 5).
Izotropowy | Nieliniowo Sprężysty (Pręty) Model Materiałowy
Zakładka do ustawienia parametrów modelu „Izotropowy | Nieliniowo Sprężysty (Pręty)” jest bardzo podobna do modelu materiałowego „Izotropowy | Plastyczny (Pręty)” (Obraz 6). W rzeczywistości te modele odpowiadają sobie. Różnica między nimi dotyczy ogólnego rozróżnienia między modelami materiałów nieliniowo sprężystych z jednej strony, a plastycznymi z drugiej strony.
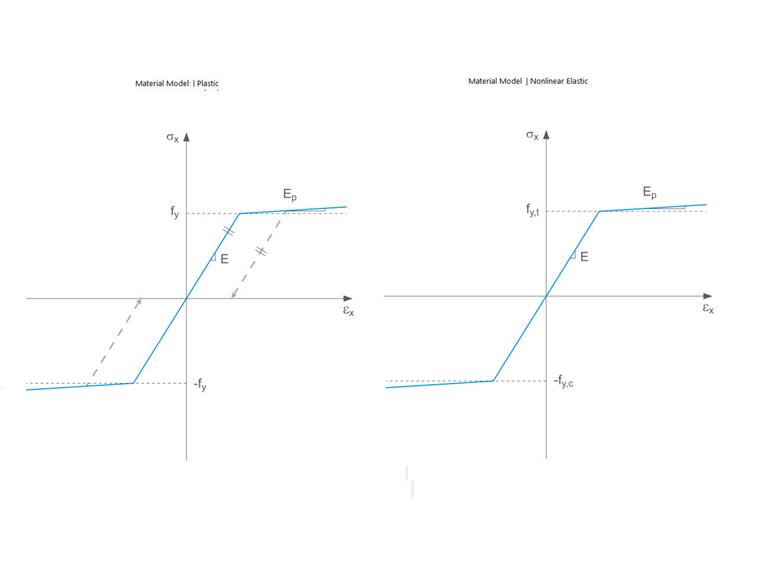
Jeśli element konstrukcyjny o nieliniowo sprężystym materiale zostanie rzeczywiście odciążony, odkształcenie wraca tą samą ścieżką i nie ma już odkształcenia, gdy element jest całkowicie odciążony. W przypadku materiałów plastycznych, z drugiej strony, odkształcenie pozostaje nawet po całkowitym odciążeniu elementu. Jest to przedstawione graficznie na Obrazie 7.
Izotropowy | Nieliniowo Sprężysty (Powierzchnie/Bryły) Model Materiałowy
Ta sama dyskusja dotyczy zależności między modelami „Izotropowy | Plastyczny (Powierzchnie/Bryły)” a „Izotropowy | Nieliniowo Sprężysty (Powierzchnie/Bryły)”. Właściwości modelu powinny być zdefiniowane w ten sam sposób (Obraz 8), z tą różnicą, że po usunięciu obciążenia nie pozostają plastyczne odkształcenia.
Izotropowy | Uszkodzenie (Powierzchnie/Bryły) Model Materiałowy
Wcześniej wspomniane zasady plastyczności w artykule są ograniczone do powierzchni plastyczności w przestrzeni naprężeń głównych, a ich zasady plastyczności mogą dotyczyć tylko czysto sprężysto-plastycznego zachowania materiału. Jednak wiele materiałów nie wykazuje czysto symetrycznego nieliniowego zachowania. Aby symulować zachowanie materiałów, które są narażone na proces uszkodzenia spowodowany pęknięciami, wymagany jest bardziej odpowiedni model materiałowy. Jednym z takich materiałów jest beton, który ma znacznie wyższą wytrzymałość na ściskanie niż na rozciąganie.
Pęknięcia, które występują w strefie rozciągania materiału, zmniejszają sztywność systemu. W przypadku betonu zbrojonego lub betonu zbrojonego włóknami, zbrojenie absorbuje naprężenia rozciągające.
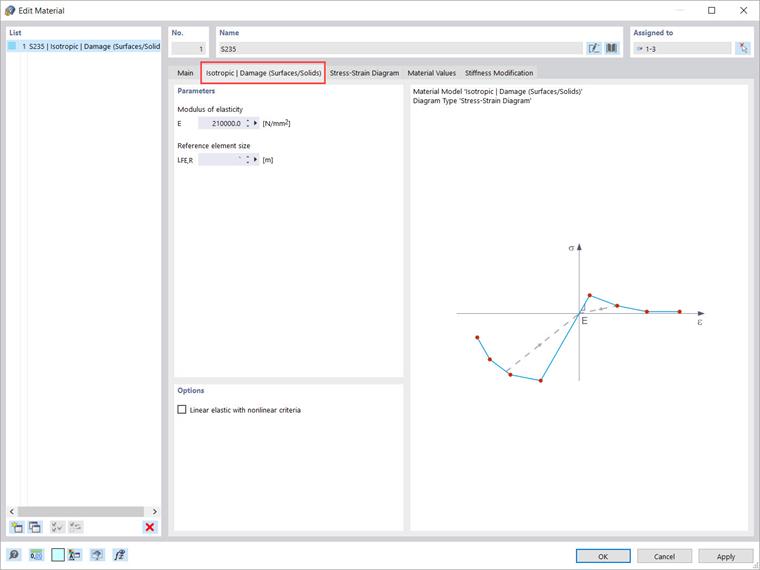
Aby symulować zachowanie takich materiałów (na przykład betonu zbrojonego włóknami stalowymi), RFEM 6 oferuje model materiałowy „Izotropowy | Uszkodzenie (Powierzchnie/Bryły)”. Jeśli wybierzesz ten model materiałowy, dostępna jest zakładka pokazana na Obrazie 9, aby zdefiniować parametry modelu.
W przeciwieństwie do innych modeli materiałowych, wykres naprężenie-odkształcenie dla tego modelu materiałowego nie jest antymetryczny względem początku. "Rozmiar elementu referencyjnego" kontroluje, jak odkształcenie w obszarze pęknięcia jest skalowane do długości elementu. Z domyślną wartością zero, żadne skalowanie nie jest wykonywane. W rezultacie, zachowanie materiału betonu zbrojonego włóknami stalowymi jest modelowane realistycznie.
Ortotropowy | Plastyczny (Powierzchnie, Bryły) | Model Materiałowy Tsai-Wu
Za pomocą ortotropowego modelu materiałowego plastycznego dla powierzchni i brył w RFEM 6, powierzchnie i bryły o plastycznych właściwościach materiałowych mogą być obliczane i oceniane zgodnie z kryterium zniszczenia Tsai-Wu. Ten model materiałowy łączy właściwości plastyczne i ortotropowe, co pozwala na specjalne modelowanie materiałów o anizotropowych właściwościach. Ten model materiałowy może być zatem używany do reprezentowania zachowania tworzyw sztucznych wzmacnianych włóknami lub paneli drewnopochodnych.
W tym modelu materiałowym zakres sprężysty odpowiada modelowi materiałowemu „Ortotropowy | Liniowo Sprężysty (Bryły)”, podczas gdy dla domeny plastycznej, plastyczność jest stosowana zgodnie z Tsai-Wu. Obraz 10 pokazuje warunki plastyczności dla obu powierzchni (2D) i brył (3D).
Jeśli wartość fy(σ) według równania Tsai-Wu, stan naprężeń płaskich, jest mniejsza niż 1, naprężenia są w zakresie sprężystym. Domena plastyczna jest osiągana, gdy tylko fy(σ) = 1. Wartości powyżej 1 nie są dozwolone. Zachowanie modelu jest idealnie plastyczne; to znaczy, nie występuje usztywnienie.
Podsumowanie
Dodatek do analizy nieliniowego zachowania materiału umożliwia uwzględnienie nieliniowości materiałowych w RFEM 6. Jeśli aktywujesz ten dodatek w Danych Podstawowych modelu, lista modeli materiałowych rozszerza się i możesz łatwo wybrać interesujący Cię model materiałowy nieliniowy.
Podczas pracy z modelami materiałów nieliniowych, program zawsze wykonuje obliczenia iteracyjne. W zależności od wybranego modelu definiuje inne zależności między naprężeniami a odkształceniami. Sztywność elementów skończonych jest ciągle dostosowywana w trakcie iteracji do momentu, gdy związek naprężenie-odkształcenie zostanie spełniony.
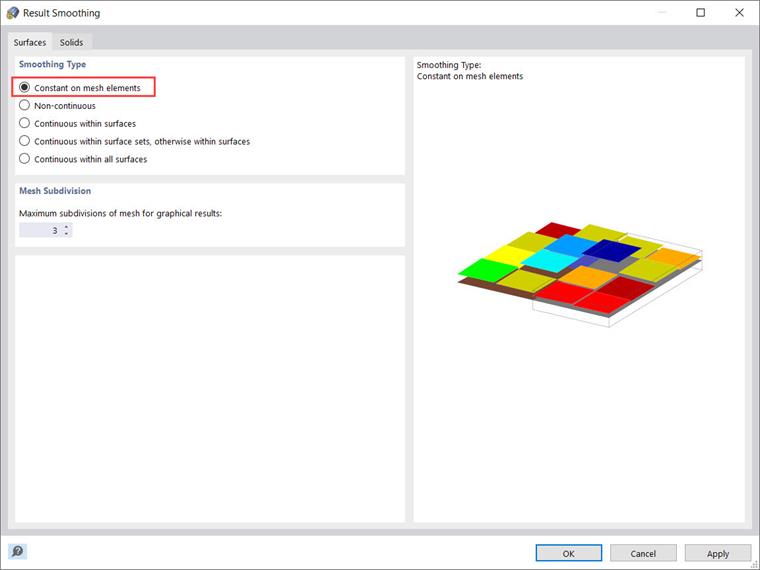
Dostosowanie jest zawsze realizowane dla całej powierzchni lub elementu bryłowego. Dlatego zaleca się zawsze stosowanie typu wygładzania "Stały na elementach siatki" podczas oceny naprężeń, jak pokazano na Obrazie 11.