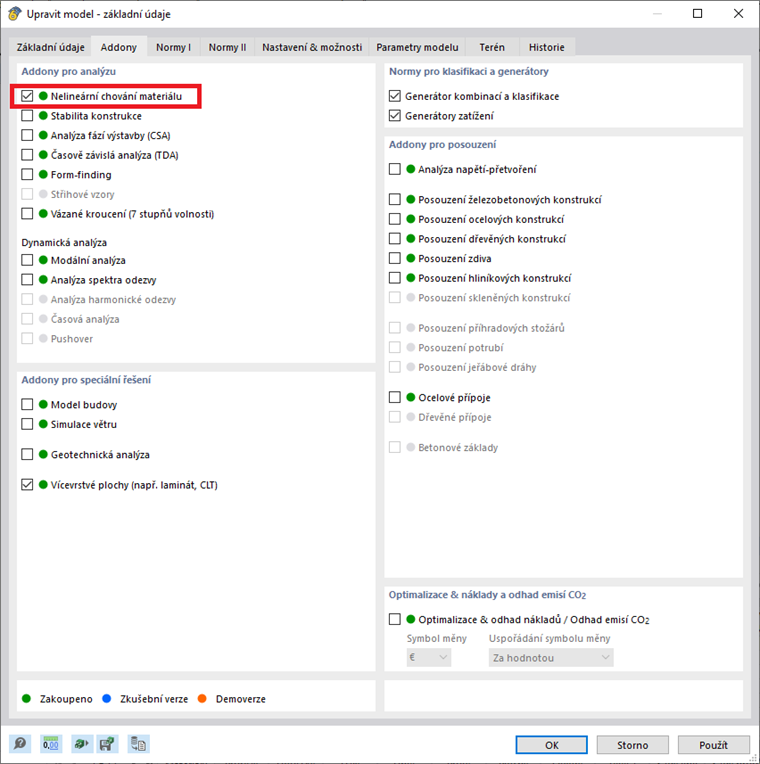
Doplněk "Nelineární materiálové chování" umožňuje zohlednit materiálové nelinearity v programu RFEM 6. Tento doplněk můžete aktivovat v základních datech modelu, jak je ukázáno na obrázku 1.
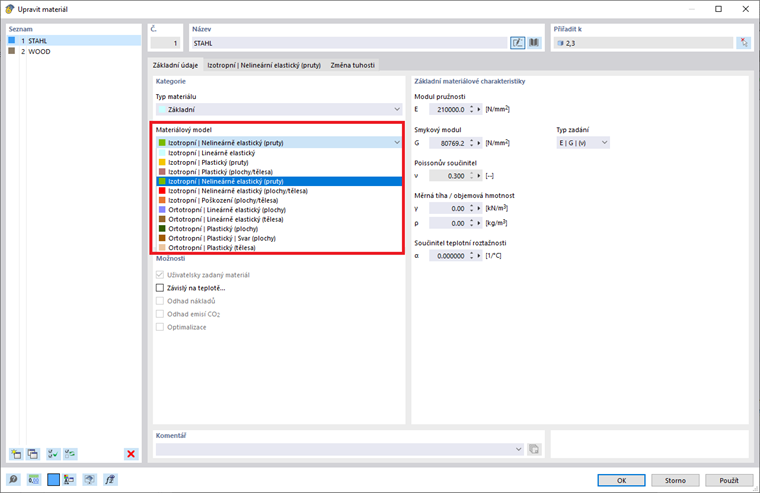
Jakmile je doplněk pro analýzu Nelineární materiálové chování aktivován, kromě materiálových modelů “Izotropní | Lineárně elastický” a “Ortropní | Lineárně elastický” jsou v seznamu k dispozici další možnosti výběru (obrázek 2). Můžete si tedy vybrat z následujících materiálových modelů:
- Izotropní | Plastický (Pruty)
- Izotropní | Plastický (Pláty/Tuhé tělesa)
- Izotropní | Nelineárně elastický (Pruty)
- Izotropní | Nelineárně elastický (Pláty/Tuhé tělesa)
- Izotropní | Poškození (Pláty/Tuhé tělesa)
- Ortropní | Plastický (Pláty)
- Ortropní | Plastický (Tuhé tělesa)
Materiálový model Izotropní | Plastický (Pruty)
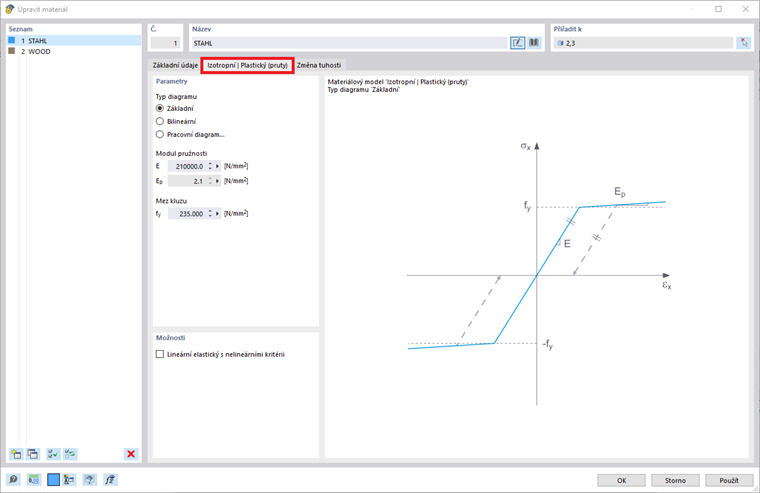
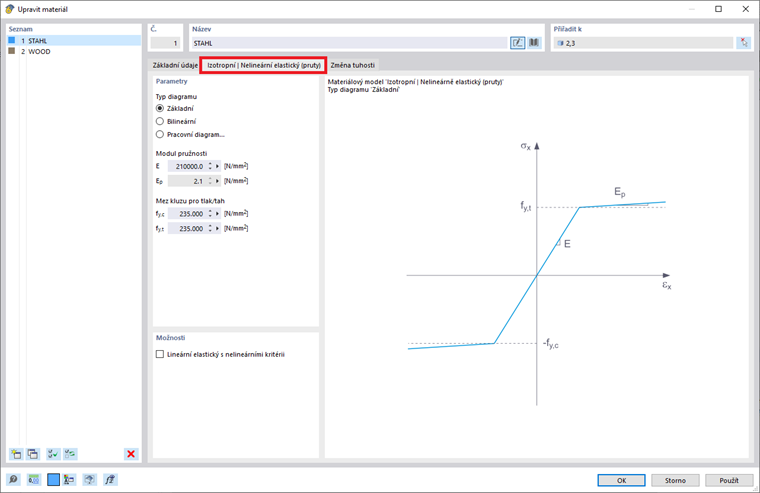
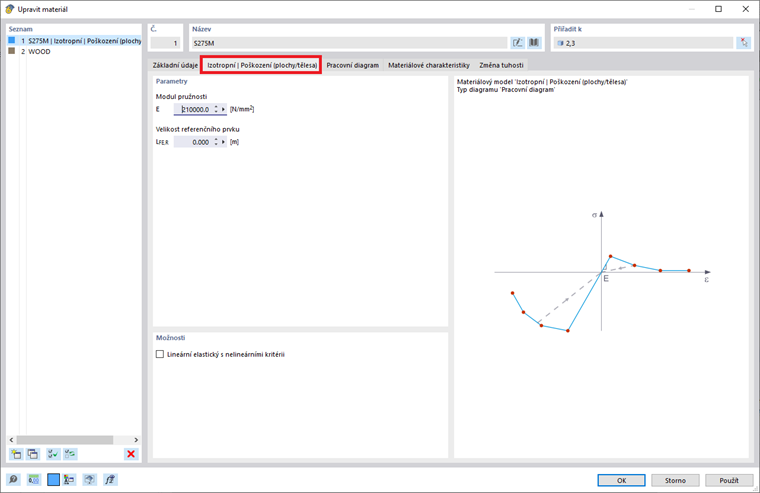
Pokud vyberete jednu z výše uvedených položek v rozbalovacím seznamu "Materiálový model", je k dispozici nová karta pro zadání materiálových parametrů. Proto při výběru materiálového modelu "Izotropní | Plastický (Pruty)” se objeví související karta, jak je znázorněno na obrázku 3.
Nejprve máte možnost vybrat následující možnosti pro typ diagramu:
- Základní
- Bilineární
- Diagram napětí-deformace
Pokud zvolíte první možnost (tedy “Základní”), program použije hodnoty z materiálové databáze pro modul pružnosti E a mez kluzu fy. Upozorňujeme, že se jedná také o bilineární materiálový model, kde větev grafu není přesně horizontální z numerických důvodů a má malý sklon Ep. Naopak, pokud je diagram definován bilineárně (tedy možnost “Bilineární”), program vám umožňuje zadat hodnotu Ep sami.
Třetí dostupná možnost (tedy “Diagram napětí-deformace”) vám umožňuje definovat složitější vztahy mezi napětím a deformací. Vezměte prosím na vědomí, že v tomto materiálovém modelu se diagram napětí-deformace týká podélného napětí σx. Různé body kluzu pro tah a tlak nelze touto volbou zohlednit.
Materiálový model Izotropní | Plastický (Pláty/Tuhé tělesa)
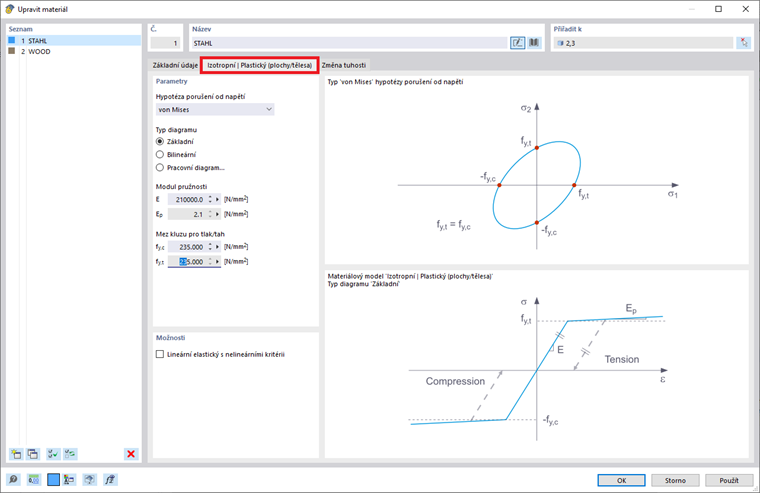
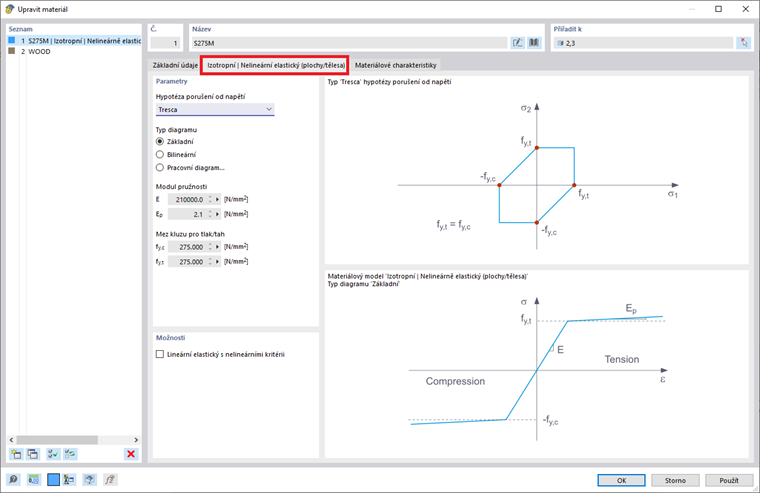
Izotropní plastický materiálový model je také k dispozici pro pláty a tuhý tělesa. Stejně jako u modelu “Izotropní | Plastický (Pruty)” se objeví související karta při výběru položky “Izotropní | Plastický (Pláty/Tuhé tělesa)” v rozbalovacím seznamu. Kromě možností pro definování typu diagramu (stejných jako pro “Izotropní | Plastický (Pruty)”) musí být vybrána “Hypotéza porušení napětí” (obrázek 4).
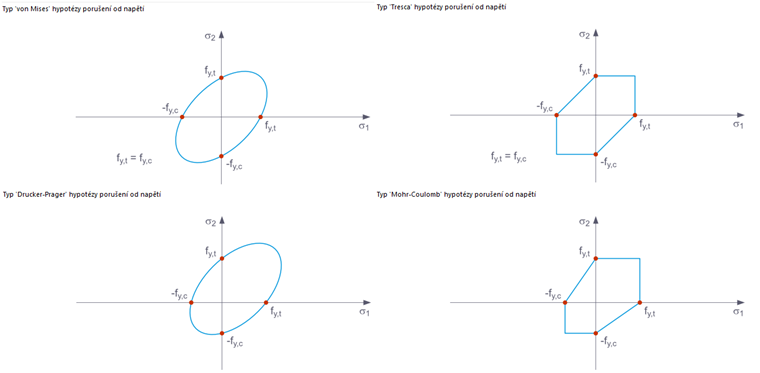
V rozbalovacím menu jsou k výběru k dispozici následující hypotézy porušení napětí:
- von Mises
- Tresca
- Drucker-Prager
- Mohr-Coulomb
Kriterium kluzu podle von Mise je válcová plocha s hydrostatickou osou v prostoru hlavních napětí. Všechny stavy napětí v tomto prostoru jsou zcela elastické. Stavy napětí mimo tento prostor nejsou povoleny. S Trescovým kriteriem kluzu nastává plastické klouzání v důsledku maximálního smykového napětí.
Jako rozšíření těchto kritérií kluzu jsou pravidla kluzu podle Druckera-Pragera a Mohr-Coulomba, kde nastává plastické klouzání, pokud je lokálně překročeno maximální smykové napětí. V prvním případě je v prostoru hlavního napětí plocha s hladkou hranicí, zatímco v druhém případě je to plocha s nehladkou hranicí (obrázek 5).
Materiálový model Izotropní | Nelineárně elastický (Pruty)
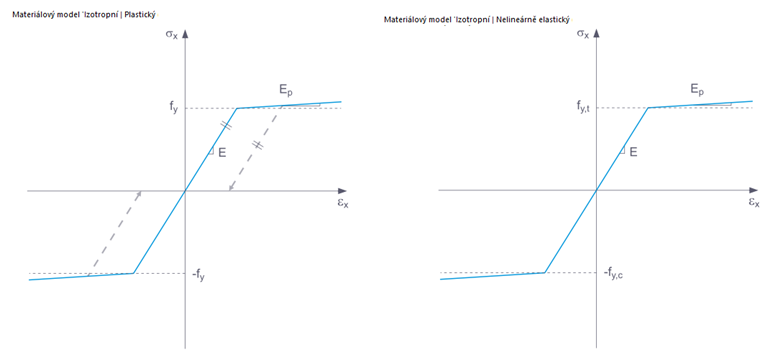
Karta pro nastavení parametrů modelu “Izotropní | Nelineárně elastický (Pruty)” je velmi podobná té u materiálového modelu “Izotropní | Plastický (Pruty)” (obrázek 6). Ve skutečnosti tyto modely odpovídají navzájem. Rozdíl mezi nimi se týká obecného rozlišení mezi nelineárními elastickými materiály na jedné straně a plastickými na druhé straně.
Pokud je konstrukční komponenta s nelineárním elastickým materiálem skutečně znovu uvolněna, deformace se vrátí po stejné cestě a při úplném odlehčení komponenty již nedochází k žádné deformaci. Naopak, v případě plastických materiálů deformace zůstává i po úplném odlehčení. To je graficky znázorněno na obrázku 7.
Materiálový model Izotropní | Nelineárně elastický (Pláty/Tuhé tělesa)
Stejná diskuse platí pro souvztažnost mezi materiálovými modely “Izotropní | Plastický (Pláty/Tuhé tělesa)” a “Izotropní | Nelineárně elastický (Pláty/Tuhé tělesa)”. Vlastnosti modelu by měly být definovány stejným způsobem (obrázek 8), s tím rozdílem, že po odstranění zátěže nezůstává žádná plastická deformace.
Materiálový model Izotropní | Poškození (Pláty/Tuhé tělesa)
Výše uvedené zákony kluzu jsou omezeny na povrch kluzu v prostoru hlavních napětí a jejich pravidla kluzu mohou pouze platit pro čistě elasticko-plastické chování materiálu. Nicméně mnoho materiálů nevykazuje čistě symetrické nelineární chování. Abychom simulovali chování materiálů, které podléhají procesu poškození způsobeného trhlinami, je vyžadován vhodnější materiálový model. Jedním takovým materiálem je beton, který má výrazně vyšší tlakovou pevnost než tahovou pevnost.
Trhliny, které se v materiálu v oblasti tahu objevují, snižují tuhost systému. V případě železobetonu nebo železovláknobetonu vyztužení absorbuje tahová napětí.
Aby bylo možné simulovat chování takových materiálů (například ocelovláknobetonu), nabízí RFEM 6 materiálový model “Izotropní | Poškození (Pláty/Tuhé tělesa)”. Pokud vyberete tento materiálový model, je k dispozici karta ukázaná na obrázku 9 pro definování parametrů modelu.
Na rozdíl od jiných materiálových modelů není diagram napětí-deformace pro tento materiálový model antisymetrický k původu. "Referenční velikost prvku" řídí, jak je deformace v oblasti trhliny škálována vůči délce prvku. S výchozí hodnotou nula se neprovádí žádné škálování. Výsledkem je, že chování materiálu ocelovláknobetonu je modelováno realisticky.
Materiálový model Ortropní | Plastický (Pláty, Tuhé tělesa) | Tsai-Wu
S ortropním plastickým materiálovým modelem pro pláty a tuhý tělesa v RFEM 6 lze pláty a tuhý tělesa s plastickými vlastnostmi počítat a vyhodnocovat podle kritéria porušení Tsai-Wu. Tento materiálový model kombinuje plastické a ortropní vlastnosti, což umožňuje speciální modelování materiálů s anizotropními vlastnostmi. Tento materiálový model lze tedy použít k reprezentaci chování vláknem vyztužených plastů nebo desek na bázi dřeva.
V tomto materiálovém modelu odpovídá elastická oblast materiálovému modelu “Ortropní | Lineárně elastický (Tuhé tělesa)”, zatímco pro plastickou oblast platí klouzání podle Tsai-Wu. Obrázek 10 ukazuje podmínky kluzu pro jak pláty (2D), tak tuhý tělesa (3D).
Pokud je hodnota fy(σ) podle rovnice Tsai-Wu, stav roviny napjatosti, menší než 1, jsou napětí v elastické oblasti. Plastická oblast je dosažena jakmile fy(σ) = 1. Hodnoty nad 1 nejsou povoleny. Chování modelu je ideálně plastické, tedy nedochází k zpevnění.
Shrnutí
Doplněk "Nelineární materiálové chování" umožňuje zohlednění materiálových nelinearit v RFEM 6. Pokud tento doplněk v základních datech modelu aktivujete, seznam materiálových modelů se rozšíří a můžete snadno vybrat nelineární materiálový model podle vašeho zájmu.
Při práci s nelineárními materiálovými modely provádí program vždy iterativní výpočet. V závislosti na vybraném modelu definuje odlišný vztah mezi napětími a deformacemi. Tuhost konečných prvků je průběžně upravována během iterací, dokud není splněn vztah napětí-deformace.
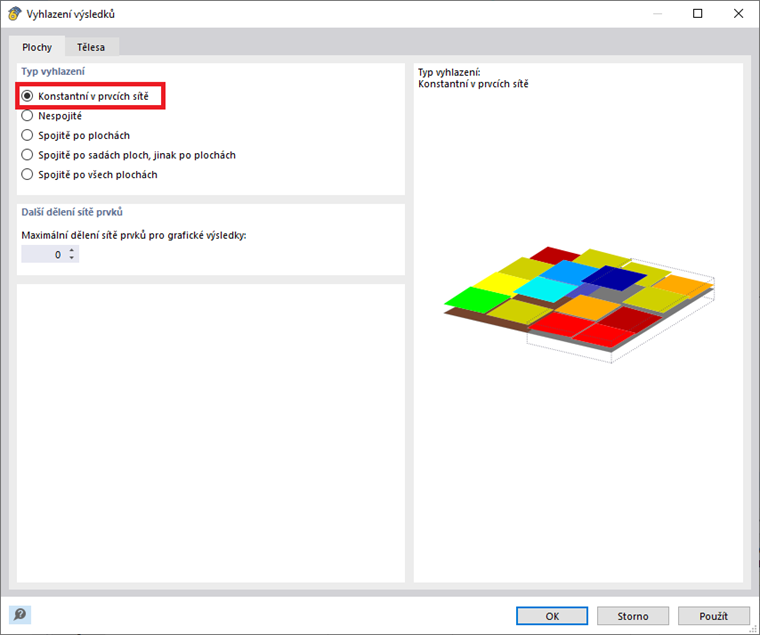
Úprava je vždy provedena pro celý povrch nebo tuhý prvek. Proto se doporučuje vždy použít typ vyhlazení "Konstantní na síťových prvcích" při vyhodnocení napětí, jak je ukázáno na obrázku 11.