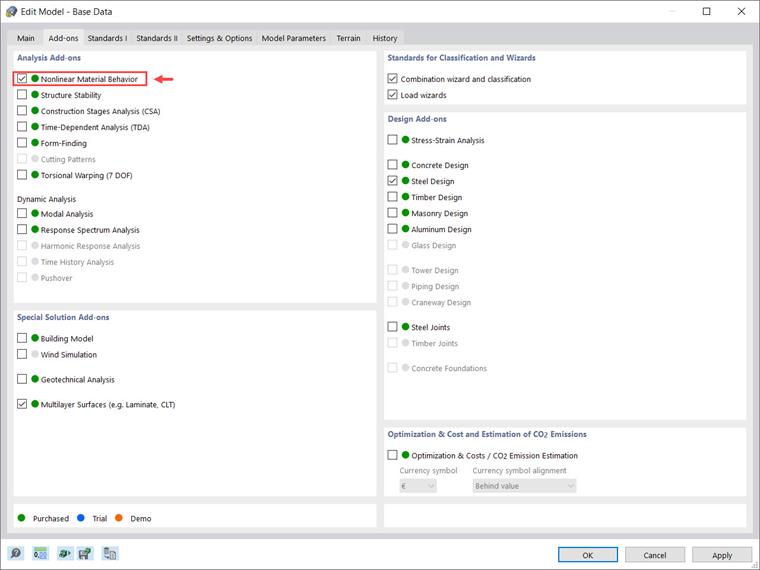
O módulo Comportamento de Materiais Não Linear permite considerar as não-linearidades dos materiais no RFEM 6. O utilizador pode ativar este módulo nos Dados gerais do modelo conforme apresentado na Imagem 1.
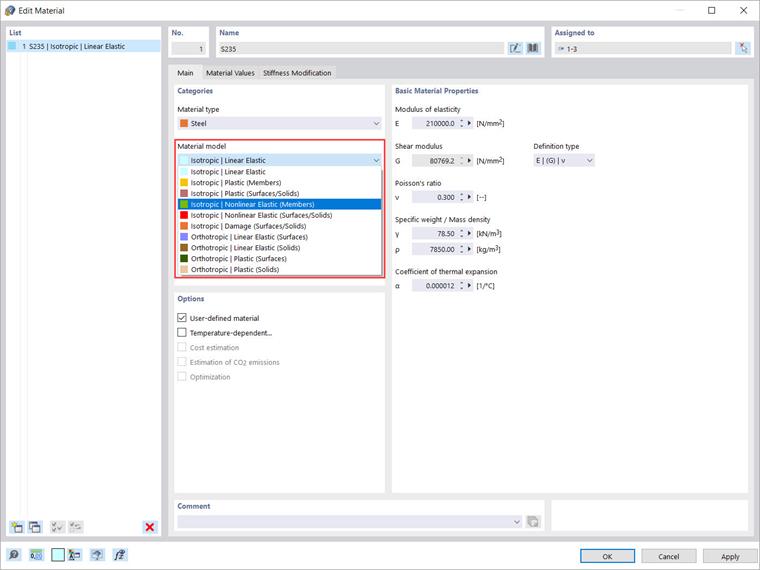
Uma vez que a análise do módulo Comportamento de Materiais Não Linear é ativada, além dos modelos de material “Isotrópico | linear elástico” e “Ortótropo | linear elástico”, outras opções estão disponíveis para seleção na lista (Imagem 2). Portanto, pode escolher entre os seguintes modelos de materiais:
- Isotrópico | Plástico (Barras)
- Isotrópico | Plástico (Superfícies/Sólidos)
- Isotrópico | Não linear elástico(Barras)
- Isotrópico | Não linear elástico (Superfícies/Sólidos)
- Isotrópico | Dano (Superfícies/Sólidos)
- Ortótropo | Plástico (Superfícies)
- Ortótropo | Plástico (Sólidos)
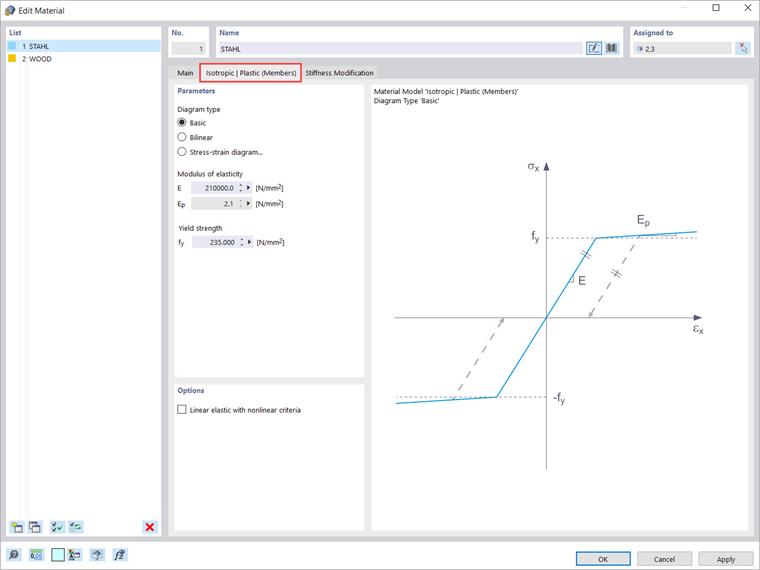
Modelo de material isotrópico | plástico (Barras)
Se selecionar uma das opções acima na lista suspensa "Modelo de material", um novo separador estará disponível para inserir os parâmetros do material. Assim, ao selecionar o modelo de material "Isotrópico | Plástico (Barras)", aparecerá um separador relacionado conforme mostrado na Imagem 3.
Primeiro, tem a possibilidade de selecionar as seguintes opções para o tipo de diagrama:
- Básico
- Bilinear
- Diagrama tensão-deformação
Ao selecionar a primeira opção (ou seja, “Básico”), o programa utiliza valores da base de dados de materiais para o módulo de elasticidade E e a tensão de cedência fy. Note que este também é um modelo de material bilinear, onde o ramo do gráfico não é exatamente horizontal por razões numéricas e tem uma pequena inclinação Ep. Em contraste, se o diagrama for definido de forma bilinear (ou seja, a opção “Bilinear”), o programa permite que você insira o valor de Ep por si mesmo.
A terceira opção disponível (ou seja, “Diagrama tensão-deformação”) permite definir relações mais complexas entre a tensão e a deformação. Observe que, neste modelo de material, o diagrama tensão-deformação refere-se à tensão longitudinal σx. Para esta opção não ser considerados diferentes pontos de cedência para a tração e a compressão.
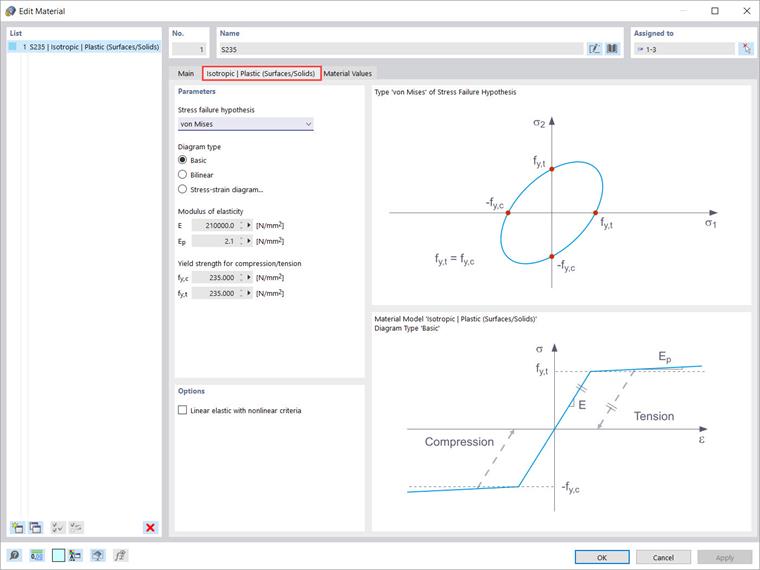
Modelo de material isotrópico | plástico (superfícies/sólidos)
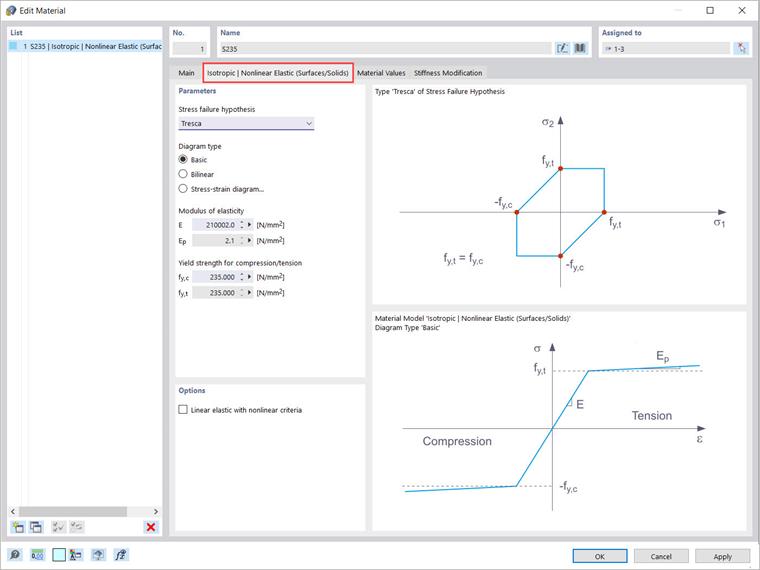
O modelo de material plástico isotrópico também está disponível para superfícies e sólidos. Da mesma forma que para o modelo “Isotrópico | plástico (barras)”, aparece um separador relativo ao selecionar a entrada “Isotrópico | plástico (superfícies/sólidos)” na lista suspensa. Além das opções para definir o tipo de diagrama (as mesmas do “Isotrópico | plástico (barras)”), a “Hipótese de rotura por tensão” deve ser selecionada (Imagem 4).
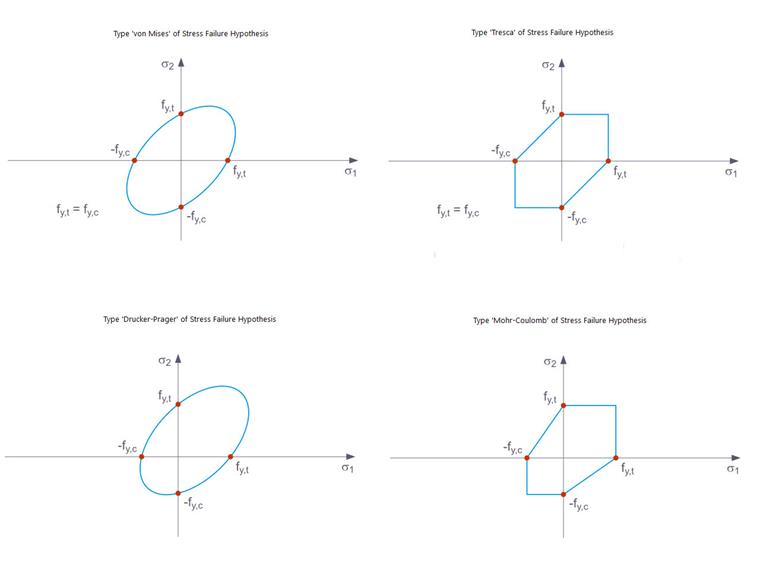
As seguintes hipóteses de rotura por tensão estão disponíveis para seleção no menu suspenso:
- von Mises
- Tresca
- Drucker-Prager
- Mohr-Coulomb
O critério de cedência de von Mises é um cilindro circular com um eixo hidrostático no espaço de tensões principais. Todos os estados de tensão dentro deste espaço são completamente elásticos. Estados de tensão fora deste espaço não são permitidos. Com a regra de cedência de Tresca, a cedência plástica ocorre devido à tensão de corte máxima.
Como uma extensão desses critérios de escoamento, existem as regras de cedência de acordo com Drucker-Prager e Mohr-Coulomb, nas quais a cedência plástica ocorre quando a tensão de corte máxima é excedida localmente. Na primeira, há uma área de superfície com uma borda suave no espaço de tensões principais, enquanto na última é uma área de superfície com uma borda não suave (Imagem 5).
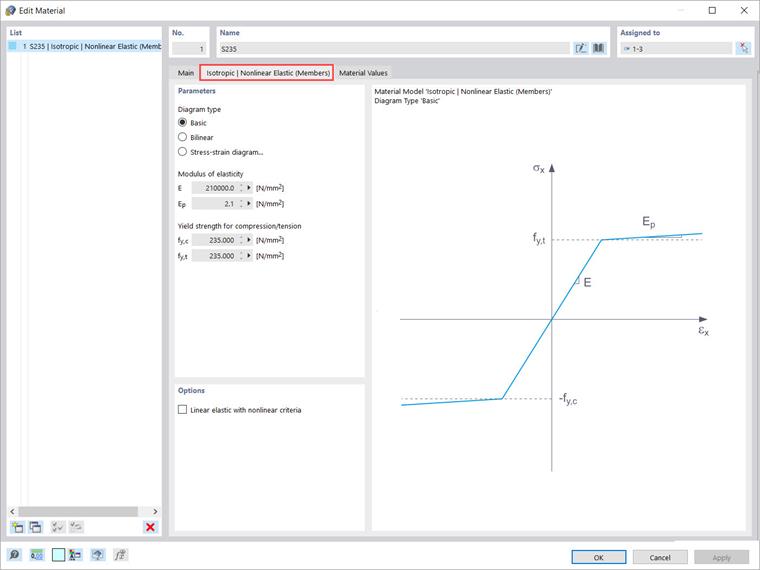
Modelo de material isotrópico | não linear elástico (Barras)
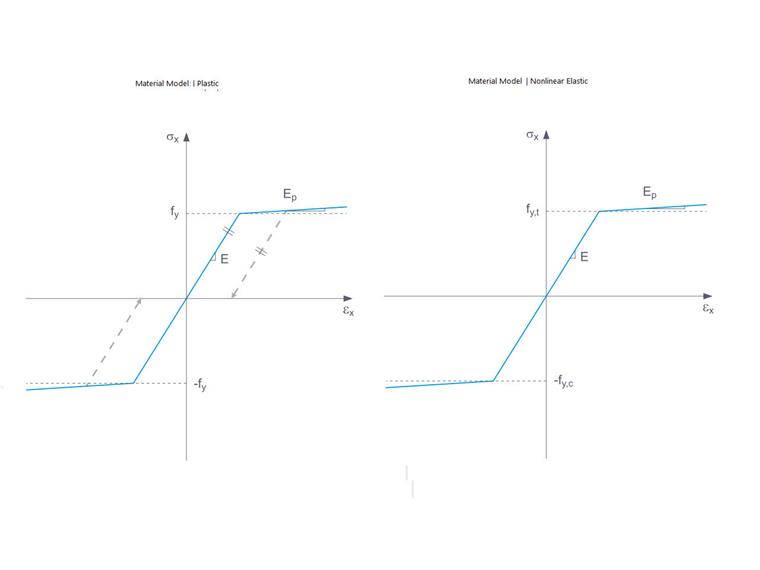
O separador para definir os parâmetros do modelo “Isotrópico | não linear elástico (Barras)” é muito semelhante à do modelo de material “Isotrópico | Plástico (Barras)” (Imagem 6). De fato, esses modelos correspondem entre si. A diferença entre eles está relacionada com a distinção geral entre os modelos de materiais elásticos não lineares por um lado, e os plásticos por outro.
Se um componente estrutural com um material não linear elástico for realmente libertado novamente, a deformação retorna pelo mesmo caminho e não há mais qualquer deformação quando o componente está completamente descarregado. No caso de materiais plásticos, por outro lado, a deformação permanece mesmo após a carga ter sido completamente removida. Isso é mostrado graficamente na Imagem 7.
Modelo de material isotrópico | não linear elástico (Superfícies/Sólidos)
A mesma discussão aplica-se à correspondência entre os modelos de material “Isotrópico | plástico (Superfícies/Sólidos)” e “Isotrópico | não linear elástico (Superfícies/Sólidos)”. As propriedades do modelo devem ser definidas da mesma forma (Imagem 8), com a diferença de que nenhuma deformação plástica permanece após a remoção da carga.
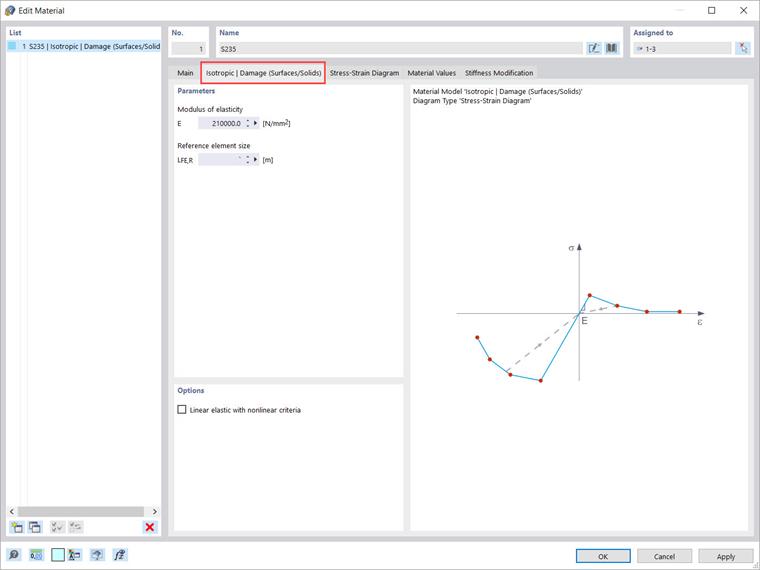
Modelo de material isotrópico | dano (Superfícies/Sólidos)
As leis de cedência mencionadas anteriormente no artigo são restritas à superfície de cedência no espaço de tensões principais, e suas regras de cedência só podem aplicar-se a um comportamento de material puramente elástico-plástico. No entanto, muitos materiais não apresentam um comportamento não linear puramente simétrico. Para simular o comportamento de materiais expostos a um processo de dano causado por fissuras, é necessário um modelo de material mais adequado. Um desses materiais é o betão, que apresenta uma resistência à compressão significativamente maior do que a resistência à tração.
As fissuras que ocorrem na área de tração do material reduzem a rigidez do sistema. No caso de betão armado ou betão reforçado com fibras, a armadura absorve as tensões de tração.
Para simular o comportamento de tais materiais (por exemplo, betão reforçado com fibras de aço), o RFEM 6 oferece o modelo de material “Isotrópico | dano (Superfícies/Sólidos)”. Se selecionar este modelo de material, o separador apresentado na Imagem 9 estará disponível para definir os parâmetros do modelo.
Ao contrário de outros modelos de materiais, o diagrama tensão-deformação para este modelo de material não é antissimétrico em relação à origem. O "Tamanho do elemento de referência" controla como a deformação na área de fissura é escalonada em relação ao comprimento do elemento. Com o valor definido por defeito é zero, nenhum é realizada qualquer relação de escala. Como resultado, o comportamento do material do betão reforçado com fibras de aço é modelado de forma realista.
Modelo de material ortótropo | plástico (Superfícies, Sólidos) | Tsai-Wu
Com o modelo de material plástico ortotrópico para superfícies e sólidos no RFEM 6, as superfícies e os sólidos com propriedades de material plástico podem ser calculados e avaliados de acordo com o critério de rotura de Tsai-Wu. Este modelo de material combina propriedades plásticas e ortotrópicas, o que permite modelar de maneira especial materiais com propriedades anisotrópicas. Este modelo de material pode, portanto, ser utilizado para representar o comportamento de plásticos reforçados com fibras ou painéis à base de madeira.
Neste modelo de material, o campo elástico corresponde ao modelo de material “Ortótropo | linear elástico (Sólidos)”, enquanto que para o domínio plástico, a cedência aplica-se de acordo com Tsai-Wu. A Imagem 10 mostra as condições de cedência para superfícies (2D) e sólidos (3D).
Se o valor de fy(σ) de acordo com a equação de Tsai-Wu, estado plano de tensões, for menor que 1, as tensões encontram-se no campo elástico. O domínio plástico é alcançado assim que fy(σ) = 1. Valores acima de 1 não são permitidos. O comportamento do modelo é idealmente plástico; ou seja, não há enrijecimento.
Resumo
O módulo de comportamento de material não linear permite a consideração de não-linearidades do material no RFEM 6. Se ativar este módulo nos Dados gerais do modelo, a lista de modelos de materiais expande-se e pode facilmente selecionar o modelo de material não linear de interesse.
Ao trabalhar com modelos de materiais não lineares, o programa realiza sempre um cálculo iterativo. Dependendo do modelo escolhido, este define uma relação diferente entre as tensões e as deformações. A rigidez dos elementos finitos é continuamente ajustada ao longo das iterações até que a relação tensão-deformação seja satisfeita.
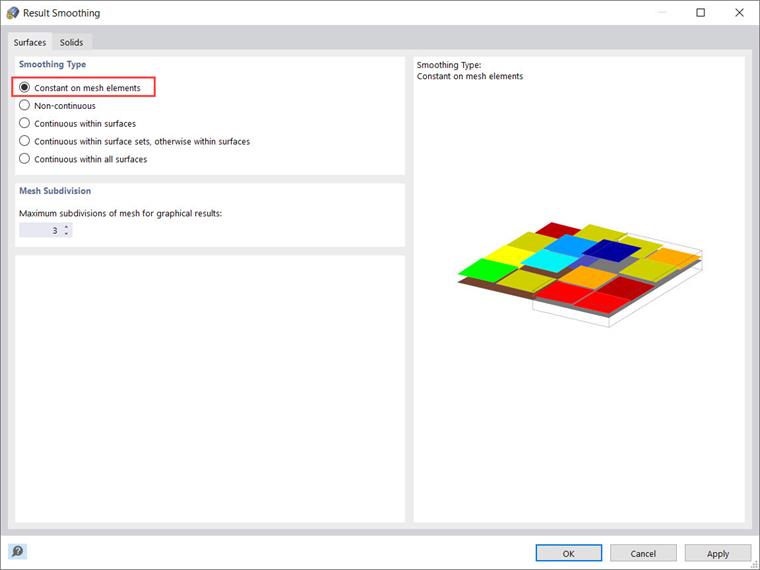
O ajuste é sempre feito para toda uma superfície ou elemento sólido. Portanto, é recomendado sempre usar o tipo de suavização "Constante nos elementos da malha" ao avaliar tensões, conforme mostrado na Imagem 11.