Le module complémentaire Comportement non-linéaire du matériau vous permet de prendre en compte les non-linéarités des matériaux dans RFEM 6. Ce module complémentaire est disponible dans les données de base du modèle comme le montre la figure 1.
Une fois le module complémentaire Comportement non-linéaire du matériau activé, en plus des modèles de matériaux « Isotrope | Linéaire élastique » et « Orthotrope | Linéaire élastique », des options supplémentaires sont disponibles dans la liste (figure 2). Vous pouvez donc choisir parmi les modèles de matériaux suivants :
- Isotrope | Plastique (Barres)
- Isotrope | Plastique (Surfaces/Solides)
- Isotrope | Élastique non linéaire (Barres)
- Isotrope | Élastique non linéaire (Surfaces/Solides)
- Isotrope | Endommagement (Surfaces/Solides)
- Orthotrope | Plastique (Surfaces)
- Orthotrope | Plastique (Solides)
Modèle de matériau Isotrope | Plastique (Barres)
Si vous sélectionnez une des entrées ci-dessus dans la liste déroulante « Modèle de matériau », un nouvel onglet est disponible pour entrer les paramètres du matériau. Ainsi, en sélectionnant le modèle de matériau « Isotrope | Plastique (Barres) », un onglet correspondant apparaît comme le montre la figure 3.
Tout d’abord, vous avez le choix entre les options suivantes pour le type de diagramme :
- Basique
- Bilinéaire
- Diagramme contrainte-déformation
Si vous sélectionnez la première option (« Basique »), le logiciel utilise des valeurs de la base de données des matériaux pour le module d’élasticité E et la limite d’élasticité fy. Veuillez noter qu’il s’agit également d’un modèle de matériau bilinéaire, pour lequel la branche du graphique n’est pas exactement horizontale pour des raisons numériques et possède une petite pente Ep. En revanche, si le diagramme est défini de manière bilinéaire (c’est-à-dire l’option « Bilinéraire »), le programme vous permet d’entrer la valeur de Ep vous-même.
La troisième option disponible (« Diagramme contrainte-déformation ») vous permet de définir des relations plus complexes entre contrainte et déformation. Veuillez noter que dans ce modèle de matériau, le diagramme contrainte-déformation se réfère à la contrainte longitudinale σx. Différents points de limite d’élasticité pour la traction et la compression ne peuvent pas être pris en compte par cette option.
Modèle de matériau Isotrope | Plastique (Surfaces/Solides)
Le modèle de matériau plastique isotrope est également disponible pour les surfaces et les solides. De la même manière que pour le modèle « Isotrope | Plastique (Barres) », un onglet correspondant apparaît lors de la sélection de l’entrée « Isotrope | Plastique (Surfaces/Solides) » dans la liste déroulante. En plus des options pour définir le type de diagramme (les mêmes que pour « Isotrope | Plastique (Barres) »), l'hypothèse de rupture par contrainte doit être sélectionnée (figure 4).
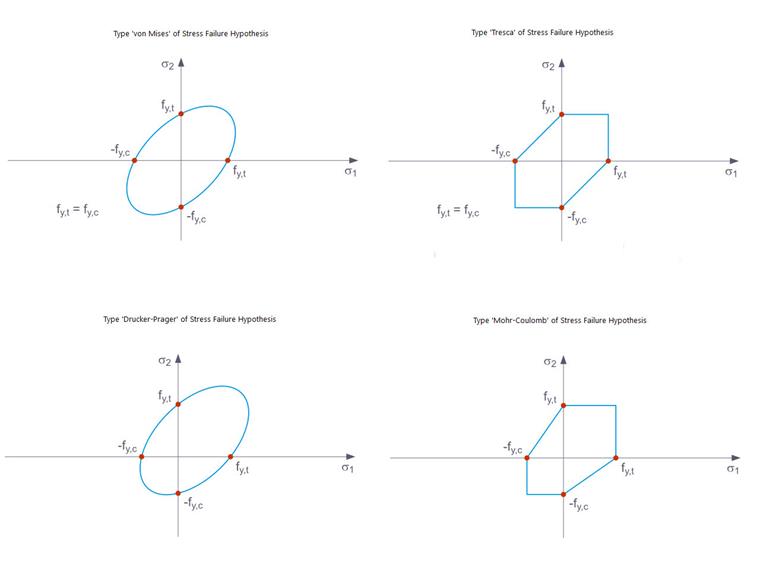
Les hypothèses de rupture par contrainte suivantes sont disponibles dans le menu déroulant :
- von Mises
- Tresca
- Drucker-Prager
- Mohr-Coulomb
Le critère de limite d’élasticité selon von Mises est un cylindre circulaire avec un axe hydrostatique dans l’espace des contraintes principales. Tous les états de contrainte à l’intérieur de cet espace sont entièrement élastiques. Les états de contrainte en dehors de cet espace ne sont pas autorisés. Avec la règle d’écoulement de Tresca, la déformation plastique se produit en raison de la contrainte de cisaillement maximale.
En plus de ces critères d’élasticité, il y a les règles d’écoulement selon Drucker-Prager et Mohr-Coulomb, dans lesquelles la déformation plastique se produit lorsque la contrainte de cisaillement maximale est localement dépassée. Dans le premier cas, il y a une zone de surface avec une frontière lisse dans l’espace des contraintes principales, tandis que le second est une zone de surface avec une frontière non lisse (figure 5).
Modèle de Matériau Isotrope | Non-linéaire-élastique (Barres)
L’onglet pour régler les paramètres du modèle « Isotrope | Élastique non-linéaire (Barres) » est très similaire à celui du modèle de matériau « Isotrope | Plastique (Barres) » (figure 6). En fait, ces modèles se correspondent. La différence entre eux est liée à la distinction générale entre les modèles de matériaux élastiques non linéaires d’un côté, et les modèles plastiques de l’autre.
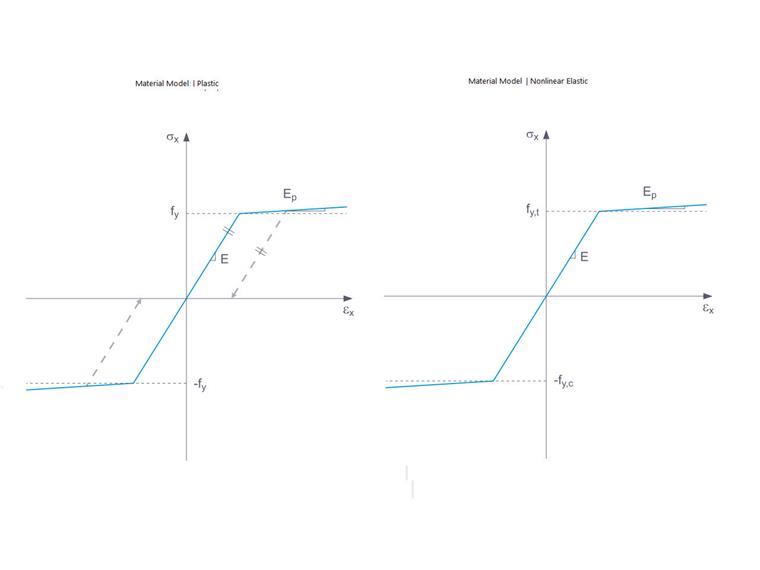
Si un composant structurel avec un matériau élastique non linéaire est effectivement déchargé à nouveau, la déformation revient le long du même chemin et il n’y a plus de déformation lorsque le composant est complètement déchargé. Dans le cas des matériaux plastiques, en revanche, la déformation reste même après que la charge ait été totalement supprimée. La figure 7 montre cela.
Modèle de matériau Isotrope | Non-linéaire élastique (Surfaces/Solides)
La même discussion s’applique à la correspondance entre les modèles de matériaux « Isotrope | Plastique (Surfaces/Solides) » et « Isotrope | Non-linéaire élastique (Surfaces/Solides) ». Les propriétés du modèle doivent être définies de la même manière (figure 8), avec la différence qu’aucune déformation plastique ne reste une fois la charge supprimée.
Modèle de matériau Isotrope | Endommagement (Surfaces/Solides)
Les lois d’élasticité mentionnées précédemment dans l’article sont limitées à la surface de limite d’élasticité dans l’espace des contraintes principales, et leurs règles peuvent uniquement s’appliquer au comportement de matériau purement élastique-plastique. Cependant, de nombreux matériaux n'affichent pas un comportement non linéaire purement symétrique. Afin de simuler le comportement de matériaux exposés à un processus d’endommagement causé par des fissures, un modèle de matériau plus adapté est requis. Le béton, qui présente une résistance à la compression nettement plus élevée que la résistance en traction, correspond à cette définition.
Les fissures qui se produisent dans la zone de traction du matériau réduisent la rigidité du système. Dans le cas du béton armé ou du béton fibré, les armatures absorbent les contraintes de traction.
Pour simuler le comportement de tels matériaux (par exemple, le béton renforcé de fibres d’acier), RFEM 6 comporte le modèle de matériau « Isotrope | Endommagement (Surfaces/Solides) ». Si vous sélectionnez ce modèle de matériau, l’onglet montré dans la figure 9 permet de définir les paramètres du modèle.
Contrairement aux autres modèles de matériaux, le diagramme contrainte-déformation pour ce modèle de matériau n’est pas antimétrique à l’origine. La « Taille de l’élément de référence » contrôle la manière dont la déformation dans la zone de fissure est ajustée à la longueur de l’élément. Avec la valeur par défaut zéro, aucun ajustement n’est effectué. En conséquence, le comportement du béton renforcé de fibres d’acier est modélisé de manière réaliste.
Modèle de matériau Orthotrope | Plastique (Surfaces, Solides) | Modèle Tsai-Wu
Avec le modèle de matériau plastique orthotrope pour surfaces et solides dans RFEM 6, les surfaces et solides avec des propriétés de matériau plastique peuvent être calculés et évalués selon le critère de défaillance de Tsai-Wu. Ce modèle de matériau combine des propriétés plastiques et orthotropes, ce qui permet une modélisation spéciale des matériaux avec des propriétés anisotropes. Ce modèle de matériau peut ainsi être utilisé pour représenter le comportement des plastiques renforcés de fibres ou des panneaux de bois.
Dans ce modèle de matériau, la plage élastique correspond au modèle de matériau "Orthotrope | Élastique Linéaire (Solides)", tandis que pour le domaine plastique, l'écoulement s'applique selon Tsai-Wu. L'Image 10 montre les conditions d'écoulement pour les surfaces (2D) et les solides (3D).
Si la valeur de fy(σ) selon l'équation de Tsai-Wu, état de contrainte plane, est inférieure à 1, les contraintes sont dans la plage élastique. Le domaine plastique est atteint dès que fy(σ) = 1. Les valeurs supérieures à 1 ne sont pas autorisées. Le comportement du modèle est idéalement plastique ; c'est-à-dire qu'il n'y a pas de raidissement.
Résumé
Le module complémentaire Comportement non-linéaire du matériau permet de prendre en compte les non-linéarités des matériaux dans RFEM 6. Si vous activez ce module complémentaire dans les Données de base du modèle, la liste des modèles de matériaux s'élargit et vous pouvez facilement sélectionner le modèle de matériau non linéaire d’intérêt.
Lorsque vous travaillez avec des modèles de matériaux non linéaires, le logiciel effectue toujours un calcul itératif. En fonction du modèle choisi, il définit une relation différente entre les contraintes et les déformations. La rigidité des éléments finis est continuellement ajustée au cours des itérations jusqu'à ce que la relation contrainte-déformation soit satisfaite.
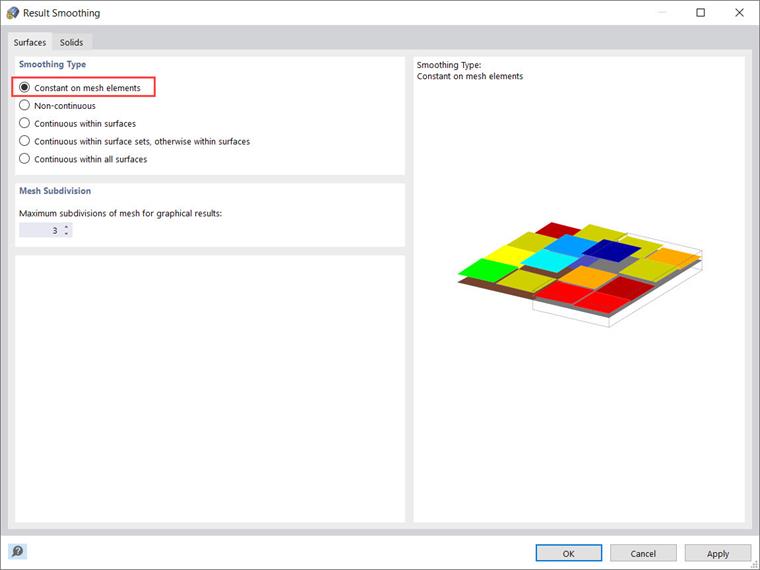
L’ajustement est toujours fait pour un ensemble complet de surfaces ou de solides. Il est donc recommandé d’utiliser toujours le type de lissage "Constant sur éléments de maillage" lors de l'évaluation des contraintes, comme indiqué dans l'Image 11.