Воздействия
Оценка усталости обычно требуется только для тех компонентов опорной конструкции крана, которые подвержены колебаниям напряжения от вертикальных крановых нагрузок ( [2] , раздел 9.1 [3]). В сопроводительном примечании к стандарту говорится, что колебания напряжений из-за боковых нагрузок крана обычно незначительны. Однако их следует учитывать при проектировании соединений или при большем количестве многократных ускорений и торможений. Таким образом, возникают только вертикальные колесные нагрузки, которые должны быть изменены соответствующими динамическими коэффициентами в соответствии с [3] , раздел 2.12.1 (7).
Коэффициенты динамического воздействия на вертикальные колесные нагрузки:
φжир, 1 = (1 + φ1 )/2
φжир, 2 = (1 + φ2 )/2
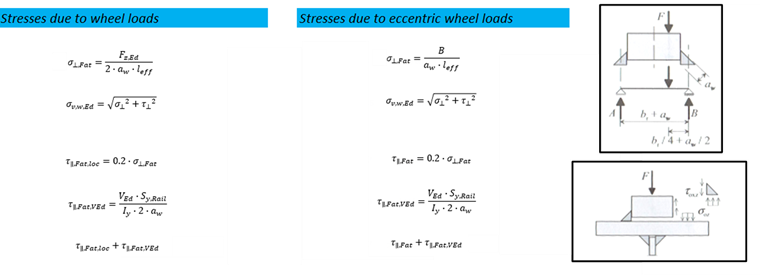
Напряжения от колесных нагрузок
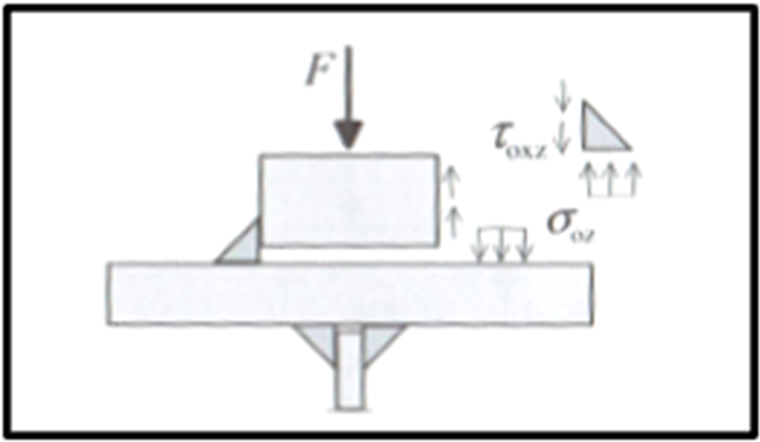
В отличие от предельного состояния по прочности, в случае расчета на усталость напряжения относятся к угловой ветви сварного шва. Необходимо учитывать напряжения σ из-за нагрузки на колесо, а также локальные и общие касательные напряжения из-за поперечной силы в соответствии с [4] , раздел 5 (6).
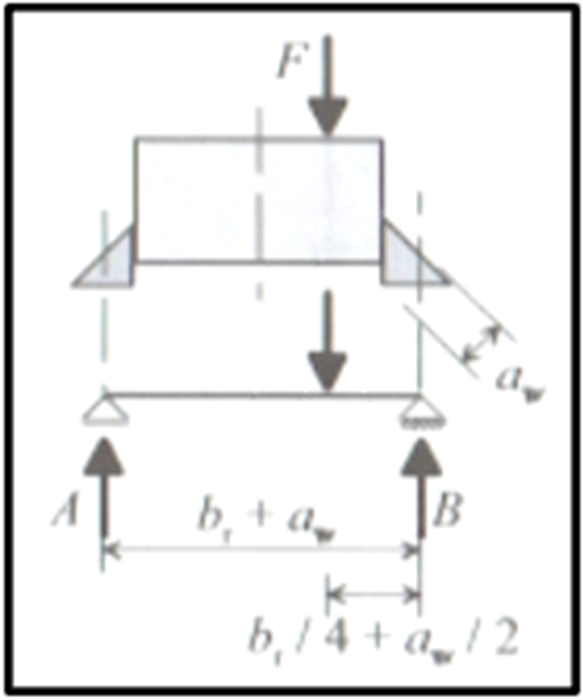
Согласно [2], расчет на усталость сварных швов должен учитывать эксцентричную нагрузку на колесо ¼ ширины головки рельса от класса повреждения крана S3 ([2], раздел 9.3.3 [1]). Следовательно, если кран на подкрановом пути имеет класс повреждения ≥ S3, необходимо определить местные напряжения от колесных нагрузок на верхнем фланце, включая компонент от эксцентриковой колесной нагрузки. Простая инженерная модель для определения повышенной нагрузки на колесо представлена в [1].
Для расчета касательных напряжений местное напряжение сдвига может быть определено с использованием 20% вертикального напряжения, вызванного нагрузкой на колесо, в соответствии с [2], раздел 5.7.2 (1). Кроме того, должны применяться общие касательные напряжения из-за разницы поперечных сил кранового прохода ∆V.
Как для расчета нагрузок на колеса, так и для определения характеристик поперечного сечения, высота изношенного подкранового рельса может быть установлена на уровне 12,5% в соответствии с [2], раздел 5.6.2 (3). Эффективная длина приложения нагрузки рассчитывается так же, как и при расчете по предельному состоянию.
Расчет предельного состояния по усталости
Расчет на усталость выполняется с использованием спектра диапазонов напряжений, полученного в результате расчета конструкции. Диапазоны напряжений являются результатом общих напряжений следующим образом:
∆σ = σмакс - σмин
∆τ = τмакс - τмин
Для местных напряжений диапазоны напряжений - это соответствующие максимальные значения, поскольку минимальные значения равны 0.
Диапазон напряжений, эквивалентных повреждению
Задача состоит в том, чтобы преобразовать многоуровневый спектр напряжений в одноуровневый спектр с одинаковыми повреждениями и определить результирующий диапазон эквивалентных напряжений, связанных с 2 ⋅ 10 6 циклами напряжений.
Используя нормированные кривые S ‑ N (наклон m = 3 для продольных напряжений и наклон m = 5 для касательных напряжений) и максимальное количество рабочих циклов в зависимости от класса повреждения крана согласно [3], таблица 2.11, можно получить следующие формулы быть выведенным.
Расчет диапазона напряжений, эквивалентных повреждению:
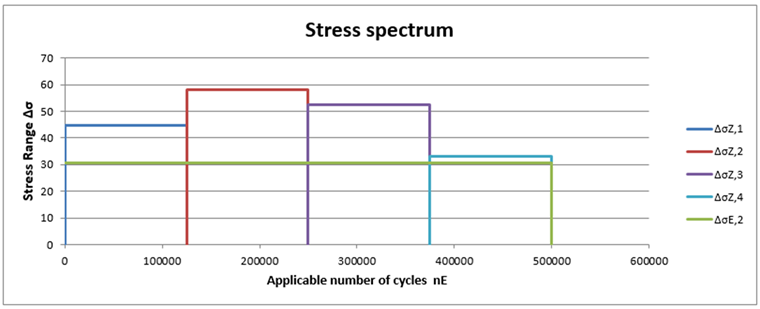
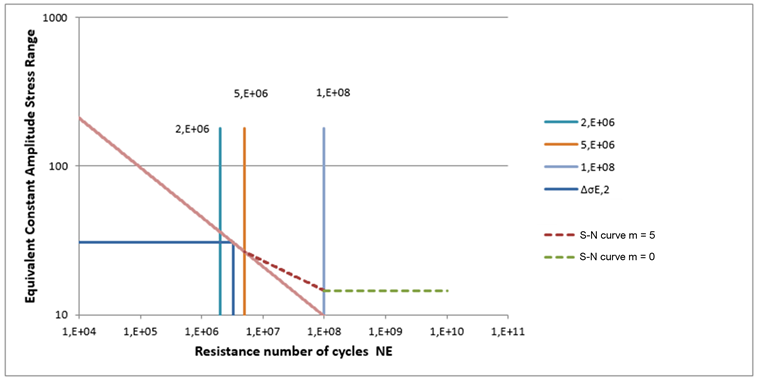
Графическое представление с использованием выбранной кривой S ‑ N дает следующую диаграмму:
Теперь, используя детали конструкции, сварной шов и соответствующую категорию надреза (Δσc и Δτc ), можно выполнить окончательный расчет. Детали конструкции приведены в [4], таблицы 8.1–8.10. Таблица 8.10, в частности, включает некоторые детали подкрановой балки.
Частные коэффициенты зависят от запланированных интервалов проверок и являются результатом [4], Таблица 3.1 и [2], NA/Таблица NA.3: NA.3:
Согласно [4], раздел 5 (6), взаимодействие не выполняется для расчета сварного шва.