Einwirkungen
Ein Ermüdungsnachweis ist grundsätzlich nur für Bauteile der Kranbahn erforderlich, die Spannungsänderungen infolge vertikaler Radlasten ausgesetzt sind ([2], Kap. 9.1 (3)). In der zugehörigen Anmerkung der Norm ist weiterhin ausgeführt, dass Spannungsänderungen infolge Seitenlasten in der Regel vernachlässigbar sind. Diese sollten jedoch für die Bemessung von Verbindungen oder bei hoher Anzahl von wiederkehrenden Beschleunigungs- und Bremskräften berücksichtigt werden. Daraus ergeben sich nur vertikale Radlasten, die nach [3], Kap. 2.12.1 (7) mit den entsprechenden dynamischen Faktoren zu modifizieren sind.
Dynamische Faktoren zur Modifizierung der vertikalen Radlasten:
φfat,1 = (1 + φ1) / 2
φfat,2 = (1 + φ2) / 2
Spannungen infolge Radlasten
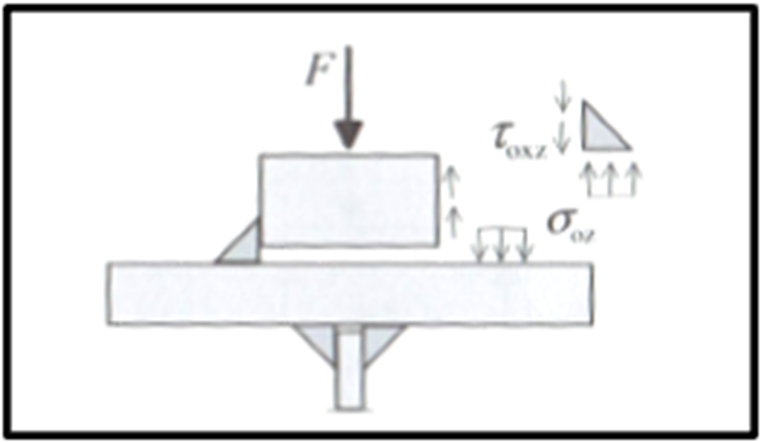
Im Gegensatz zum Nachweis im Grenzzustand der Tragfähigkeit beziehen sich die Spannungen im Ermüdungsnachweis auf die Winkelschenkel der Schweißnaht. Es sind σ-Spannungen infolge Radlast sowie lokale und globale Schubspannungen aus der Querkraft zu berücksichtigen [4], Kap. 5 (6).
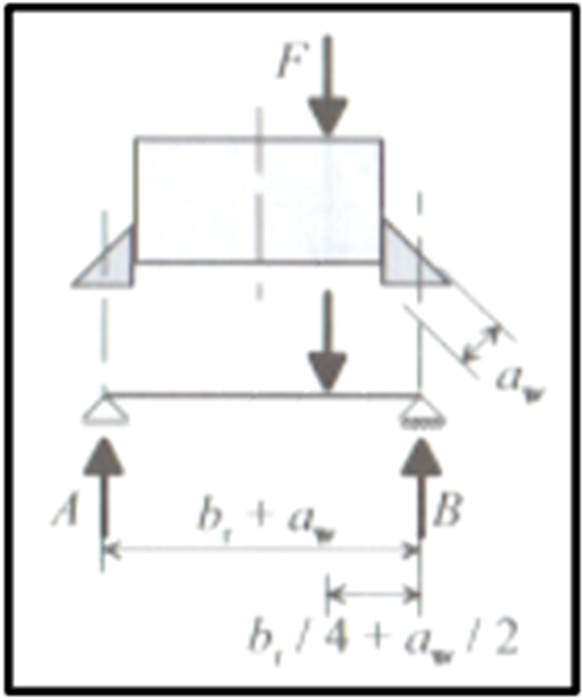
Die Besonderheit im Ermüdungsnachweis der Schweißnähte nach [2] ist die Berücksichtigung des exzentrischen Radlastangriffes von ¼ der Schienenkopfbreite ab einer Schadensklasse des Kranes von S3 ([2], Kap. 9.3.3 (1)). Sofern also der Kran auf der Kranbahn eine Schadensklasse ≥ S3 aufweist, müssen die lokalen Spannungen infolge Radlasten am Obergurt inklusive einem Anteil aus exzentrischer Radlast ermittelt werden. In [1] wird ein einfaches Ingenieurmodell für die Ermittlung der erhöhten Radlast dargestellt.
Für die Berechnung der Schubspannungen darf die lokale Schubspannung nach [2], Kap. 5.7.2 (1) mit 20 % der vertikalen Spannung aus Radlast ermittelt werden. Weiterhin sind die globalen Schubspannungen aus der Querkraftdifferenz einer Überfahrt ∆V anzusetzen.
Sowohl bei der Berechnung der Radlastspannungen als auch für die Ermittlung der Querschnittswerte darf die abgenutzte Schienenhöhe mit 12,5 % angesetzt werden [2], Kap. 5.6.2 (3). Die effektive Lasteinzugslänge berechnet sich analog der Vorgehensweise im Nachweis der Grenzzustand der Tragfähigkeit.
Nachweise im Grenzzustand der Ermüdung
Der Ermüdungsnachweis wird mit den aus der statischen Berechnung ergebenden Spannungsschwingbreiten geführt. Spannungsschwingbreiten aus globalen Beanspruchungen ergeben sich wie folgt:
∆σ = σmax - σmin
∆τ = τ max - τmin
Für lokale Beanspruchungen ergeben sich die Spannungsschwingbreiten zu den entsprechenden Maximalwerten da die Minimalwerte 0 sind.
Schadensäquivalente Spannungsschwingbreite
Die Aufgabe besteht darin, ein mehrstufiges Spannungskollektiv in ein einstufiges Kollektiv mit der gleichen Schädigung zu überführen und die daraus resultierende schadensäquivalente Spannungsschwingbreite bezogen auf 2 ∙ 106 Spannungsspiele zu ermitteln.
Unter Verwendung der normierten Wöhlerlinien (Steigung m = 3 für Längsspannungen und Steigung m = 5 für Schubspannungen) und der maximalen Anzahlen an Arbeitsspielen, abhängig von der Schadensklasse des Kranes nach [3], Tab. 2.11, können folgende Formeln hergeleitet werden.
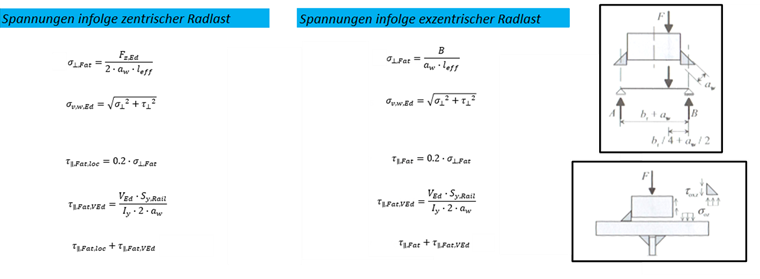
Berechnung der schadensäquivalenten Spannungsschwingbreiten:
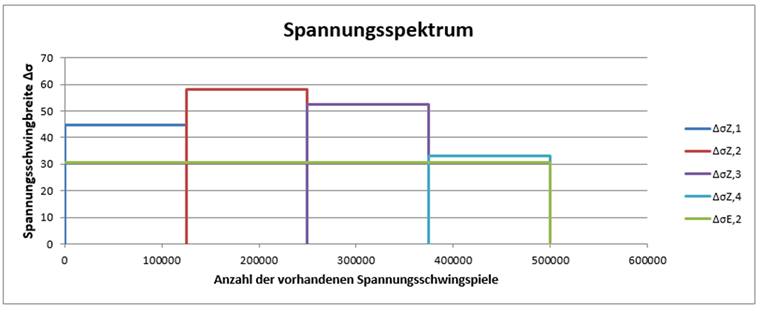
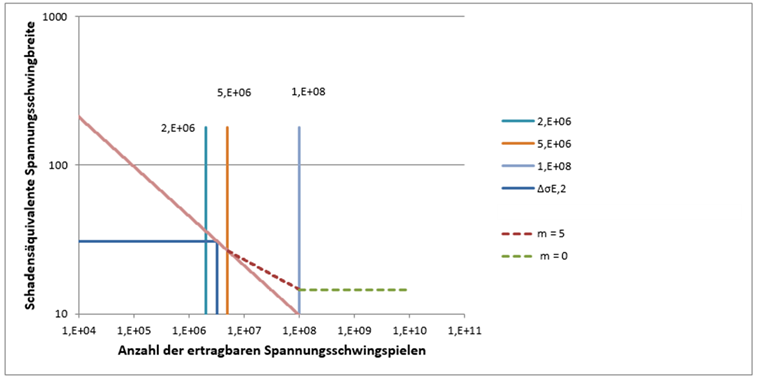
Anhand der gewählten Wöhlerlinie ergibt sich folgende grafische Darstellung:
Nun kann mithilfe des nachzuweisenden Konstruktionsdetails, in diesem Fall der Schweißnaht, und dem damit verbundenen Kerbfall (∆σc und ∆τc) der abschließende Nachweis geführt werden. Die Konstruktionsdetails sind in [4], Tab. 8.1 - 8.10 dargestellt, besonders Tabelle 8.10 behandelt einige Details des Kranbahnträgers.
Die Teilsicherheitsbeiwerte sind von den geplanten Inspektionsintervallen abhängig und ergeben sich aus [4], Tab. 3.1 und [2], NA/Tab. NA.3:
Eine Interaktion ist nach [4], Kap. 5 (6) für die Nachweise der Schweißnähte nicht zu führen.