Коэффициенты критической нагрузки, относящиеся к напряжению
В [1] приведено следующее уравнение (раздел 10, уравнение 10.6) для чисто аналитического определения коэффициента критической нагрузки панели с потерей устойчивости:
Как видно, соотношения напряжений, а также коэффициенты критической нагрузки определяются отдельно для отдельных компонентов напряжения или должны быть известны. Коэффициенты критической нагрузки можно определить путем пересчёта критических напряжений потери устойчивости пластин. Как это определить, уже было описано в следующей технической статье:
Таким образом, для отдельных компонентов напряжения мы получим следующие соотношения:
Данный метод особенно подходит для неусиленных или продольно усиленных панелей с потерей устойчивости, для которых применяются соответствующие значения потери устойчивости из [2] или [3].
Расчет с помощью метода конечных элементов
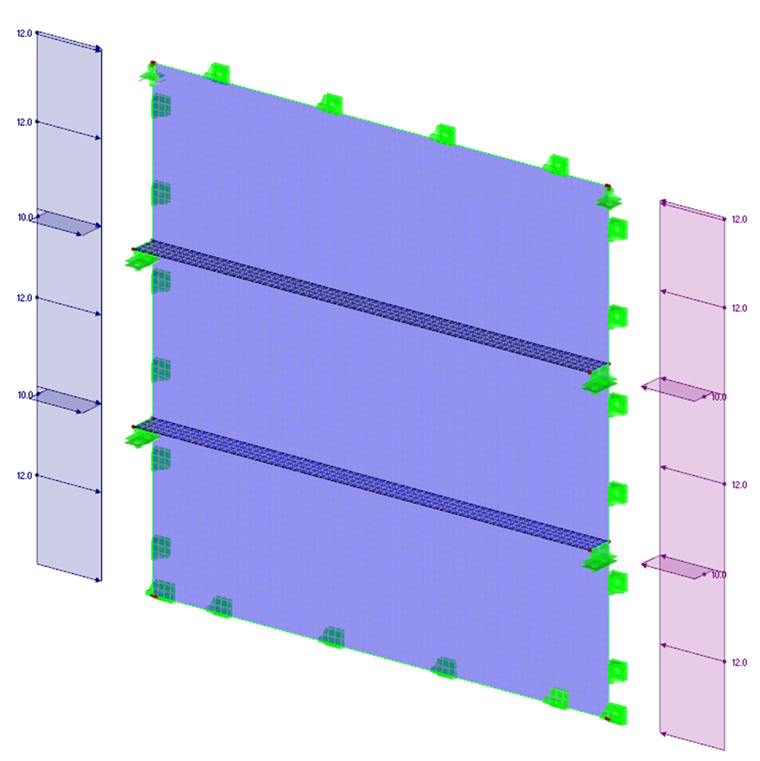
Если панель с потерей устойчивости сильно укреплена продольными и поперечными элементами жесткости, то для определения критической нагрузки на всю конструкцию следует применить расчет по МКЭ. В качестве основы необходимо применить модель поверхности и учесть все граничные условия (например, опоры по краям, геометрическое положение и нагрузку на элемент жесткости, а также граничные напряжения). Для определения по LBA применяется упругая работа материала. Следующий пример показывает моделирование продольно усиленной пластины с потерей устойчивости в RFEM.
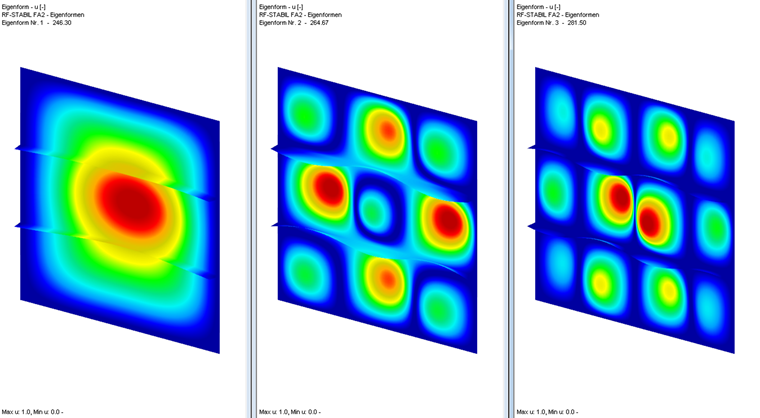
Для определения коэффициента критической нагрузки затем применяется дополнительный модуль RF-STABILITY. При выборе собственной формы необходимо учитывать общий отказ системы.
Первая Собственная форма в нашем примере демонстрирует общую потерю устойчивости при изгибе и, следовательно, ее следует считать определяющей. Тем не менее, в некоторых случаях для расчета могут быть применимы более высокие формы колебаний. Таким образом, коэффициент критической нагрузки можно рассчитать как для всех компонентов напряжения, так и отдельно (только один компонент напряжения на загружение).
Автономная программа PLATE-BUCKLING позволяет выполнить полный расчёт потери устойчивости по методу приведенного напряжения, включая автоматическое определение собственных значений для каждой составляющей напряжения.
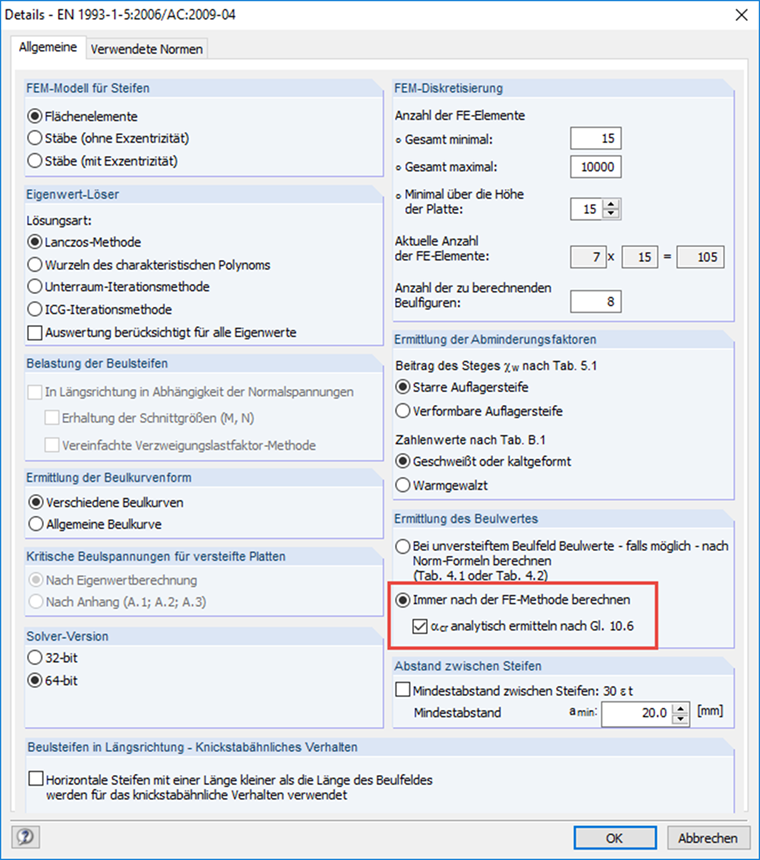
Коэффициент критической нагрузки в расчёте потери устойчивости
Теперь можно определить либо отдельные коэффициенты критической нагрузки, либо аналитически рассчитать общий коэффициент критической нагрузки с помощью уравнения 10.6, приведенные в [1], или применить их непосредственно из расчета по МКЭ. В некоторых случаях аналитическое решение можно считать консервативным. Поэтому PLATE-BUCKLING предлагает следующие возможности.