Critical Load Factors Relating to Stress
[1] provides the following equation (Sec. 10, Eq. 10.6) for a pure analytical determination of the critical load factor of a buckling panel:
This shows that, in addition to the stress ratios, the critical load factors must also be determined separately or already known for the individual stress components. You can determine the critical load factors by recalculating the critical plate buckling stresses. The determination of this has already been described in this technical article:
Thus, the following relations result for the individual stress components:
This method is particularly suitable for unstiffened or longitudinally stiffened buckling panels that apply the corresponding buckling values from [2] or [3].
Calculation Using Finite Element Analysis
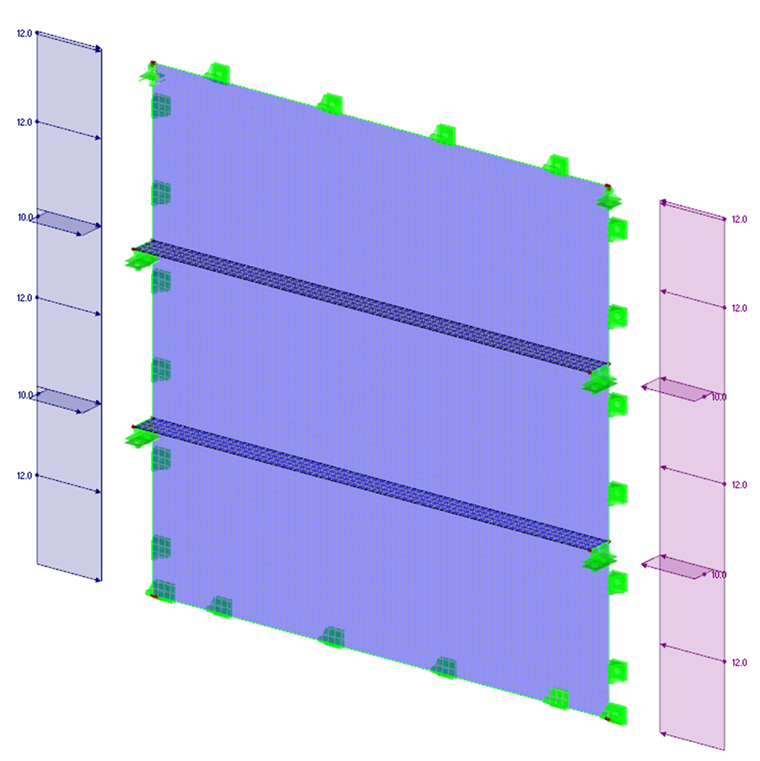
If there is a strongly stiffened buckling panel with longitudinal and transverse stiffeners, the FEM calculation should be used to determine the critical load on the entire structure. As a basis, you should apply a surface model and consider all boundary conditions (for example, supports at the edges, the geometrical position and stiffener loading, as well as boundary stresses). For the determination according to LBA, elastic material behavior is applied. The following example shows the modeling of a longitudinally stiffened buckling plate in RFEM.
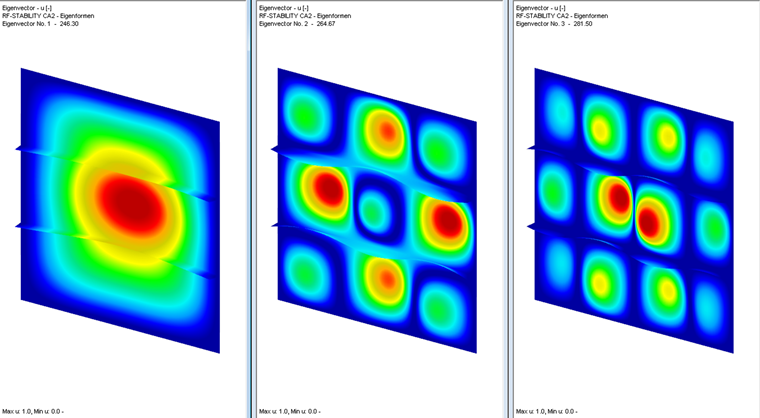
The RF-STABILITY add-on module is used to determine the critical load factor. When selecting a mode shape, the global system failure must be taken into account.
The first mode shape in this example shows global buckling and is, therefore, to be regarded as governing. However, higher mode shapes may be relevant for design in some cases. Thus, the critical load factor can be calculated for all stress components as well as separately (only one stress component per load case).
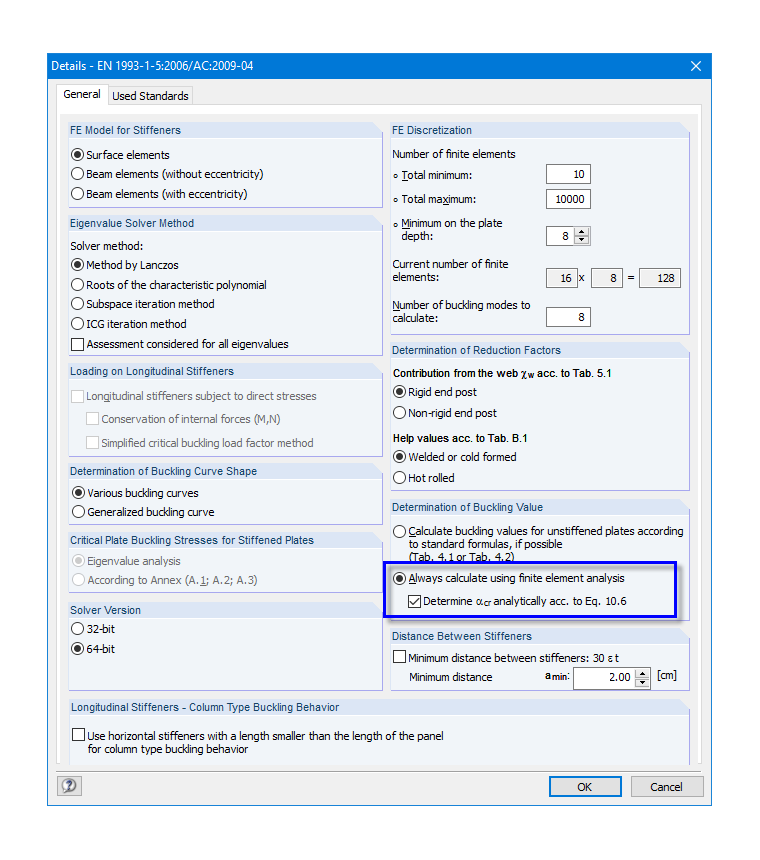
The PLATE-BUCKLING standalone program allows you to perform a complete buckling analysis using the reduced stress method, including the automatic determination of eigenvalues for each stress component.
Critical Load Factor in Buckling Analysis
Now, it is possible to either determine the individual critical load factors and analytically calculate the total critical load factor using Eq. 10.6 provided in [1], or to use them directly from the FEM calculation. In some cases, the analytical solution may be regarded as conservative. Therefore, PLATE-BUCKLING provides the following options.